
- •Рівномірний розподіл
- •Розподіл « xи-квадрат»
- •Показовий розподіл
- •Математичне очікування
- •Рівняння виду
- •Диференціальні рівняння виду , що не містять шуканої функції
- •Загальний розв’язок лінійного однорідного рівняння з постійними коефіцієнтами
- •Линейные неоднородные уравнения с постоянными коэффициентами. Общее решение. Метод подбора.
- •Чисельні методи розв’язання диференціальних рівнянь
- •Розв’язання диференціальних рівнянь за допомогою функції odesolve в Mathcad
- •Метод Ейлера для диференціальних рівнянь першого порядку в MathCad
- •Рішення систем диференціальних рівнянь в Mathcad.
- •Рішення диференціальних рівнянь методом Рунге-Кутти
- •Розв’язання диференціальних рівнянь вищих порядків
- •Кореляційний аналіз
- •Лінійна інтерполяція.
- •Інтерполяція сплайнами
-
Головною характеристикою безперервно розподіленої випадкової величини є щільність імовірності. У загальному випадку вона дорівнює похідної функції розподілу й розуміється як відношення ймовірності влучення випадкової величини у вузьку околицю певного значення до розміру цієї околиці. За допомогою щільності ймовірності виводяться всі найважливіші характеристики безперервної випадкової величини, такі як дисперсія або математичне очікування.
-
Біномінальний розподіл
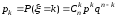
В
MathCad для обчислення щільності ймовірності
й функції розподілу випадкової величини,
що має біномінальний розподіл, призначена
функція dbinom(k, n, p) і pbinom(k, n, p), значення
яких – відповідно
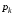 й
й
 .
.
-
Пуасоновский розподіл.
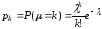
В
MathCad для обчислення щільності ймовірності
й функції розподілу випадкової величини,
що має пуасоновский розподіл, призначені
функції dpois (k,
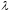 )
і ppois (k,
)
і ppois (k,
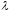 ),
значення яких – відповідно
),
значення яких – відповідно
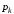 й
й
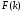 .
.
-
Геометричний розподіл
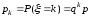
В
MathCad для обчислення плотності ймовірності
й функції розподілу випадкової величини,
що має геометричний розподіл, призначені
функції dgeom (k, p) і pgeom (k, p), значення яких
– відповідно
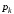 й
й
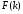 .
.
-
Гіпрегеометричний розподіл
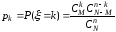
В MathCad немає убудованих функцій для обчислення щільності ймовірності й функції розподілу випадкової величини, що має гіпергеометричний розподіл. Ці функції можна визначити по наведеним вище формулах.
-
Від’ємний біномінальний розподіл
Крім звичайного, в Mathcad є функції й від’ємного біномінального розподілу (negative binomial distribution). Цей розподіл має лише теоретичне значення й застосовується, наприклад, для визначення кількості невдалих експериментів до n-го успішного експерименту в ряді незалежних випробувань Бернуллі, якщо ймовірність успіху дорівнює р, або для підрахунку якісних виробів, відібраних до появи n-го ушкодженого виробу.
Задаються функції негативного биноминального розподілу за допомогою кореня nbinom і відповідних приставок. Наприклад, pnbinom(k,n,p) — функція ймовірності для розглянутого розподілу.
-
Рівномірний розподіл
Прочитайте й законспектуйте!
Найбільш простим безперервним розподілом є рівномірний розподіл, тобто розподіл що має однакову щільність на всьому проміжку визначення.
Випадкові
величини, розподілені за рівномірним
законом, мають кінцеві границі інтервалів
зміни. Знаючи їх, зовсім не важко з
обліком нормування вивести формулу
щільності ймовірності ( ):
):
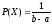
В Mathcad даній формулі відповідає функція dunif(x,a,b) (від англ. uniform distribution -рівномірний розподіл).
Функція рівномірного розподілу задається в Mathcad як punif(x,a,b), де а й b - границі інтервалу зміни випадкової величини (див. малюнок нижче). Загальну ж її формулу можна знайти, використавши символьне інтегрування:

-
Щільність імовірності нормально розподіленої випадкової величини описується формулою:
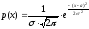
де
a - це математичне очікування випадкової
величини,
 -
її середньоквадратичне відхилення.
-
її середньоквадратичне відхилення.
В
Mathcad щільність нормального розподілу
обчислюється за допомогою убудованої
функції dnorm(x,
 ,a)
(дивіться малюнок нижче).
,a)
(дивіться малюнок нижче).
Інтегрування
щільності ймовірності дає функцію
розподілу. В Mathcad обчислення, пов'язані
з її застосуванням, можна робити завдяки
наявності спеціальної убудованої
функції pnorm(x, ,a).
Використовуючи функцію розподілу, можна
визначати, яка ймовірність того, що
випадкова величина прийме значення з
певного проміжку.
,a).
Використовуючи функцію розподілу, можна
визначати, яка ймовірність того, що
випадкова величина прийме значення з
певного проміжку.
-
Розподіл « xи-квадрат»
Якщо
n випадкових величин розподілені за
нормальним законом, причому для всіх
математичне очікування дорівнює 0, а
середньоквадратичне відхилення - 1, то
сума їхніх квадратів розподілена за
законом
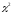 ,
щільність імовірності якого описується
наступною формулою (x>0):
,
щільність імовірності якого описується
наступною формулою (x>0):
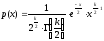
Як видно з наведеної формули, описане розподіл залежить тільки від одного параметра k - числа ступенів волі (k= n-1, де n - кількість випадкових величин). При більших k розподіл «хі-квадрат» наближається до нормального. У статистиці розглянутий розподіл застосовується для обчислення інтервалу, у якому може змінюватися дисперсія випадкової величини. Доведено, що границі довірчого інтервалу для дисперсії можна визначити як
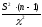
де S2 — вибіркова дисперсія, n — кількість елементів у вибірці, χ2— коефіцієнт, що обчислюється виходячи з «хі-квадрат» розподілу. Традиційно ці коефіцієнти беруться зі спеціальних таблиць при ймовірностях, рівні ймовірності виходу випадкової величини за межі інтервалу. Обчислюються ж ці граничні ймовірності як (1+α)/2 і (1– α)/2 (де α — довірча ймовірність). По суті, коефіцієнти χ2 є квантилями відповідного розподілу, так що для того, щоб вирішити задачу про довірчий інтервал для дисперсії в Mathcad, зовсім не потрібно звертатися до спеціальних таблиць. Для їхнього обчислення просто потрібно скористатися убудованою функцією квантилей qchisq(p,d), де p - довірча ймовірність, d - кількість ступенів волі.
-
Розподіл Стьюдента застосовується для рішення дуже багатьох статистичних зaдач, однак найбільше важливо його використання для обчислення довірчого інтервалу математичного очікування нормально розподілених даних.
У статистикці доведено, що довірчий інтервал для математичного очікування можна оцінити як

де n - об'єм вибірки, S - «виправлене» середньоквадратичне відхилення, t - квантиль розподілу Стьюдента. Таблиці із критичними точками для останнього можна знайти не тільки в підручниках по статистиці, але й у будь-якій допомозі з виконання лабораторних робіт (у які він визначається за рівнем значимості (залежить від техніки виконання вимірів) і кількості ступенів волі (тобто від кількості паралельних вимірів)).
Відповідне значення можна одержати й за допомогою функції квантилей qt(р,d), де р - довірча ймовірність, d - кількість ступенів волі випадкової величини.
