Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Украинская инженерно-педагогическая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ряжена.doc

Скачиваний:

Добавлен:

16.11.2018

Размер:

725.5 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Вихідні дані асинхронного двигуна.

Числа фаз обмоток статору і ротору , тобто рівні

Лінійна напруга на фазі статору .

Потужність, кВт

Pn=10;

Номінальна частота обертання, об/хв

nn=1460;

Частота обертання магнітного поля n₀, об/хв

n0=1500;

Перевантажувальна здатність

lam=3.0;

ПАРАМЕТРИ СТАТОРУ

Коефіціент потужності номінальний та при холостому ході

cosfnom=0.87; cosf0=0.24;

Номінальний струм статору, А

I1n=28.4;

Струм намагнічування при холостому ході, А

I10=19.2;

Активний опір фази статору, Ом

r1=0.415;

Індуктивний опір фази статору , Ом

x1=0.465;

ПАРАМЕТРИ РОТОРУ

Номінальна ЕРС фази ротору (ЕРС на кільцях розімкненого ротору), , В

Ernom=200;

Номінальний струм , А

I2n=35.4;

Активний опір фази ротору , Ом

r2=0.132;

Індуктивний опір фази статору, , Ом

x2=0.27;

Момент інерції, , кг/м²

J=0.3;

Номер схеми включення на динамічне гальмування згідно до табл 1

ind=4;

Розрахунок. Розрахунок.

Частина1. Параметри заступної схеми асинхронного двигуна та статичні механічні характеристики

Вид заступної схеми приведений на рисунку.

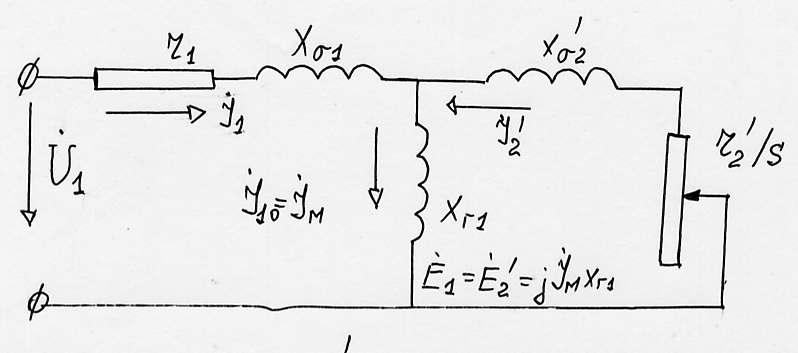
Рисунок 1 – Заступна схема асинхронного двигуна при його живленні від джерела напруги

Коефіцієнт приведення опорів вторинної обмотки до первинної і параметри схеми :

(1)

де - числа фаз статору і ротору, а оскільки - вимірюється міх кільцями ротору і є лінійною, то є лінійною ЕРС фази статору.

kr=(0.95*380/Ernom)^2

ke=sqrt(kr)

kr =

3.2580

ke =

1.8050

Опори заступної схеми. При обчисленні опору намагнічуючого контуру прийнята фазна ЕРС статору як

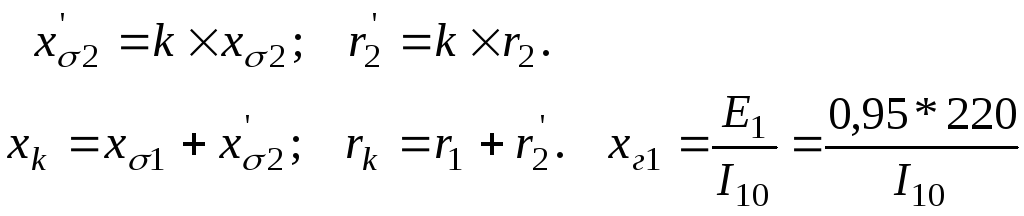(2)

x21=kr*x2

r21=kr*r2

xk=x1+x21

x0=0.95*220/I10

Номінальний опір ротора

Ом (3)

R2nom=Ernom/I2n/sqrt(3)

Механічна характеристика асинхронного двигуна традиційно представляється у вигляді залежності моменту від ковзання двигуна М(s).

Ковзання , навпаки ,.

sn=(n0-nn)/n0

x21 =

0.8797

r21 =

0.4301

xk =

1.3447

x0 =

10.8854

Вид характеристики визначається формулою Клосса

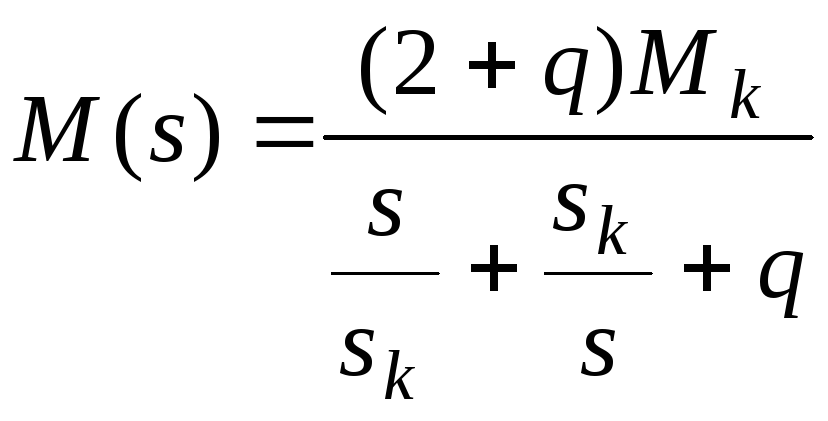. (4)

Де s_k - критичне ковзання

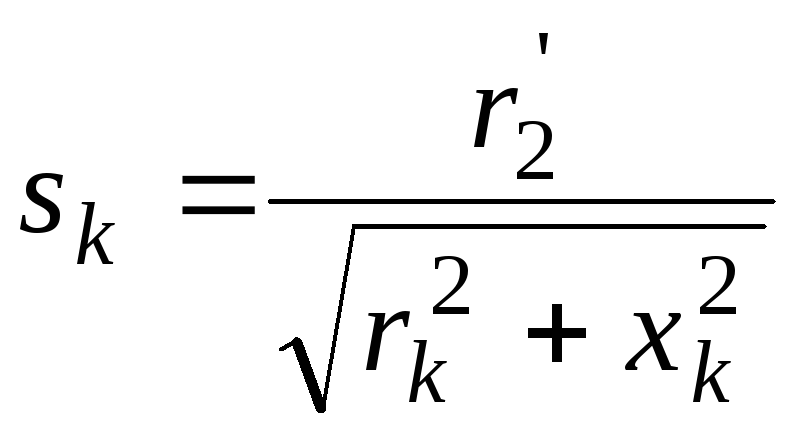(5)

sk=r21/sqrt(r1^2+xk^2)

R2nom =

3.2619

Мк - критичний момент, Нм

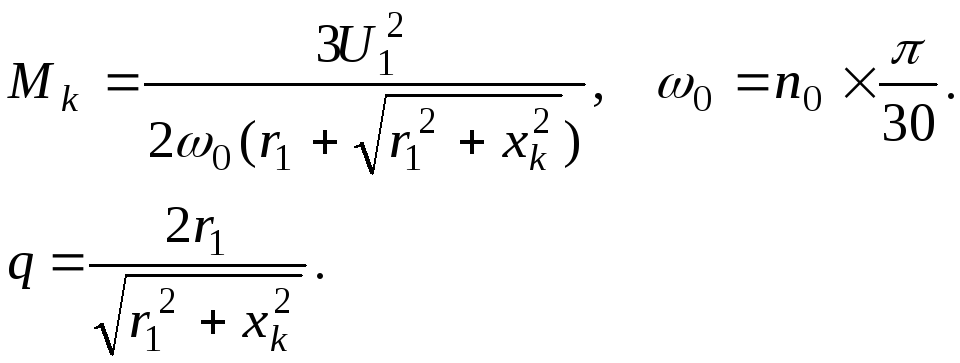(6)

w0=n0*pi/30;

q=2*r1/sqrt(r1^2+xk^2)

q =

0.5898

sn =

0.0267

U1f=220;

Mk=3*U1f^2/2/w0/(r1+sqrt(r1^2+xk^2))

Mk =

253.6347

sk =

0.3056

(Перевірка перевантажувальної здатності:

l=Mk/(Pn*1e+3*30/pi/nn)

l =

3.8778

sk =

0.3056

порівняти із табличною

lam nk =

1.0416e+003

По формулах слід побудувати таблиці значень характеристик (природню та штучні), а самі характеристики зображувати графічно на міліметрівці. При побудові реостатної характеристики слід врахувати опір роторного ланцюга . Прийнято

Механічні характеристики

s=[-2:0.03:2];

ni=n0.*(1-s);

% Природня характеристика

M=(2+q)*Mk./(s/sk+q+sk./s);

I_2=U1f./sqrt((r1+r21./s).^2+xk^2);

% Характеристика при снижении напряжения 0,7U1f

U1i=0.7*U1f;

Mki=3*U1i^2/2/w0/(r1+sqrt(r1^2+xk^2));

Miu=(2+q)*Mki./(s/sk+q+sk./s);

I_2iu=U1i./sqrt((r1+r21./s).^2+xk^2);

% Реостатная характеристика

r_2i=r21+0.3*R2nom* kr;

ski=r_2i/sqrt(r1^2+xk^2);

Mir=(2+q)*Mk./(s/ski+q+ski./s);

I_2ir=U1f./sqrt((r1+r_2i./s).^2+xk^2);

kharM1=figure;

figure(kharM1);

kharI1=figure;

plot (M, ni,'k-', Miu, ni, 'r-',Mir, ni,'r--')

grid on

Xlabel(' m, h m')

ylabel('n, ob/xv')

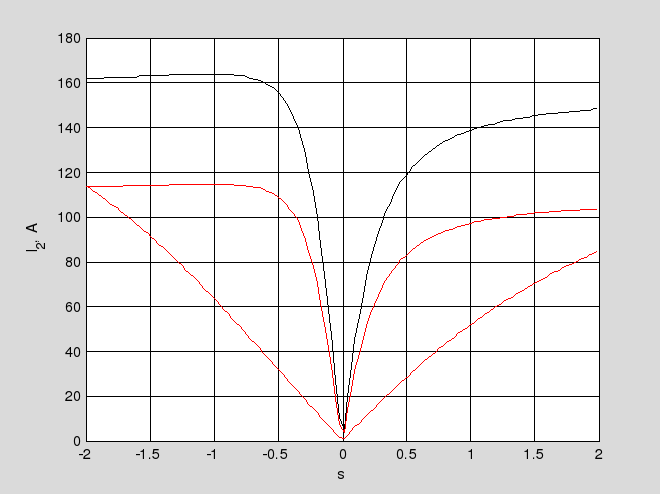
Електромеханічні характеристики

figure(kharI1);

plot (s, I_2,'k-', s, I_2iu, 'r-', s, I_2ir, 'r--')

grid on

ylabel(' I_2, A')

Xlabel('s')

xmu =

Columns 1 through 6

24.4427 24.4427 23.0639 21.0348 18.8021 16.7652

Columns 7 through 10

15.0685 13.6668 12.4929 11.4975

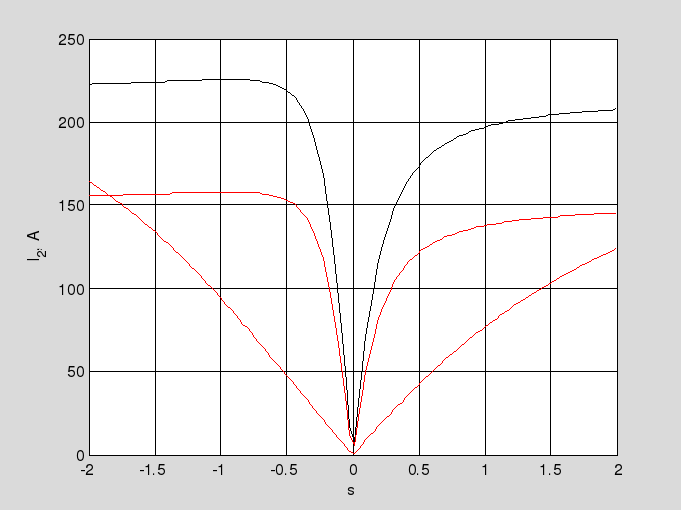
На обох графіках такі позначення - природня харакетристика на графіку – суцільна чорна лінія, суцільна червона лінія – характеристика при зниженні напруги статору до 0,7 U_1ф, а переривчаста червона лінія – реостатна характеристика при введені в фазу ротора додаткового опору .

При механічна характеристика близька до лінійної залежгності, , а в області великих ковзань має гіперболічний характер . При момент набуває максимальних значень, причому в руховому режимі () відповідне значення критичного моменту , ніж в генераторному режимі (). Різниця моментів оцінюється кількісно

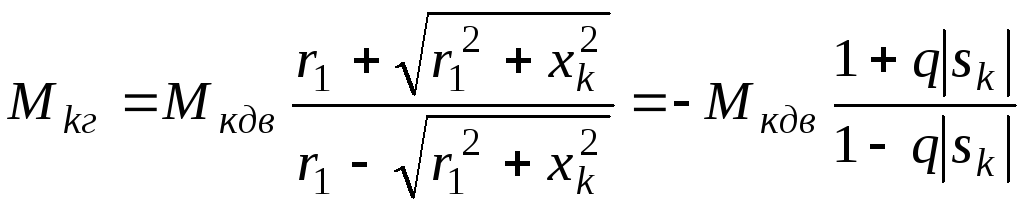(7)

Пояснення виду механічної характеристики асинхронного двигуна полягає в аналізі залежностей моменту двигуна від струму ротора і потоку двигуна ().

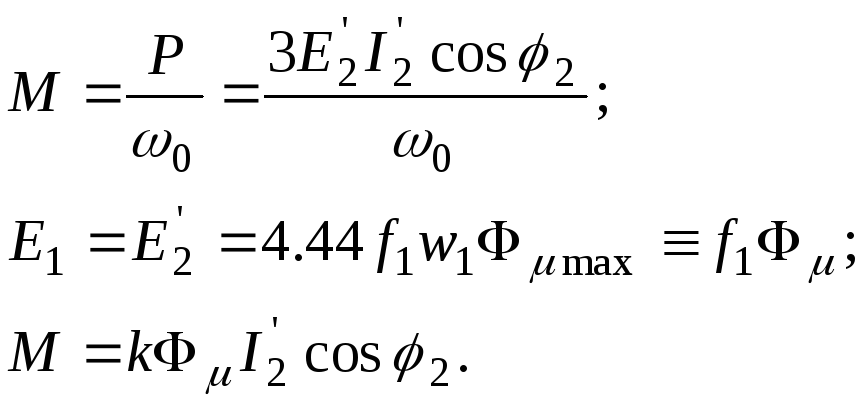(8)

Т. ч. залежність моменту від ковзання визначається характером зміни потоку, струму ротора і при змінах ковзання.

Розглядаючи залежність можна переконатися, що в області рухового режиму струм ротора монотонно зростає, прагнучи при до асимптоти . В генераторному режимі легко виявляється максимум , відповідний до , причому струм ротора при прагне до тієї ж асимптоти, що і в руховому режимі. Подібний вид має і залежність струму статора ( у режимі хх ).Залежність від ковзання можна отримати за допомогою схеми заміщення, як: 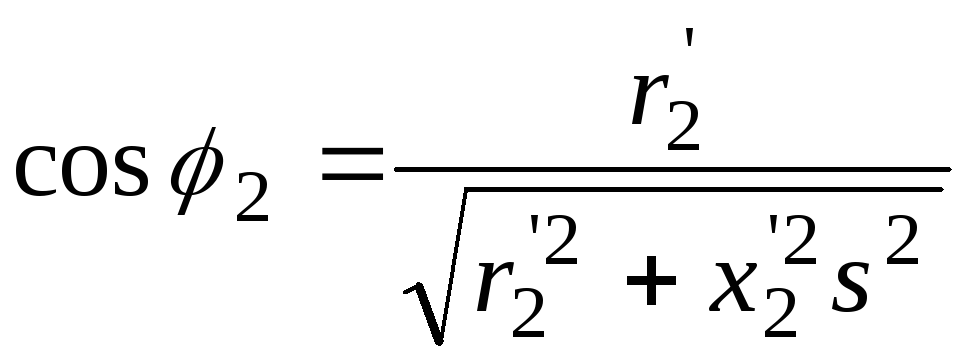. Отже, при зростанні модуля ковзання монотонно убуває, прагнучи при до нуля.

Якщо прийняти, що магнітний потік можна дійти висновку, що момент двигуна при малих ковзаннях, де міняється повільно, повинен зростати при збільшенні ковзання приблизно пропорційно струму . В області ж великих ковзань, навпаки, струм  і змінюється мало, тоді момент долджен знижуватися приблизно за тим же законом, що і . Максимум моменту настає при ковзанні, якому відповідає умова .

Насправді ж ЕРС і магнітний потік двигуна при роботі в руховому режимі у міру зростання навантаження і зв"язаного з ним падіння напруги в колі статора знижуються. Це зниження носить монотонний характер і додається до розглянутого вище впливу змін , не міняючи характеру залежності . Наявність максимуму струму в кривій в області генераторного режиму пояснюється тим, що у зв'язку із зміною фази струму статора і падіння напруги на опорі ЕРС двигуна і потік в області малих ковзань продовжують зростати і перевищують значення, відповідні ідеальному холостому ходу. При великих ковзаннях визначальним стає падіння на опорі , тут ЕРС і потік знижуються аналогічно зниженню ЕРС і потоку в руховому режимі роботи. Цим обумовлені максимум ЕРС і потоку в генераторному режимі і відповідний йому максимум струму ротора, і, як наслідок, максимум моменту в генераторному режимі більший, ніж в руховому.

Частина 2. Характеристики асинхронного двигуна в режимах динамічного гальмування

З живленням АД від джерела струму тісно пов'язане режим динамічного гальмування АД. Цей режим обумовлений живленням обмотки статора постійним струмом, при цьому магнітне поле статора нерухоме і ротор гальмується в постійному магнітному полі. Постійний струм статора при цьому не пов'язаний індуктивно з ротором. Динамічне гальмування двигуна з самозбудженням є простим, економічним і ефективним способом збільшення діапазону регулювання швидкості при спуску вантажів, тому його застосування інтенсивно розширюється.

Схема включення АД на динамічне гальмування:

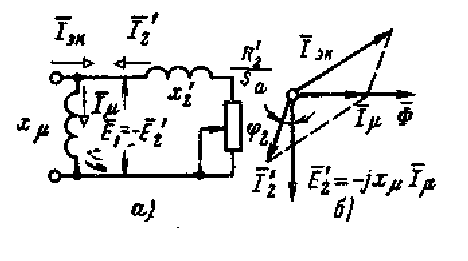
Рисунок 2 - Включення АД на динамічне гальмування, еквівалентна заступна схема режиму і відповідна їй векторна діаграма

При розрахунку живлення обмотки статора постійним струмом Iп приводиться до еквівалентної схеми живлення від трифазного струму I_1экв. Умовою такого эквивалентирования є рівність МДС, cоздаваемых постійним струмом Iп при вибраній схемі з'єднань обмотки статора при гальмуванні і еквівалентним змінним струмом I₁.

МДС системи трифазного струму I_1экв визначається відомою з теорії машин змінного струму формулою

, відповідно, МДС при живленні від джерела постійного струму і включенні за заданою схемою гальмування прирівнюється до F_экв, звідки виходять співвідношення I_1экв, приведені в таблиці 1:

Таблиця 1 - Можливі схеми включення обмоток статора АД на динамічне гальмування

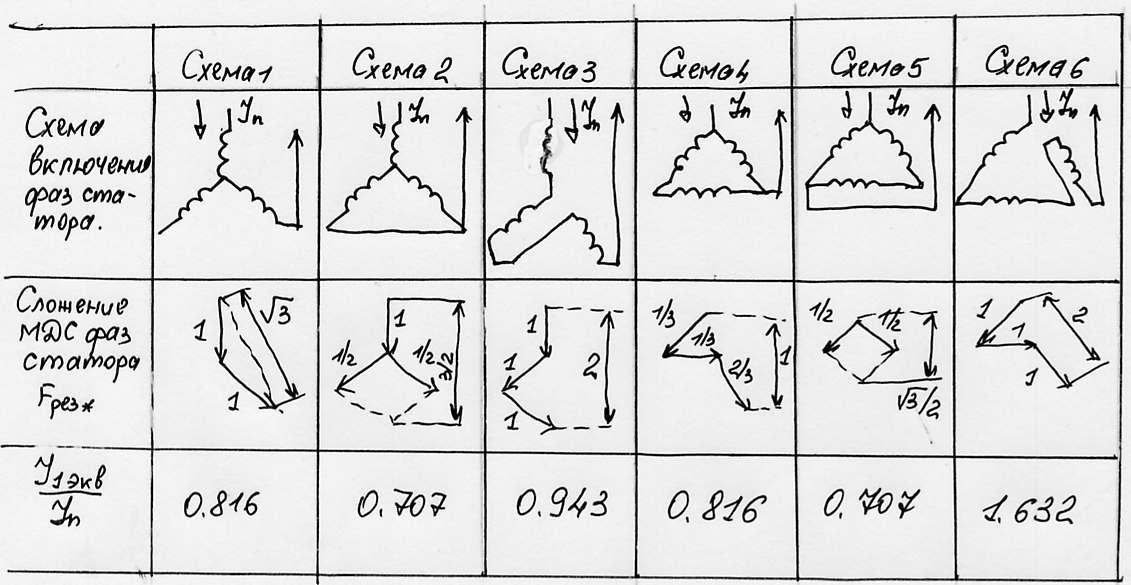
Слід мати на увазі, що при динамічному гальмуванні

а основні співвідношення згідно до схеми рис.3 та векеторної діаграми рис.2 мають вигляд

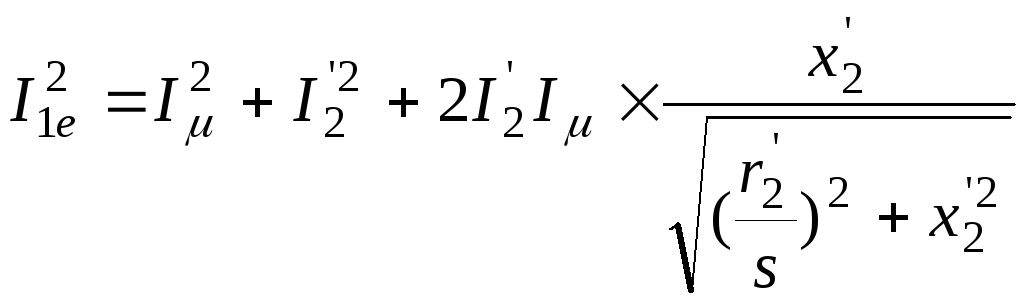звідки

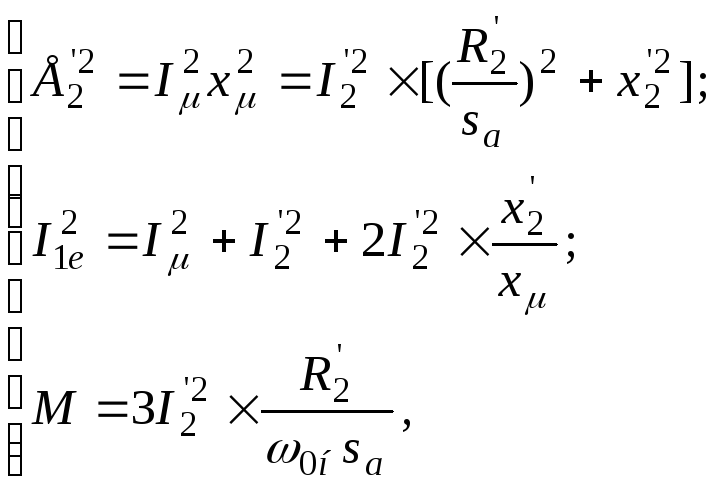(9)

Тому на базі формул (9) будується подальший алгоритм розрахунку процесу.

Подальший алгоритм розрахунку вірізняється тим, що як вихідний аргумент приймається не зміна ковзання, як раніше, а зміна насичення контура Г- образної схеми заміщення (її вхідного намагнічуючого опору), що має місце при динамічному гальмуванні, а потрібні нам значення ковзання, струму і моменту розраховуються.

Критичний момент та криртичне ковзання при динамічному гальмуванні визначаються як

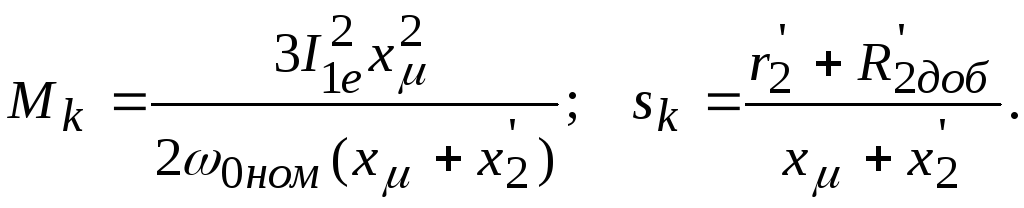
Заступна схема при динамічному гальмуванні (живленні двигуна від джерела струму)

Рисунок 3 – Заступна схема асинхронного двигуна при його живленны выд джерела струму

Алгоритм розрахунку режиму динамічного гальмування

Універсальна характеристика намагнічування АД у в.о. → → →

→ → → →

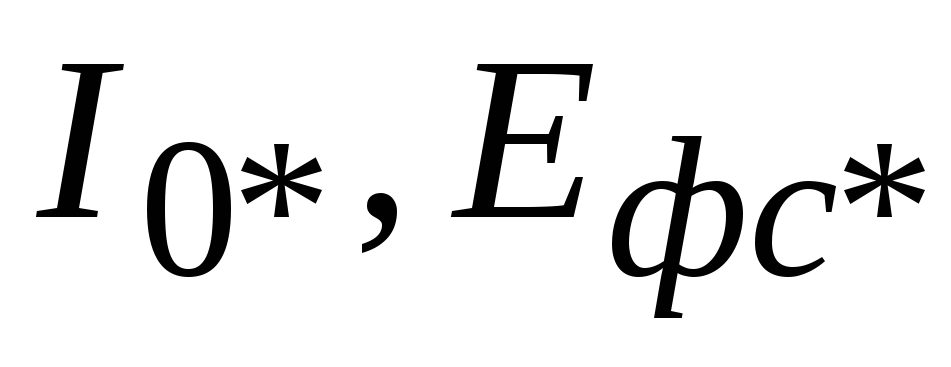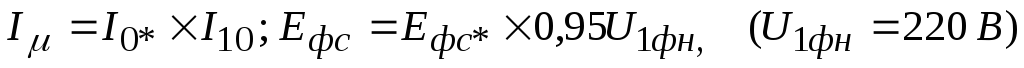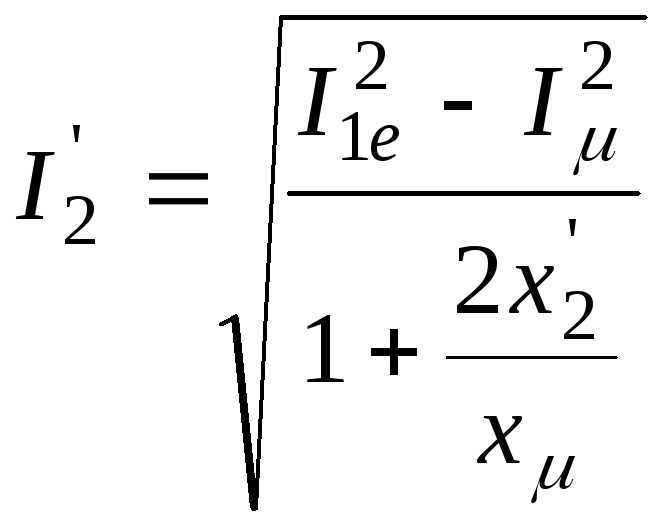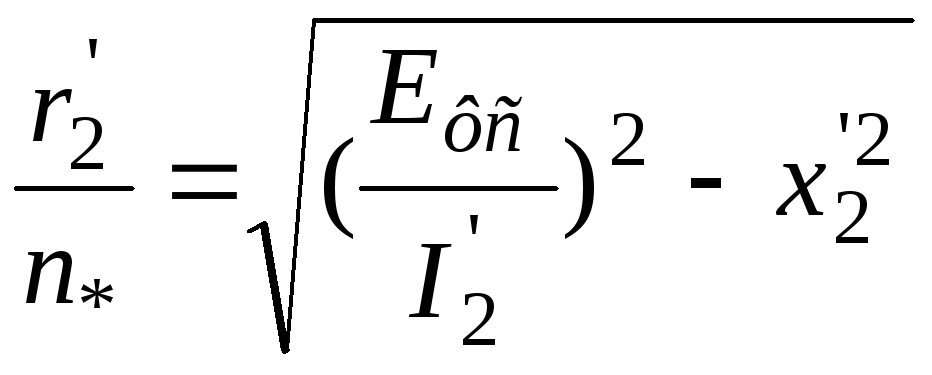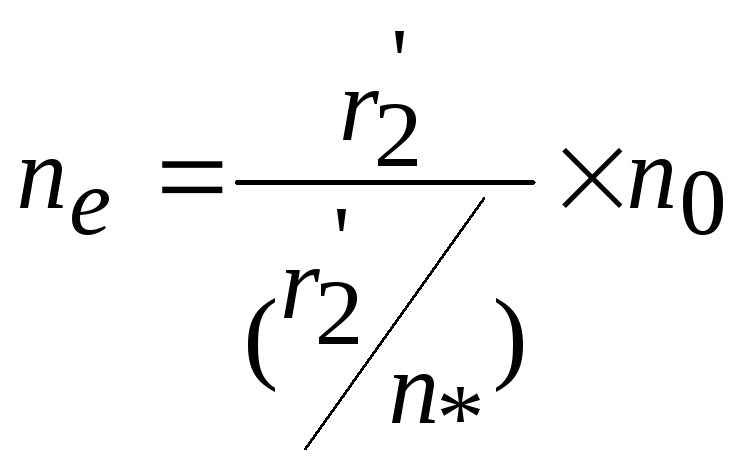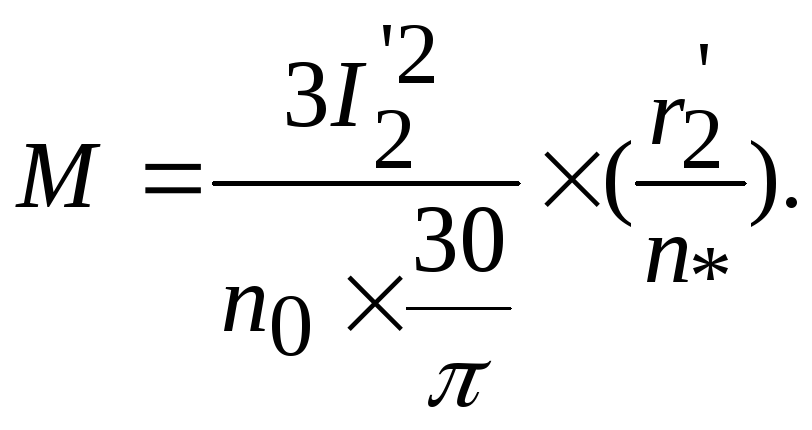→ (10)

Примусове динамічне гальмування із величиною постійного струму 3I₁₀ .

Згідно до табл. 1 введіть номер схеми включення обмотки статору на динамічне гальмування

switch ind

case 1

ki=0.816

case 2

ki=0.707

case 3

ki=0.943

case 4

ki=0.816

case 5

ki=0.707

case 6

ki=1.632

otherwise

disp('невірно задано номер схеми')

end

ki =

0.8160

R11 =

1.3203

I_1экв визначається за таблицею еквівалентування (табл. 1) для заданої схеми включення на динамічне гальмування

Еквівалентний струм при динамічному гальмуванні, А

I1e=ki*3*I10

I1e =

47.0016

Нижче наведено табличний алгоритм розрахунку динамічного гальмування для розглядуваного випадку

Таблиця 2

Общие данные для любых токов возбуждения				Данные для принятого постоянного тока возбуждения
Кривая намагничивания		Вспомогат. расчеты

1	2	3	4	5	6	7	8	9	10
0,2	0,26
0,4	0,52
0,6	0,736
0,8	0,895
1,0	1,0
1,2	1,07
1,4	1,122
1,6	1,163
1,8	1,196
2,0	1,223

Стовпці 1 і 2 таблиці є універсальною кривою намагнічування АД у в.о.

Характеристика намагничівання у в.о

.I_0=[0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2];

E_f1=[0.26 0.52 0.736 0.895 1 1.07 1.122 1.163 1.196 1.223];

Стовпці 3 і 4 Намагнічуючий струм в А та ЕРС фази статору у В

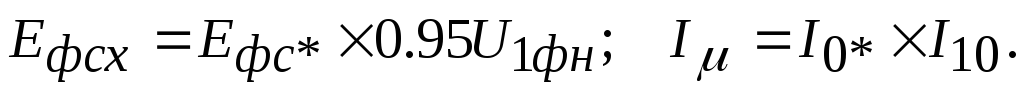
де I₁₀ – номинальний струм намагнічування статору,

U1n=380;

Imu=I10.*I_0

Efc=0.95*U1n.*E_f1

Imu =

Columns 1 through 6

3.8400 7.6800 11.5200 15.3600 19.2000 23.0400

Columns 7 through 10

26.8800 30.7200 34.5600 38.4000

Efc =

Columns 1 through 6

93.8600 187.7200 265.6960 323.0950 361.0000 386.2700

Columns 7 through 10

405.0420 419.8430 431.7560 441.5030

Стовпець 5 – реактивний опір намагнічуючого кола Х_г1

Опір намагнічуючого контуру, який відповідає характеристиці намагнічування xmu=Efc./Imu

sk1 =

3.0567

Стовпець 6

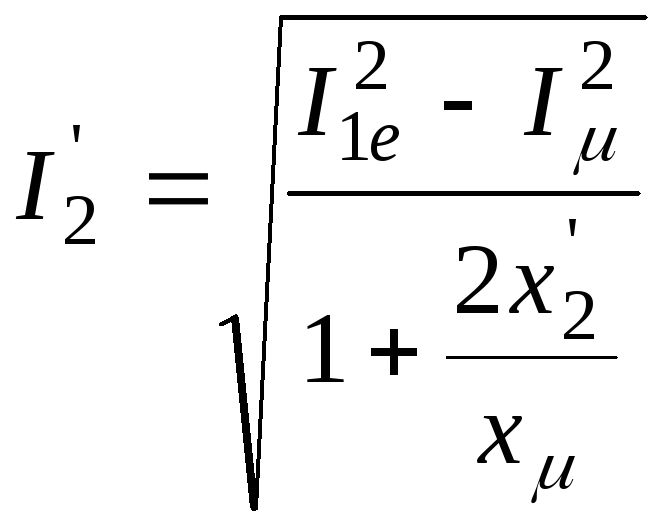
z1=I1e^2.-Imu.^2

z1 =

1.0e+003 *

Columns 1 through 6

2.1944 2.1502 2.0764 1.9732 1.8405 1.6783

Columns 7 through 10

1.4866 1.2654 1.0148 0.7346

z2=1+2*x21./xmu

z2 =

Columns 1 through 6

1.0720 1.0720 1.0763 1.0836 1.0936 1.1049

Columns 7 through 10

1.1168 1.1287 1.1408 1.1530

I_2dt=sqrt(z1./z2)

I_2dt =

Columns 1 through 6

45.2445 44.7861 43.9235 42.6722 41.0247 38.9733

Columns 7 through 10

36.4855 33.4830 29.8244 25.2409

Стовпець7

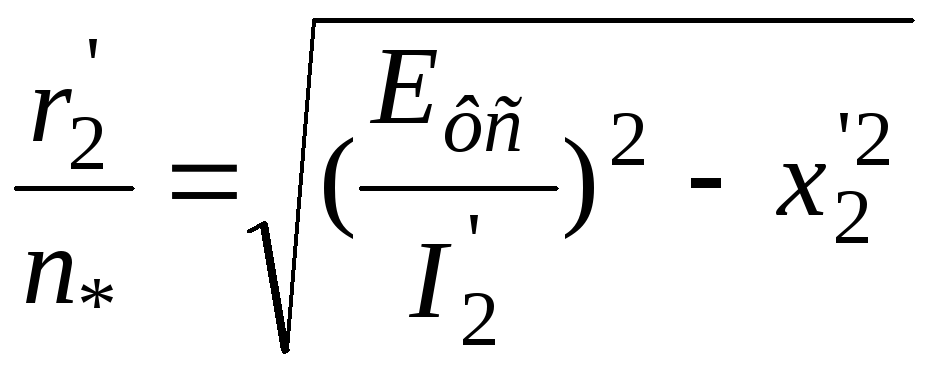
r_2n=sqrt((Efc./I_2dt).^2-x21^2)

r_2n =

Columns 1 through 6

1.8788 4.0981 5.9848 7.5203 8.7555 9.8720

Columns 7 through 10

11.0665 12.5081 14.4499 17.4695

Стовпці 8 Швидкість на природній характеристиці у об/хв

ne=r21./r_2n.*n0

ne =

Columns 1 through 6

343.3574 157.4105 107.7886 85.7800 73.6782 65.3450

Columns 7 through 10

58.2918 51.5737 44.6432 36.9267

Столвпeць 9 момент у Нм:

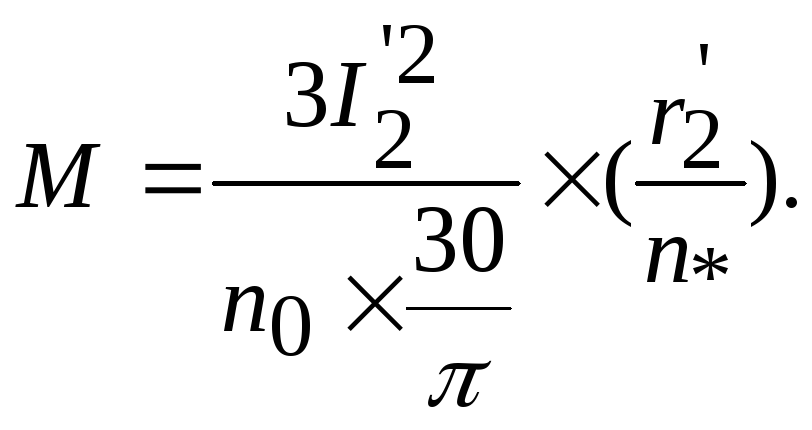
Mdt=-3.*(I_2dt).^2.*r_2n./w0

Mdt =

Columns 1 through 6

-73.4523 -156.9907 -220.5169 -261.5328 -281.4318 -286.3793

Columns 7 through 10

-281.3546 -267.8189 -245.4753 -212.5639

Динаміка асинхронного приводу (без урахування електричної постійної часу), визначається відповідно до основного рівняння приводу як:

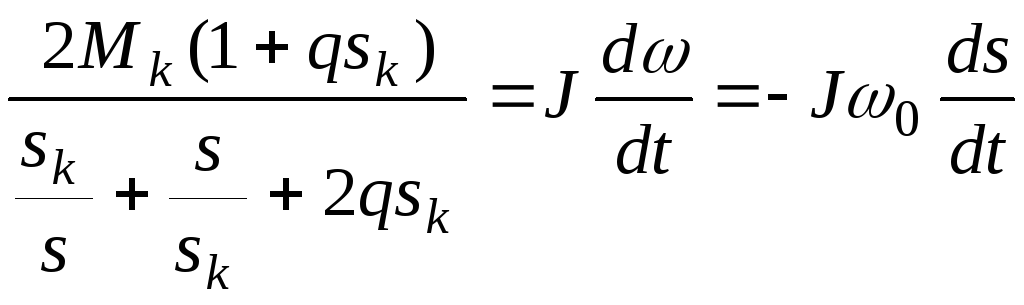Звідки визначається закон зміни швидкості при перехідному процесі

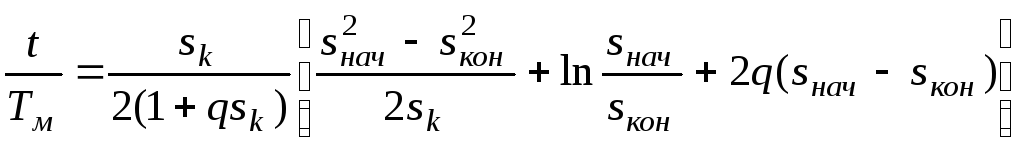
– механічна постійна часу. Час протікання перехідного процесу (гальмування і ін.) виявляється відповідно до функції критичної величини ковзання sk, тобто параметрів АД. Ця чудова властивість АД знаходить своє пояснення в самому виді механічної характеристики АД, що має екстремум в критичній точці. Існує мінімум часу протікання перехідного процесу при варіації параметрів роторного кола.