
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§6. Пределы функций на бесконечности.
Примеры.
-
y= f(х)=arctg(x), Х=(
 ,
+
,
+ ).
).
При х y
y ,
при х
,
при х +
+ y
y .
.
-
y= f(х)=
 , Х=(
, Х=( ,
+
,
+ ).
y
).
y 0
при х
0
при х .
.
О таких функциях в этом параграфе и пойдёт разговор.
Определение.
Пусть f(х) имеет стандартную область определения Х, и пусть множество Х неограниченно сверху (Х неограниченно снизу).
Говорят,
что число L является пределом функции
f(х) при х +
+ (соответственно, при х
(соответственно, при х )
и пишут
)
и пишут
 f(х)=L
(соответственно,
f(х)=L
(соответственно,
 f(х)=L),
если
f(х)=L),
если
 (Г)2
(К)2
(Г)2
(К)2
 {хn}
{хn}
 :
:
 0
0
 D>0
D>0
 х
(х
х
(х Х,
х>D):
Х,
х>D):
│f(х)- L│<
 f(хn)=L
(соотв. х<D): │f(х)-
L│<
f(хn)=L
(соотв. х<D): │f(х)-
L│<
Определения (Г)2 и (К)2 эквивалентны.
(Г)2 и (К)2 обладают всеми свойствами пределов функций, арифметическими и другими.
Замечание.
Неограниченная
сверху область определения Х функции
f(х) может содержать
промежуток [a,
+ )
или (a,
+
)
или (a,
+ ),
но необязательно, а неограниченная
снизу область определения Х функции
f(х) - промежутки (
),
но необязательно, а неограниченная
снизу область определения Х функции
f(х) - промежутки ( ,
b]
или (
,
b]
или ( b),
и тоже необязательно.
b),
и тоже необязательно.
Например.
-
f(х)=
 ,
Х=(
,
Х=( ,
0)
,
0) (0,
+
(0,
+ ).
). -
f(х)=
 ,
Х=
,
Х= ,
,
 (n+1))
(n+1))
§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
-
f(х)=
 ,
Х=(
,
Х=( ,
0)
,
0) (0,
+
(0,
+ ).
При х
).
При х 0
f(х)
0
f(х) +
+
-
f(х)=х3, Х=(
 ,
+
,
+ ).
При х
).
При х f(х)
f(х) ,
при х
,
при х +
+ f(х)
f(х) +
+ .
.
Определение.
Пусть f(х) имеет стандартную область определения Х, точка хо лежит внутри или является концом одного из промежутков, образующих Х.
Говорят,
что f(х) стремится к + (к
(к
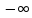 )
при х
)
при х хо
и пишут
хо
и пишут
 f(х)=
+
f(х)=
+ (соответственно,
(соответственно,
 f(х)=
f(х)= ),
если
),
если
(Г)3 (К)3

 {хn}
{хn}

 Е>0
Е>0
 >0
>0
 х
(х
х
(х Х,
х
Х,
х хо,
│x - хо│<
хо,
│x - хо│< ):
):
f(х)>Е (соотв.
f(х)< Е)
Е)
 f(хn)=
+
f(хn)=
+
(соотв.
 f(хn)=
f(хn)= )
)
Определения (Г)3 и (К)3 эквивалентны. (Г)3 и (К)3 обладают всеми свойствами пределов функций.
Аналогично определяются:
 f(х)=
+
f(х)=
+
 f(х)=
+
f(х)=
+
 f(х)=
f(х)=
 f(х)=
f(х)=
Замечание.
Иногда
рассматривают функцию f(х), стремящуюся
к
 при х
при х +
+ ,
при х
,
при х ,
и стремящуюся к +
,
и стремящуюся к + и к
и к
 на бесконечности.
на бесконечности.
Например.
Пусть
f(х) имеет стандартную область определения
Х, Х –неограниченно снизу, тогда
 f(х)=
+
f(х)=
+ определяется так:
определяется так:
 (Г)4
(К)4
(Г)4
(К)4
 {хn}
{хn}
 :
:
 Е>0
Е>0
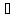 D>0
D>0
 х
(х
х
(х Х,
х<
Х,
х< D):
D):
 f(хn)=
+
f(хn)=
+
 f(х)>Е
f(х)>Е
 Е>0
Е>0

 n>N:
f(хn)>Е
n>N:
f(хn)>Е
§8. Сравнение бесконечно малых и бесконечно больших функций.
-
Определение.
Пусть
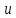 (х)
имеет стандартную область определения
Х и точка хо
лежит внутри или является концом одного
из промежутков, образующих Х.
(х)
имеет стандартную область определения
Х и точка хо
лежит внутри или является концом одного
из промежутков, образующих Х.
Функция
 (х)
называется бесконечно малой при х
(х)
называется бесконечно малой при х хо,
если
хо,
если
 (х)=0.
(х)=0.
Определение.
Пусть
 (х)
и
(х)
и
 (х)
имеют общую стандартную область
определения Х, и обе являются бесконечно
малыми при х
(х)
имеют общую стандартную область
определения Х, и обе являются бесконечно
малыми при х хо.
хо.
Говорят,
что б.м.
 (х)
и
(х)
и
 (х)
при х
(х)
при х хо
имеют один и тот же порядок малости и
пишут
хо
имеют один и тот же порядок малости и
пишут
 (х)=
(х)= x
x xo[
xo[ (х)],
если
(х)],
если
 =L
=L 0.
0.
Замечание.
Мы
в данном случае предполагаем, что
отношение
 определено на Х
определено на Х (хо-h,
хо+h),
h>0, то есть
(хо-h,
хо+h),
h>0, то есть
 (х)
(х) 0
несмотря на то, что
0
несмотря на то, что
 (х)=0.
(х)=0.
Определение.
Говорят,
что две б.м.
 (х)
и
(х)
и
 (х)
при х
(х)
при х хо
эквивалентны,
если
хо
эквивалентны,
если
 =1.
=1.
Определение.
Говорят,
что б.м.
 (х)
при х
(х)
при х хо
имеет более
высокий порядок малости
относительно б.м.
хо
имеет более
высокий порядок малости
относительно б.м.
 (х)
при х
(х)
при х хо,
если
хо,
если
 =0
и пишут
=0
и пишут
 (х)=
(х)= х
х хо[
хо[ (х)].
(х)].
Определение.
Говорят,
что б.м.
 (х)
при х
(х)
при х хо
имеет порядок малости равный р относительно
б.м.
хо
имеет порядок малости равный р относительно
б.м. (х)
при х
(х)
при х хо,
если
хо,
если
 =L
=L 0
и пишут
0
и пишут
 (х)=
(х)= x
x xo[
xo[ р(х)].
р(х)].
Определение.
Если
не существует
 ,
и функция
,
и функция
 при х
при х хо,
то говорят, что б.м.
хо,
то говорят, что б.м.
 (х)
и
(х)
и
 (х)
при х
(х)
при х хо
несоизмеримы.
хо
несоизмеримы.
Примеры.
-
 (х)=х
и
(х)=х
и
 (х)=│x│
при х
(х)=│x│
при х 0
несоизмеримы.
0
несоизмеримы. -
 (х)
и │
(х)
и │ (х)│
- б.м., при х
(х)│
- б.м., при х хо несоизмеримы.
хо несоизмеримы. -
f(х)=х и g(х)=х·
 - б.м. при х
- б.м. при х 0
0
 g(х)=
g(х)= x
x 0[
0[ ]
]
 р=
р= – порядок малости при х
– порядок малости при х 0
относительно х.
0
относительно х.
-
Бесконечно большие –б.б.
Пусть
 (х)
и
(х)
и
 (х)
– бесконечно большие функции при х
(х)
– бесконечно большие функции при х хо.
хо.
Определение.
Говорят,
что б.б.
 (х)
и
(х)
и
 (х)
имеют один и тот
же порядок роста
при х
(х)
имеют один и тот
же порядок роста
при х хо
и пишут
хо
и пишут
 (х)=
(х)= x
x xo[
xo[ (х)],
если
(х)],
если
 =L
=L 0.
0.
Определение.
Говорят,
что б.б.
 (х)
имеет порядок
роста равный р
относительно
(х)
имеет порядок
роста равный р
относительно
 (х)
при х
(х)
при х хо,
если
хо,
если
 =L
=L 0
и пишут
0
и пишут
 (х)=
(х)= x
x xo[
xo[ р(х)].
р(х)].
Определение.
Говорят,
что б.б.
 (х)
более высокого
порядка роста
относительно б.б.
(х)
более высокого
порядка роста
относительно б.б.
 (х)
при х
(х)
при х хо,
если
хо,
если
 =
=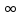 .
.
