Классическая механика Формулировка

В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.

Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть никуда.

Примеры

Классическим примером этого утверждения являются пружинный или математический маятники с пренебрежимо малым затуханием. В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно. В случае математического маятника аналогично ведёт себя потенциальная энергия груза в поле силы тяжести.

Вывод из уравнений Ньютона

Закон сохранения механической энергии может быть выведен из второго закона Ньютона, если учесть, что в консервативной системе все силы, действующие на тело, потенциальны и, следовательно, могут быть представлены в виде

,

где  — потенциальная энергия материальной точки ( — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид

,

где m — масса частицы,  — вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что , можно получить

Путём элементарных операций это выражение может быть приведено к следующему виду

Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной.

Этот вывод может быть легко обобщён на систему материальных точек

9. Угловое ускорение. Момент силы.

Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно:

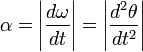
Вектор углового ускорения α направлен вдоль оси вращения (в сторону при ускоренном вращении и противоположно  — при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени, то есть

,

и направлен по касательной к годографу вектора в соответствующей его точке.

Существует связь между тангенциальным и угловым ускорениями:

a_τ = αR,

где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/сек² .

Момент силы— векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

10. Второй закон Ньютона при вращательном движении. Момент инерции.

вращающий момент тела

или

Это выражение представляет собой аналог второго закона Ньютона для вращательного движения, из которого следует, что угловое ускорение твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции Относительно этой оси. Из этого выражения следует, что момент инерции U является мерой его инертности во вращательном движении вокруг неподвижной оси. В случае поступательного движения мерой инертности, как известно, является масса тела.

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

• m_i — масса i-й точки,

• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

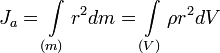где:

• dm = ρdV — масса малого элемента объёма тела dV,

• ρ — плотность,

• r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то