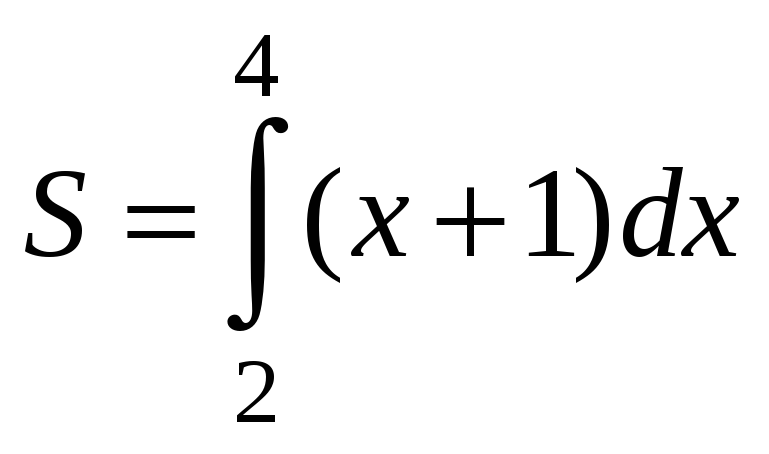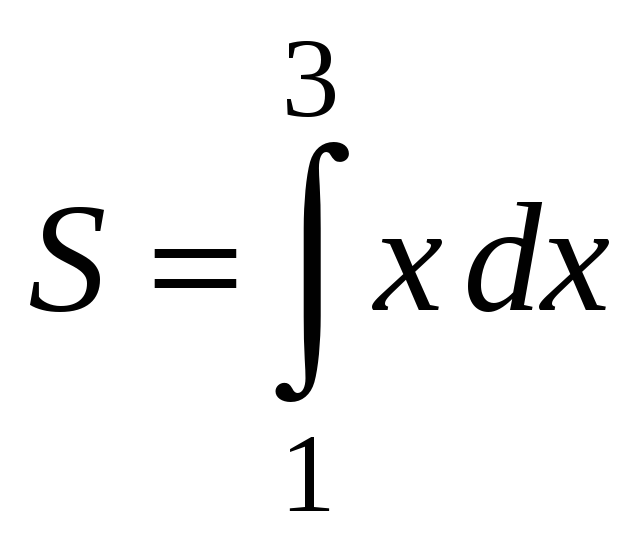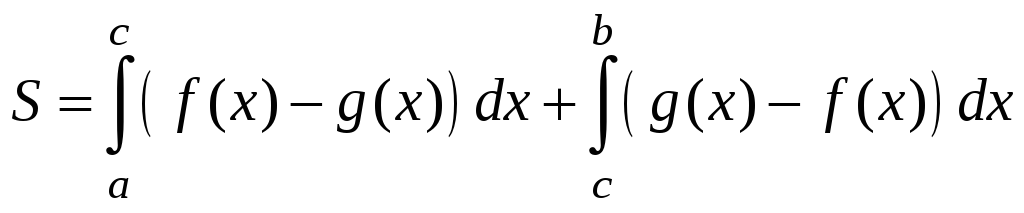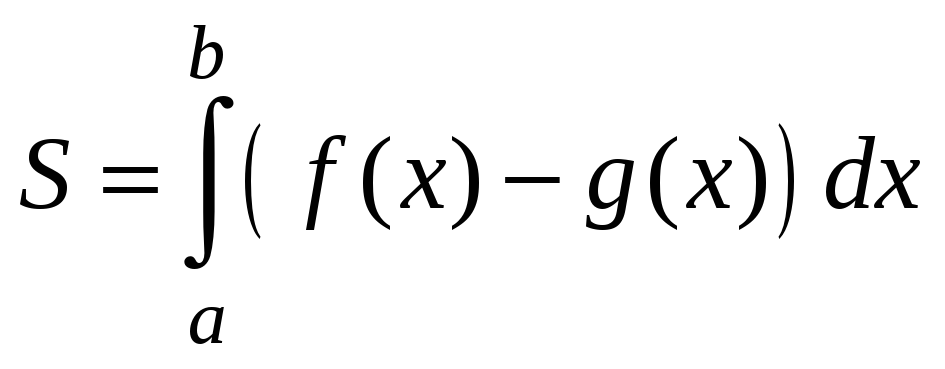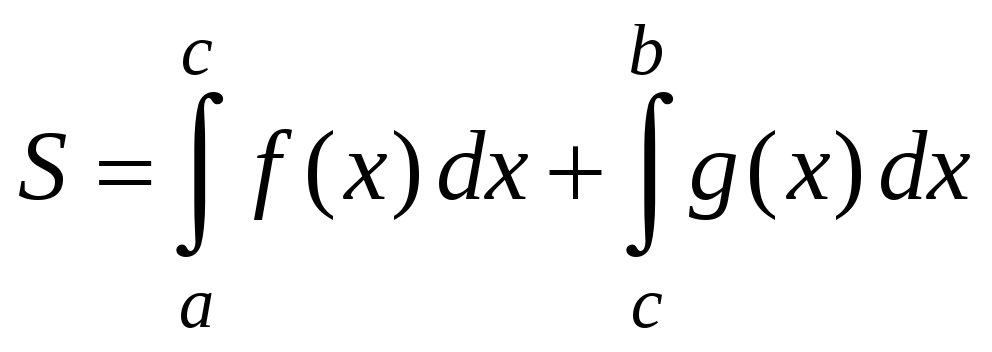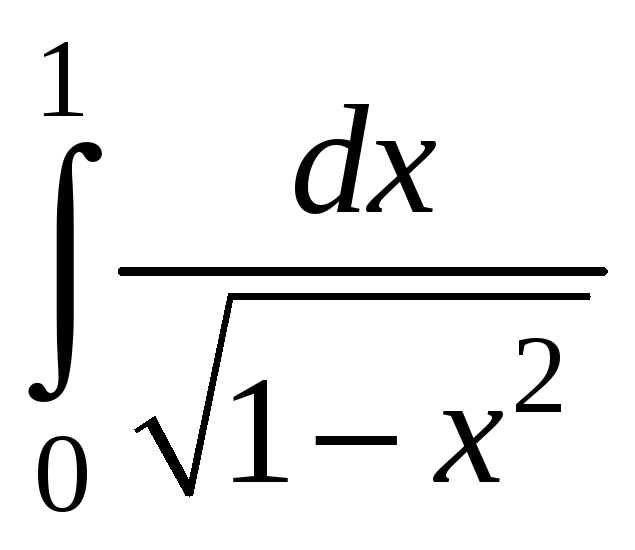- •Учебная дисциплина
- •1. Физическая культура
- •Краткая программа практическИх занятИй
- •ТеоретическИе занятИя
- •I раздел
- •Учебная дисциплина 2. «информатика»
- •Примерная программа лекционного курса
- •Краткая программа практических занятий
- •Литература (основная)
- •Литература (дополнительная)
- •Самостоятельная работа
- •Примерные вопросы к зачету
- •Краткая программа семинарских занятий
- •Литература (основная)
- •Литература (дополнительная)
- •Задания для самостоятельной работы
- •Примерные вопросы к зачету
- •Учебная дисциплина
- •Краткая программа практических занятий
- •Литература (основная)
- •Литература (дополнительная)
- •Интернет-ресурсы
- •Задания для самостоятельной работы
- •Примерные вопросы к зачету
- •Учебная дисциплина
- •Литература (основная)
- •Учебная дисциплина
- •6. Математика
- •Краткая программа лекционого курса
- •Краткая программа семинарских занятИй
- •Приложения математического анализа в дисциплинах по специальности:
- •ЛитературА (основная)
- •ЛитературА (дополнительная)
- •Задания для самостоятельной работы
- •Темы индивидуальных заданий
- •Примерные вопросы к экзамену
- •Учебная дисциплина
- •7. Русский язык и культура речи
- •Краткая программа лекционного курса
- •Краткая программа практических занятий
- •Литература (основная)
- •Литература (дополнительная)
- •Словари и справочники
- •Интернет-ресурсы
- •Задания для самостоятельной работы
- •Тема 1. Язык, речь. Лингвистический и экстролингвистический аспекты понятия «Культура речи», современная теоретическая концепция культуры речи.
- •Тема 2. Речевой этикет.
- •Тема 3. Виды речевой деятельности.
- •Тема 4. Текст, eго признаки, описание, повествование, рассуждение.
- •Тема 5. Стилевые разновидности русского языка.
- •Тема 6. Коммуникативные качества речи. .
- •Тема 7.Точность речи.
- •Тема 8. Основы мастерства публичного выступления.
- •Примерные вопросы к зачету
- •Учебная дисциплина
- •8. Социология
- •Краткая программа лекционного курса
- •Краткая программа семинарских занятий
- •Задания для самостоятельной работы Вопросы для самопроверки и повторения
- •Литература (основная)
- •Литература (дополнительная)
- •Периодическая литература, интернет-ресурсы
- •Примерная тематика докладов и рефератов
- •Примерные вопросы к экзамену
- •Кодекс менеджера-лидера
- •Правила внутреннего распорядка для студентов мгада
- •Студент имеет право:
- •Студент обязан:
- •Ответственность за нарушение дисциплины
- •Отчисление и восстановление
- •Настоящими правилами запрещается:
Приложения математического анализа в дисциплинах по специальности:
-
функции спроса и предложения, бюджетное множество, функция издержек и кривая средних издержек, функция дохода, функции среднего дохода (теория функций);
-
зависимость налоговой ставки от дохода, кривая Торнквиста (пределы последовательностей и функций);
-
предельные издержки, предельная производительность ресурса, предельная норма замены, непрерывное начисление доходов (дифференциальное исчисление);
-
логистическая кривая, максимизация прибыли в модели однопродуктовой формы, коэффициент эластичности, граница множества производственных возможностей (численные методы, приложения производной);
-
изокосты, изокванты производственной функции Кобба–Дугласа, кривые безразличия, коэффициенты эластичности многофакторной функции, предельная производительность труда, модели и методы долгосрочного прогнозирования (функции многих переменных);
-
максимизация прибыли многопродуктовой фирмы, максимизация функции полезности на бюджетном множестве, максимизация прибыли многопродуктовой фирмы на множестве производственных возможностей (экстремумы функций многих переменных);
-
формула вычисления среднегодового значения основных фондов, средняя производительность труда и фондоотдача, вычисление объемов производства, дисконтированный доход (интегральное вычисление);
-
изменение отдачи технологии во времени, кумулятивная (совокупная) отдача, средняя производительность отрасли (несобственные интегралы);
-
статистика с кластерным анализом, необходимым в специальных разделах маркетинга:
-
в логистике,
-
в экологическом менеджменте,
-
в приближенных методах расчета во всех дисциплинах.
-
ЛитературА (основная)
-
Бардушкина И.В., Кожухов И.Б., Ревякин А.М., Терещенко А.М. Математический анализ. Сборник заданий для самостоятельной работы студентов. Учебно-методическое пособие, – МГАДА, 2009. – 59 с.
-
Блинкова Н.А., Ревякин А.М., Терещенко А.М. Дифференциальные уравнения. Серия «Высшая математика для экономистов» Учебное пособие, – МГАДА, 2009. – 86 с.
-
Кремер Н.Ш. и др. Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям.- М.: ЮНИТИ-ДАНА, 2007. – 476 с.
-
Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике: Учебник. В 2-х частях. Ч.2. – М.: Финансы и статистика, 2001. – 376 с.
-
Малыхин В.И. Математика в экономике: Учебное пособие. – М.: ИНФРА-М, 2002. – 352 с.
ЛитературА (дополнительная)
-
Аллавердиев А.М., Блинкова Н.А., Пиндрикова Л.В., Платонова И.В. Математический анализ: Учебно-методическое пособие. М., 2004.
-
Ильин В.А., Садовничий В.А, Сендов Б.Х. Математический анализ. М.: Изд-во МГУ, 1985.
-
Фихтенгольц Г.М. Курс математического анализа. М.: Физматгиз, 1962.
-
Рудин У. Основы математического анализа. М.: Мир, 1976.
-
Кудрявцев Л.Д. Курс математического анализа. М.: Высшая школа, 1981.
-
Никольский С.М. Курс математического анализа. М.: Наука, 1990.
ИНТЕРНЕТ РЕСУРСЫ
Сайт www.rutracker.org/forum/view forum.php содержит PDF-файлы многих учебников и задачников.
ТЕМАТИКА КОНТРОЛЬНЫХ РАБОТ.
Контрольная работа № 1
Базовый уровень.
-
Точка А(-3,3) принадлежит графику функции
 .
Как меняются координаты точки А
при поэтапном преобразовании графика
функции
.
Как меняются координаты точки А
при поэтапном преобразовании графика
функции
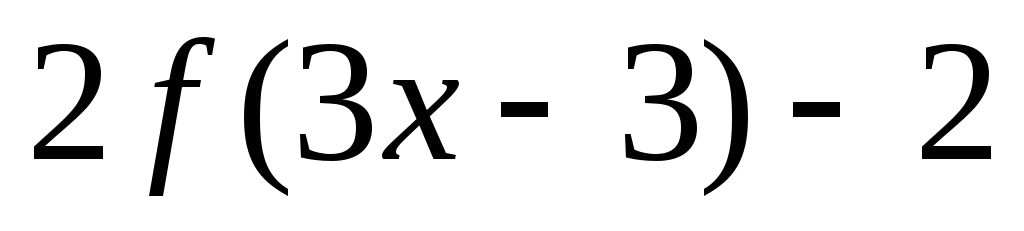 ?
Указать этапы построения.
?
Указать этапы построения. -
Вычислить
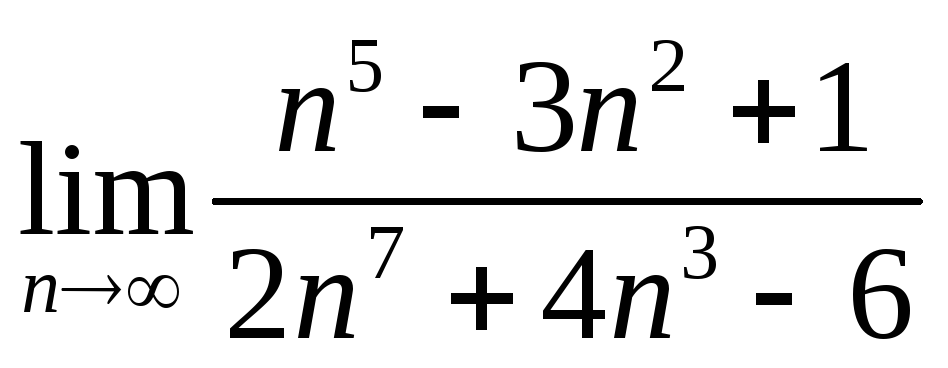 .
. -
Вычислить
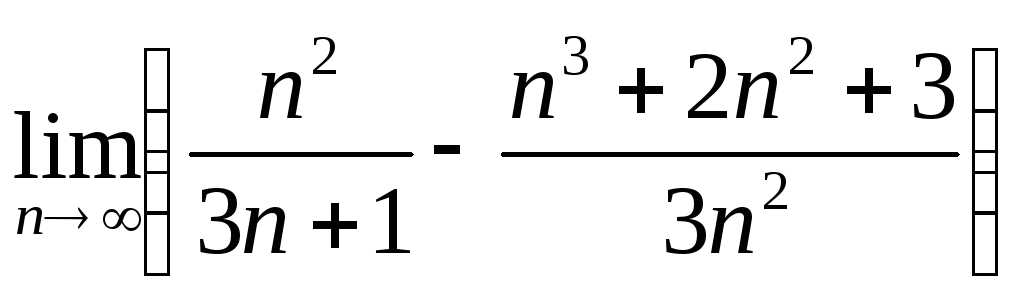 .
. -
Вычислить
 .
. -
Вычислить
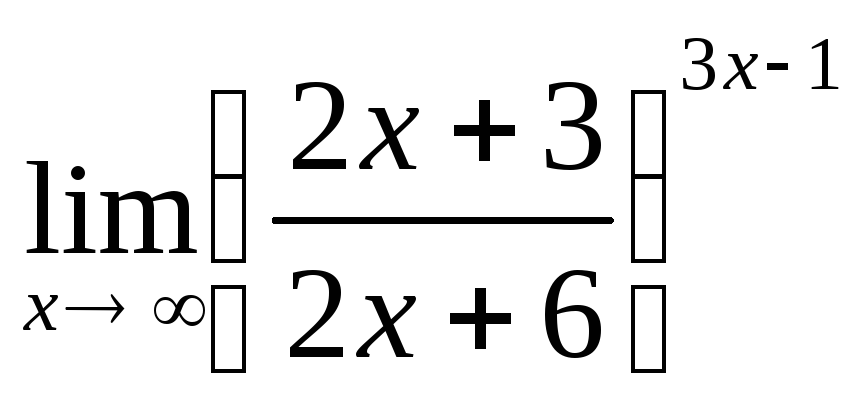 .
.
Повышенный уровень.
-
Вычислить
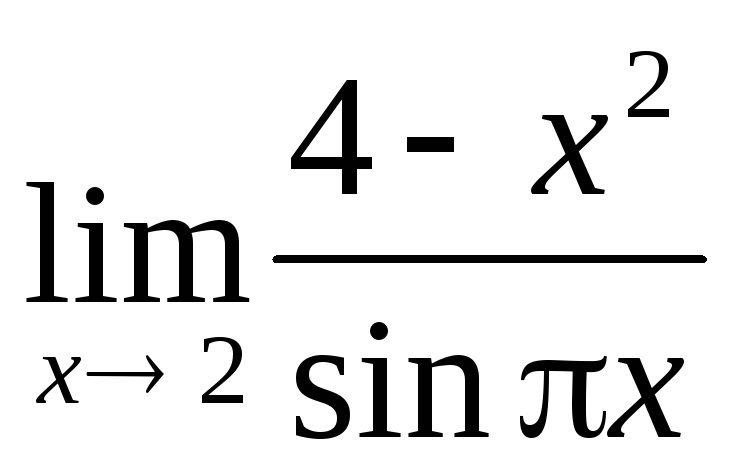 .
. -
При каком а функция f(x) будет непрерывна? Дать геометрическую иллюстрацию.
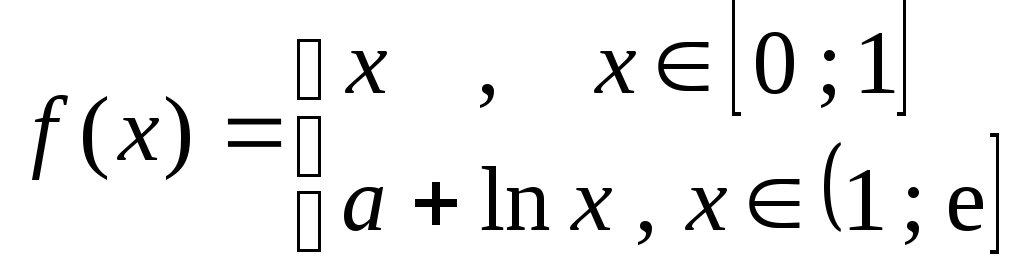
Контрольная работа № 2
Базовый уровень.
Найти производные от функций:
а)
![]() ; б)
; б)![]() ; в)
; в)
![]() .
.
Найти уравнения
касательной и нормали к кривой
![]() в точке
в точке
![]() .
.
Вычислить приближенно
с помощью первого дифференциала
![]() .
.
Найти экстремумы
и промежутки монотонности функции
![]() .
.
Повышенный уровень.
Вычислить предел
с помощью правила Лопиталя ![]() .
.
Компьютерный тест
|
Дидактическая единица |
Формулировка вопроса |
Варианты ответа |
Правиль-ный ответ(ы) |
|
Множества |
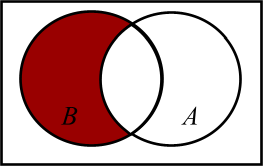
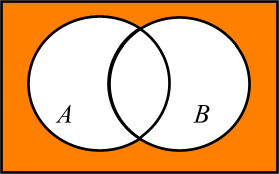
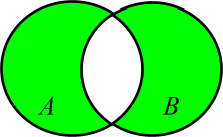
Установить соответствие между выражениями и диаграммами Венна.
1.
2.
3.
|
а)
б)
в)
|
1 – а) 2 – б) 3 – в) |
|
Множества |
Заданы два множества:
|
1)
2)
3)
4) |
1) 2) 3) |
|
Графики элементарных функций. Преобразование графиков |
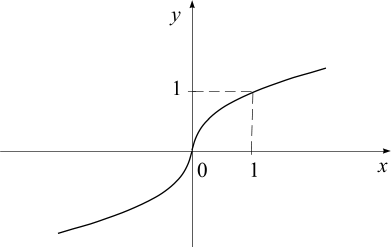
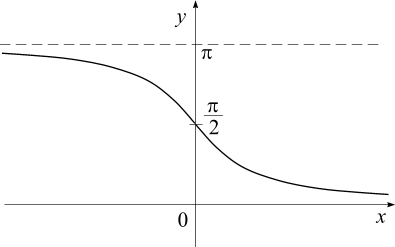
Установить соответствие между функциями и их графиками.
1.
2.
3.
|
а)
б)
в)
г)
|
1 – а) 2 – б) 3 – в) |
|
Графики элементарных функций. Преобразование графиков |
Какое преобразование нужно сделать,
чтобы от графика
|
1)Сдвиг на 1 единицу влево 2) Сдвиг на 1 единицу вправо 3) Сдвиг на 1 единицу вверх 4) Сдвиг на 1 единицу вниз |
1) |
|
Предел последова-тельности |
2-й член последовательности
|
|
|
|
Предел последова-тельности |
Отметьте возрастающие последовательности |
|
1) 2) |
|
Предел последова-тельности |
Установить соответствие между выражениями и значениями пределов:
1.
3.
|
а)
е)
|
1 – а) 2 – б) 3 – в) 4 – г) |
|
Предел последова-тельности |
Предел последовательности
|
|
1
|
|
Предел последова- тельности |
Предел последовательности
равен |
1)
4) 0; 5)
|
1) |
|
Предел последова-тельности |
Отметьте бесконечно малые последовательности |
|
1) 2) |
|
Предел последова-тельности |
Предел последовательности
|
|
1) |
|
Простые и cложные проценты |
Банк выдаёт кредит предприятию в 100 тыс. руб. на 1 месяц по ставке 24% годовых. Проценты начисляются по истечении месяца. Вычислить сумму возврата кредита с учётом процентов. |
|
1) |
|
Простые и сложные проценты |
Вкладчик заключает договор с банком на срок 6 месяцев, процентная ставка – 20% годовых с ежемесячным начислением процентов. Сумма вклада 50 тыс. руб. Через 6 месяцев сумма вклада составит |
|
1) |
|
Предел функции |
Предел функции
равен |
1)
2) 0 3) 10 4) 1 |
1) |
|
Предел функции |
Предел функции
равен |
|
2 |
Контрольная работа № 3
Базовый уровень.
1. Вычислить неопределённые интегралы:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() .
.
2.
Вычислить определённые интегралы: 1)
![]() ; 2)
; 2)
 .
.
3.
Найти площадь фигуры, заключенной между
кривыми
![]() ,
,
![]() .
.
Повышенный уровень.
4.
Вычислить несобственный интеграл или
установить расходимость
![]()
Контрольная работа № 4
Базовый уровень.
1. Найти область
определения функции
![]() .
Изобразить на плоскости.
.
Изобразить на плоскости.
2.
Найти
![]() функции
функции
![]() ,
где
,
где
![]() ,
,
![]() .
.
3.
Найти экстремумы функции
![]() .
.
Повышенный уровень.
4.
Вычислить приближенно
![]() .
.
Найти производную
функции
![]() в начале координат в направлении вектора
в начале координат в направлении вектора
![]() .
.
Контрольная работа № 5
Базовый уровень.
-
Исследовать на сходимость ряд
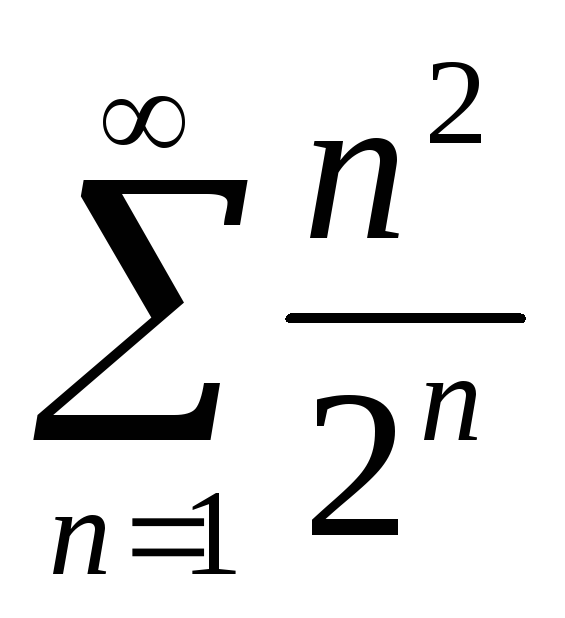 .
. -
Исследовать на сходимость ряд
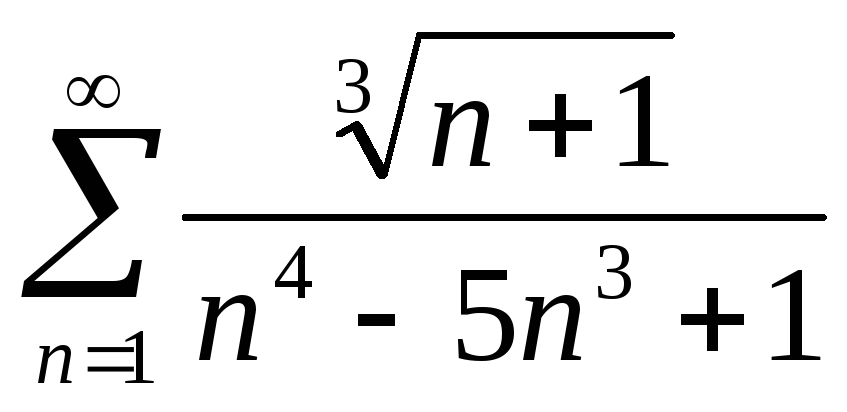 .
.
3. Вычислить двойной
интеграл
![]() ,
где D
– область,
ограниченная кривыми
,
где D
– область,
ограниченная кривыми
![]() ,
,
![]() ,
,
![]() .
.
Повышенный уровень.
-
Исследовать на абсолютную и условную сходимость ряд
 .
.
-
Исследовать на абсолютную, условную и равномерную сходимость степенной ряд
![]() .
.
Компьютерный тест
|
Дидакти-ческая единица |
Формулировка вопроса |
Варианты ответа |
Прави льный ответ |
|
Определён-ный интеграл |
Отметьте верные равенства |
1)
2)
3)
4)
|
1) 2) |
|
Определён-ный интеграл |
Интеграл
|
|
2 |
|
Определён-ный интеграл |
Интеграл
|
1)
4)
|
1) |
|
Определён-ный интеграл |
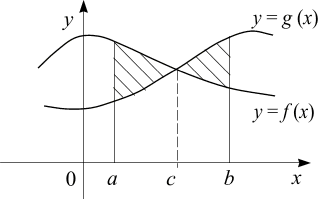
Площадь фигуры, изображённой на рисунке, вычисляется:
|
1)
2)
3)
4)
|
1) |
|
Определён-ный интеграл |
Отметьте верную формулу для вычисления площади фигуры
|
1)
2)
3)
4)
|
1) |
|
Определён-ный интеграл |
Отметьте сходящиеся интегралы |
1)
4)
|
1) 2) |
|
Определён-ный интеграл |
Определить значение несобственного
интеграла
|
1)
5) интеграл расходящийся |
1) |
|
Функции многих перемен-ных |
Отметьте функции, определённые на всей плоскости Oxy |
1)
2)
4)
|
1) 2) |
|
Функции многих перемен-ных |
Значение функции
точке
|
|
1 |
|
Функции многих перемен-ных |
Если
то значение
|
|
2 |
|
Функции многих перемен-ных |
Отметьте частные производные
1-го порядка для
функции
|
1)
3)
5)
7)
|
1) 2) |
|
Функции многих перемен-ных |
Отметьте правильные
выражения для указанных частных
производных функции
1)
|
а)
г)
|
|
|
Функции многих перемен-ных |
Значение смешанной производной
равно |
|
0 |
|
Функции многих перемен-ных |
Частная производная
|
1)
4)
|
1) |
|
Функции многих перемен-ных |
Отметьте выражение для
дифференциала
1-го порядка функции
|
1)
2)
3)
4)
|
1) |


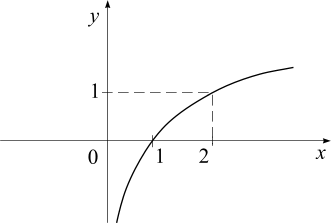
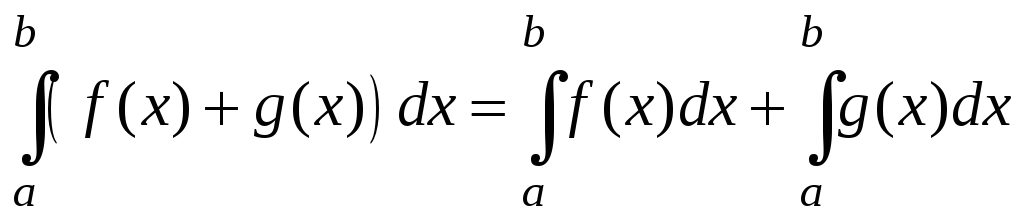
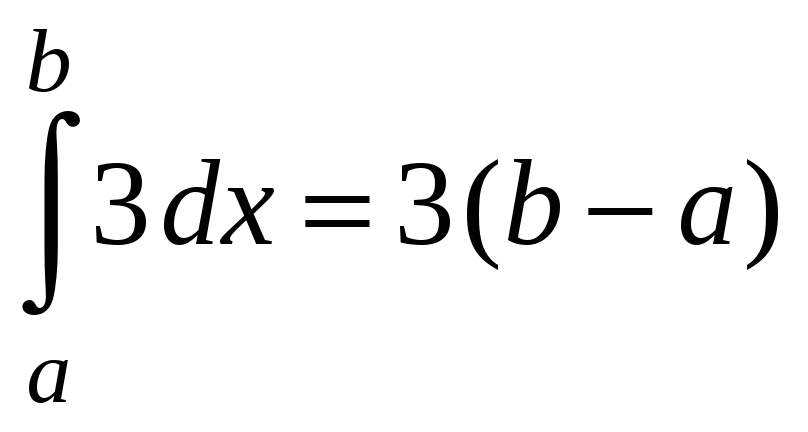

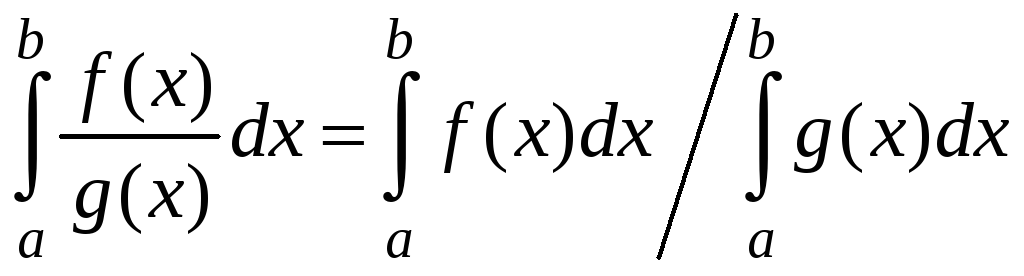
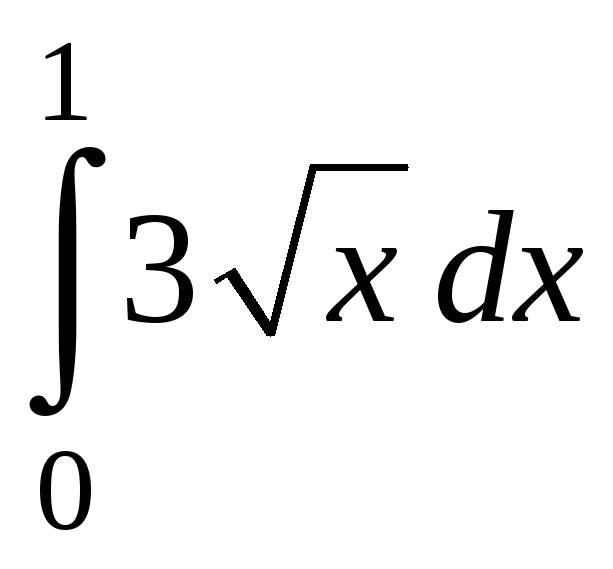 равен
равен