Методы оценки колеблемости ряда и типичности средних величин

Средние арифметические величины, взятые сами по себе без учета колеблемости рядов, из которых они вычислены, имеют подчас ограниченное значение. Средние — это величины, вокруг которых рассеяны различные варианты, поэтому понятно, что чем ближе друг к другу отдельные варианты по своей количественной характеристике, тем меньше рассеяние, колеблемость ряда, тем типичнее его средняя. Одинаковые по размеру средние могут быть получены из рядов с различной степенью рассеяния.

Приблизительно о колеблемости можно судить по амплитуде (размаху) вариационного ряда — разности максимальной и минималь­ной вариант. Символика обозначения амплитуды: Am = Vmax-Vmin.

Основной, общепринятой мерой колеблемости вариационного ряда является среднее квадратическое отклонение, обозначаемое греческой буквой а (сигма малая).

Чем больше среднее квадратическое отклонение, тем, следовательно, степень колеблемости данного ряда выше. Так, при определении средней длительности послеоперационного лечения аппендицита в двух больницах были получены следующие результаты:

Больница 1	Больница 2
М=9 дней	М=9 дней
Σ=±2 дня	Σ=±4 дня

Средняя длительность лечения в обеих больницах одинакова. Однако в первой больнице сроки послеоперационного лечения у отдельных больных были близки к 9 дням. Во второй больнице колебания были значительнее, отсюда и среднеквадратическое отклонение здесь больше, и следовательно, полученная средняя величина послеоперационного периода является менее типичной, чем в первой больнице.

Среднее квадратическое отклонение характеризует среднее отклонение всех вариант вариационного ряда от средней арифметической величины. Поскольку отклонения вариант от средней, как было сказано выше, имеют значения с «+» и «-», то при суммировании они взаимоуничтожаются. Чтобы избежать этого, отклонения возводятся во вторую степень, а затем, после определенных вычислений, производится обратное действие — извлечение корня квадратного. Поэтому среднее отклонение именуется квадратическим.

Среднее квадратическое отклонение определяют по формуле:

Ход вычислений при определении среднеквадратического отклонения следующий:

1. возвести каждое отклонение d во вторую степень;

2. умножить квадрат каждого отклонения d² на соответствующую частоту р;

3. суммировать полученные произведения Sd²p ;

4. разделить данную сумму на количество вариант, входящих в вариационный ряд л (при числе наблюдений менее 30 сумма делится на n-1);

5. извлечь квадратный корень из полученного частного.

Расчеты представлены в табл. 2 (I способ). Подставив полученные значения в формулу, находим среднеквадратическое отклонение:

При вычислении среднеквадратического отклонения по способу моментов используется следующая формула:

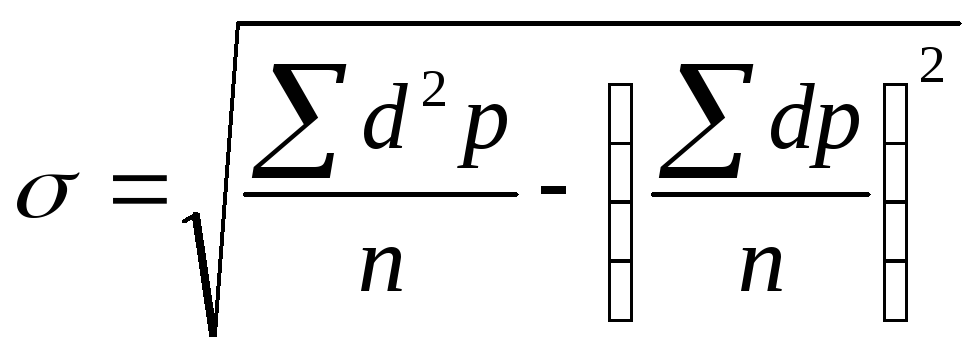
В чем суть этой формулы? Как видно, первая часть данного подкоренного выражения полностью идентична вышеприведенной формуле вычисления среднеквадратического отклонения обычным способом . Однако необходимо указать, что отклонения, находимые для условной средней А, заведомо будут ошибочными, т. е. отличными от отклонений, которые определяются для фактической средней М. Учитывая это обстоятельство, в формулу вносится поправ­ка, которая определяется для условной средней А. Эта поправка назы­вается моментом первой степени . Для разбираемого нами случая она равна + 1,3 (см. с. 11). Поскольку поправка вносится в подкоренное выражение, то она возводится во вторую степень.

Первая часть формулы называется моментом второй степени, т. к. отклонение d возведено во вторую степень.

Таким образом, формула вычисления среднеквадратического отклонения по способу моментов будет читаться как корень квадратный из разности момента второй степени и квадрата момента первой степени.

Определим среднеквадратическое отклонение по способу моментов для рассматриваемого нами примера (табл. 2). Подставив значения в формулу, находим:

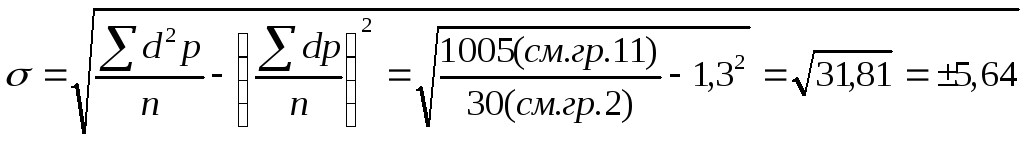
Результаты вычисления среднеквадратического отклонения обычным способом и способом моментов идентичны. Однако, как указывалось выше, второй способ значительно убыстряет и упрощает расчеты.

Итак, нахождение среднеквадратического отклонения позволяет судить о характере однородности исследуемой группы наблюдений. Если величина среднеквадратического отклонения небольшая, то это свидетельствует о достаточно высокой однородности изучаемого явления. Среднюю арифметическую в таком случае следует признать вполне характерной для данного вариационного ряда. Однако слишком малая величина сигмы заставляет думать об искусственном подборе наблюдений. При очень большой сигме средняя арифметическая в меньшей степени характеризует вариационный ряд, что говорит о значительной вариабельности изучаемого признака или явления или о неоднородности исследуемой группы.

Оценка степени рассеяния вариант около средней может быть произведена с помощью коэффициента вариации, вычисляемого по формуле:

Значения коэффициента вариации С менее 10% свидетельствует о малом рассеянии, от 10 до 20% — о среднем, более 20% — о сильном рассеянии вариант вокруг средней арифметической.

Возвращаясь к нашему примеру (табл. 1 и 2), дадим характеристику изучаемому вариационному ряду.

Амплитуда этого вариационного ряда равна 22 годам (61-39 = 22), σ=±5,64, .

Расчеты свидетельствуют о среднем рассеянии вариант, следовательно, средняя арифметическая величина вполне типична, а исследуемая группа наблюдений является достаточно однородной.

Коэффициент вариации часто используется при оценке колеблемости рядов различных признаков, например, веса и роста. Непосредственное сравнение сигм в данном случае невозможно, т. к. среднеквадратическое отклонение — величина, именованная и выраженная абсолютным числом. Предположим, что при изучении физического развития группы подростков коэффициент изменчивости для веса составил 9,7%, а для роста — 4,6%. Эти цифры можно сравнить и сделать заключение, что в данном примере рост является более устойчивым признаком, чем вес.

Определение среднеквадратического отклонения представляет немалую ценность для медицинской науки и практики. При диагностике отдельных заболеваний очень важно оценить на основании конкретных исследований, какие признаки проявляются у соответствующей группы больных относительно одинаково, с небольшими колебаниями, а для каких признаков характерны большие индивидуальные колебания. Очень широко используется это свойство при оценке физического развития отдельных групп населения, при выработке стандартов школьной мебели и т. д.

Согласно теории вероятности в явлениях, подчиняющихся нормальному закону распределения, между значениями средней арифметической, среднеквадратического отклонения и вариантами существует строгая зависимость (правило трех сигм). Например, 68,3% значений варьирующего признака находятся в пределах М ± 1σ , 95,5% — в пределах М ± 2σ и 99,7% — в пределах М ± Зσ .

Данные, полученные эмпирически, не всегда строго совпадают с теоретическими, но они тем ближе к ним, чем больше число наблюдений и однороднее их состав.

Более подробно о применении правила трех сигм можно познакомиться в руководствах или пособиях по медицинской статистике.