1. Скалярное произведение векторов.

   1. Свойства.

   2. Применение.

   3. Выражение через координаты сомножителей.

Проекция вектора на вектор:

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

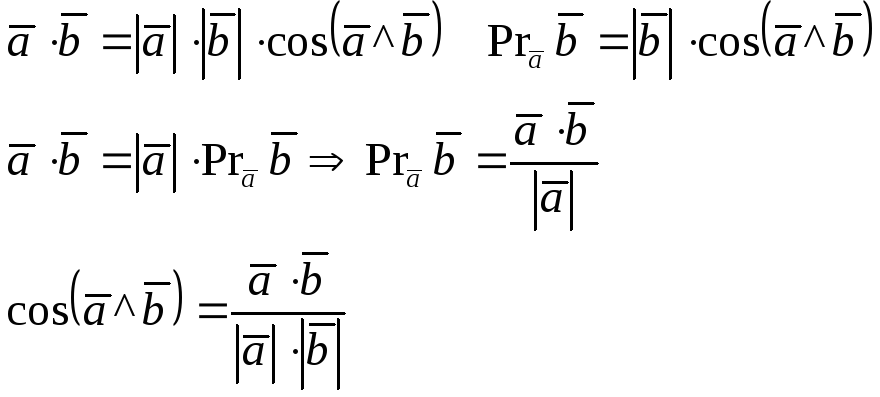
Свойства:

1. – Коммутативность.

2. 

3. 

4. 

5. 

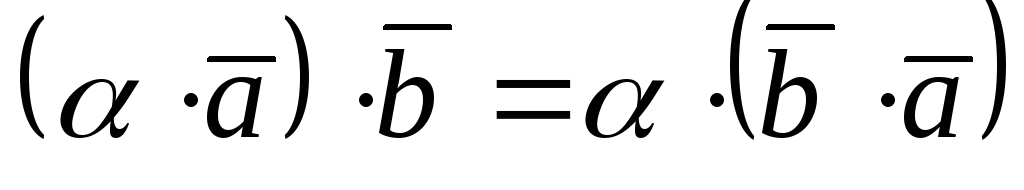
Скалярное произведение векторов, заданных своими декартовыми координатами равно сумме по парных произведений соответствующих координат сомножителей.

Применение скалярного произведения:

1. 

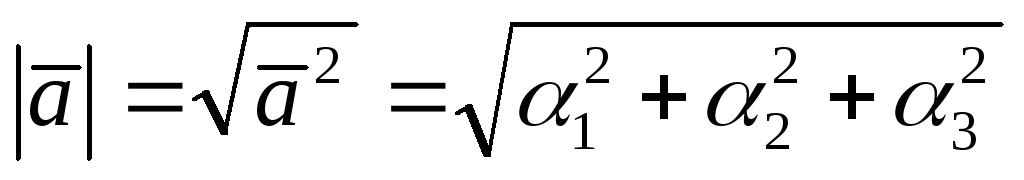
2. Определение перпендикулярности векторов, как скалярное произведение, равное нулю.

3. 

4. 

Вопрос № 19: Векторное произведение векторов:

1. Векторное произведение векторов.

   1. Свойства.

   2. Геометрический смысл.

   3. Выражение через координаты сомножителей.

Векторным произведением векторов называется вектор, обозначаемый , который обладает двумя свойствами:

1. Перпендикулярен двум исходным векторам.

2. Составляет с исходными векторами правую тройку⁵

3. 

Направление результирующего вектора определяется по правилу буравчика.

Свойства векторного произведения:

1. – проверка на колиниарности.

2. 

3. 

4. 

5. 

6. 

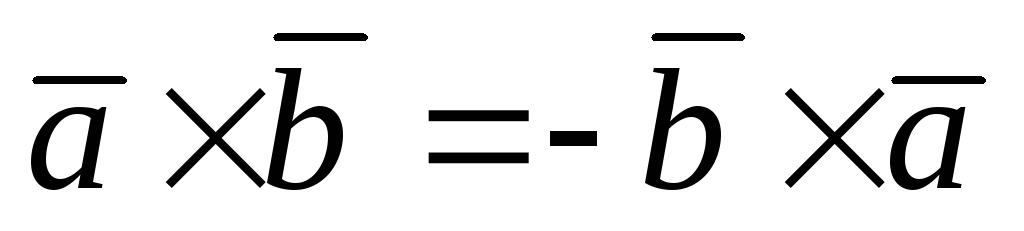
Вопрос № 20: Смешанное произведение векторов:

1. Смешанное произведение векторов.

   1. Свойства.

   2. Геометрический смысл.

   3. Выражение через координаты сомножителей.

Смешанным произведением трёх векторов называется число, обозначаемое , равное скалярному произведению трёх его сомножителей, на векторное произведение двух первых.

1. 0, когда , а значит угол v – острый, следовательно, вектора составляют правую тройку.

2. 0, когда , а значит угол v – тупой, следовательно, вектора составляют левую тройку.

3. 

Свойства смешанного произведения:

1. =0 тогда, когда комплонарны.

2. 

3. 

Вопрос № 21: Прямая на плоскости:

1. Прямая на плоскости.

   1. Уравнения.

      1. Общее.

      2. Параметрическое.

      3. Каноническое.

   2. Расстояние до точки.

   3. Угол между прямыми.

На плоскости задана прямоугольная декартова система координат.

Уравнение называется уравнением линии L на плоскости, если координаты всех точек линии подчиняются закону F, а координаты всех точек, не лежащих на линии .

Линия – это геометрическое место точек, координаты которых удовлетворяют закону – основное уравнение прямой на плоскости.

Векторное уравнение прямой на плоскости:

Параметрическое уравнение прямой на плоскости:

Каноническое уравнение прямой на плоскости:

Расстояние от точки до прямой:

Угол между прямыми:

Вопрос № 22: Плоскость в пространстве:

1. Плоскость в пространстве.

   1. Уравнение:

      1. Общее.

      2. Параметрическое.

      3. Каноническое.

   2. Расстояние до точки.

   3. Угол между плоскостями.

Общее уравнение плоскости в пространстве:

Параметрическое уравнение прямой:

Векторное уравнение плоскости в пространстве:

Расстояние от точки до плоскости:

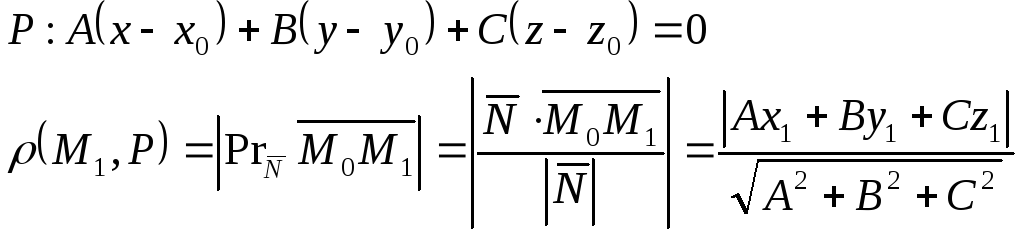
Уравнение плоскости, проходящей через три заданные точки:

Угол между прямой и плоскостью:

Углом между прямой и плоскостью называется любой смежный угол, образованный самой прямой и проекцией этой прямой на плоскости:

Вопрос № 23: Прямая в пространстве:

1. Прямая в пространстве.

   1. Уравнение.

      1. Общее.

      2. Параметрическое.

      3. Каноническое.

      4. Переходы между ними.

   2. Угол между прямыми.

   3. Угол между прямой и плоскостью.

Общее уравнение прямой в пространстве:

Общее уравнение прямой в пространстве выводится из условия задания прямой, как пересечения двух плоскостей:

Параметрическое уравнение прямой:

Каноническое уравнение прямой:

Угол между прямыми:

Угол между прямой и плоскостью:

Вопрос № 24: Три типа взаимного расположения прямых в пространстве:

1. Три типа расположения двух прямых в пространстве:

   1. Параллельные прямые.

   2. Пересекающиеся.

   3. Скрещивающиеся прямые.

2. Расстояния:

   1. Между точкой и прямой.

   2. Между параллельными прямыми в пространстве.

   3. Между скрещивающимися прямыми в пространстве.

Параллельные прямые в пространстве:

Пересекающиеся прямые в пространстве:

Скрещивающиеся прямые:

Вопрос № 25: Кривые второго порядка:

1. Кривые второго порядка.

   1. Типы.

      1. Геометрические определения

      2. Канонические уравнения.

2. Общее уравнение.

   1. Преобразование к каноническому.

      1. Перенос начала координат.

      2. Поворот осей.

Кривой второго порядка называется алгебраическая линия второй степени, общее уравнение которой имеет следующий вид: . Любые уравнения такого вида можно привести к каноническому виду.

Кривые второго порядка подразделяются на Эллипс, Гиперболу и Параболу.

Эллипс:

Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых до двух заданных фокусов есть величина постоянная

Эксцентриситет:

Эксцентриситет характеризует степень сжатия

Коэффициент сжатия:

Параметрическое уравнение эллипса:

Оптические свойства:

Если взять эллиптическое зеркало, и в один из фокусов поместить источник света, то отражённые лучи пересекутся в другом фокусе.

Гипербола:

Гиперболой называется геометрическое место точек плоскости, абсолютная величина разности расстояний каждой из которых до двух заданных фокусов, находящихся на расстоянии 2с является величиной постоянной, равной 2а.

Эксцентриситет:

Оптические свойства:

Гиперболическое зеркало даёт расходящийся пучок света.

Парабола:

П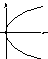араболой называется геометрическое место точек плоскости, каждая из которых равноудалена от заданной точки – фокуса, и заданной прямой, называемой директрисой, причём расстояние от точки до прямой равно р:

Приведение кривой к каноническому виду:

Приведение общего уравнения второго порядка к каноническому виду производится в два действия:

1. Определение новой системы координат, оси которой повёрнуты относительно основной. Поворот определяется слагаемыми, представляющими собой произведение переменных.

2. Сдвиг начала координат вдоль осей новой системы. Сдвиг определяется линейными членами уравнения. Преобразование на данной стадии осуществляется выделением полных квадратов.

– квадратичная форма.

Приведение квадратичной формы к взвешенной сумме квадратов: !!!¿¿¿