
- •Содежание
- •Тема: Совместные исследования уравнения двух прямых
- •Тема: Не полное уравнение прямой
- •Тема: аналитическая геометрия в пространстве
- •Тема: Неполные уравнения плоскости
- •Тема: уравнение плоскости проходящей через три точки
- •Тема: Прямая в пространстве. Канонические и параметрические уравнения прямой.
- •Тема: уравнение прямой, проходящее через 2 точки
- •Тема: Прямая, как пересечение двух плоскостей
- •Тема: Параллельность и перпендикулярность двух плоскостей, двух прямых, прямой и плоскости.
- •Тема: Кривые второго порядка. Эллипс. Вывод канонического уравнения эллипса.
- •Тема: Исследование формы эллипса и его построения.
- •Тема: Эксцентриситет эллипса
- •Тема: Гипербола
- •Тема: Исследование уравнения гиперболы
- •Тема: Эксцентриситет гиперболы
- •Тема: Исследование формы параболы.
- •Тема: Матрица. Понятие матрицы. Основные определения.
- •Тема: Действие над матрицами
- •Тема: свойства умножения матриц
- •Тема: Обратная матрица и ее вычисление
- •Тема: Вычисление обратной матрицы
- •Тема: Решение систем линейных уравнений матричным способом
- •Тема: Дифференциальное исчисление
- •Тема: Неявные и обратные функции.
- •Тема: Понятие числовой последовательности и Эпсилон окрестности точки.
- •Тема: Понятие Эпсилон окружности точки.
- •Тема: Предел последовательности (числовой)
- •Тема: Предел функции
- •Односторонние пределы
- •Предел функции при бесконечном стремлении аргумента.
- •Тема: Не ограниченные и ограниченные функции
- •Тема: бесконечно малые величины и их свойства
- •Тема: Основные теоремы о пределах
- •Тема: Первый замечательный предел
- •Тема: второй замечательный предел. Число e, натуральные логарифмы
- •Тема: Сравнение бесконечно малых величин
- •Тема: Некоторые свойства непрерывной функции.
- •Тема: Условие непрерывности функции
- •Тема: Классификация точек разрыва
- •Тема: Производная и дифференциал
- •Тема: Определение производной ее геометрический и механический смысл.
- •Тема: Механический и геометрический смысл производной.
- •Тема: Дифференцируемость функции
- •Тема: Производные некоторых элементарных функций.
- •Тема: Понятие сложной функции и ее производная
- •Тема: Производная функций и
- •Тема: Производная неявно заданной функции
Тема: бесконечно малые величины и их свойства
Пусть функция
![]() ,
при
,
при
![]() ,
тогда эта функция называется бесконечно
малой величиной при
,
тогда эта функция называется бесконечно
малой величиной при
![]() .
.
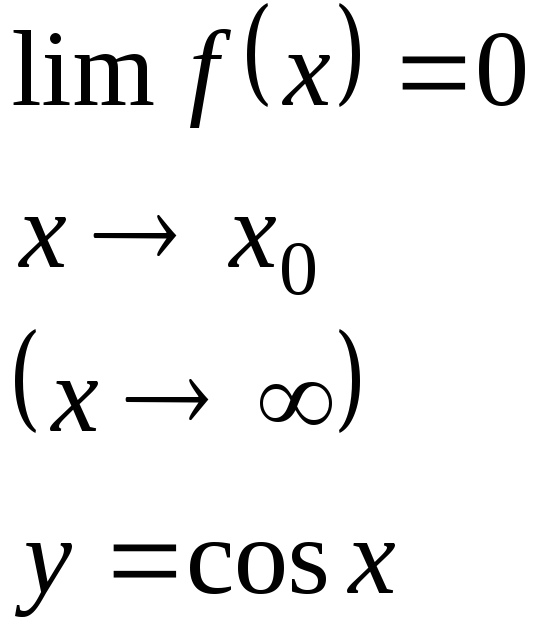
Если
![]()
![]() ,
то функцию можно назвать бесконечно
малой величиной, но если
,
то функцию можно назвать бесконечно
малой величиной, но если
![]() ,
то функцию нельзя назвать бесконечно
малой величиной.
,
то функцию нельзя назвать бесконечно
малой величиной.
Основные свойства
-
Пусть предел функции
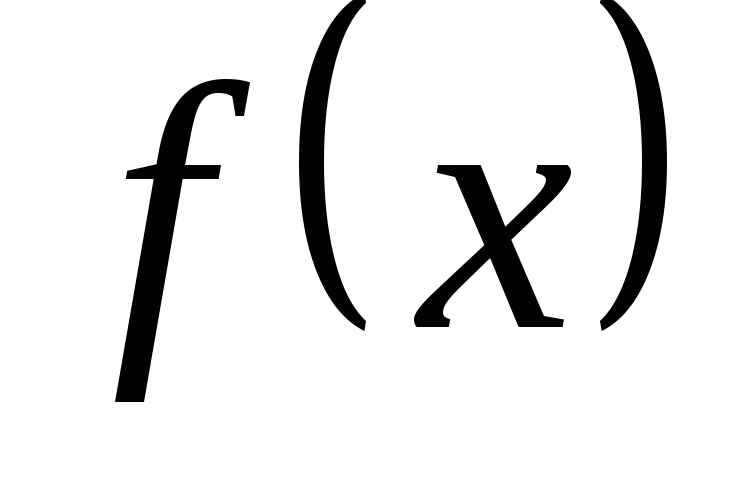 ,
при
,
при
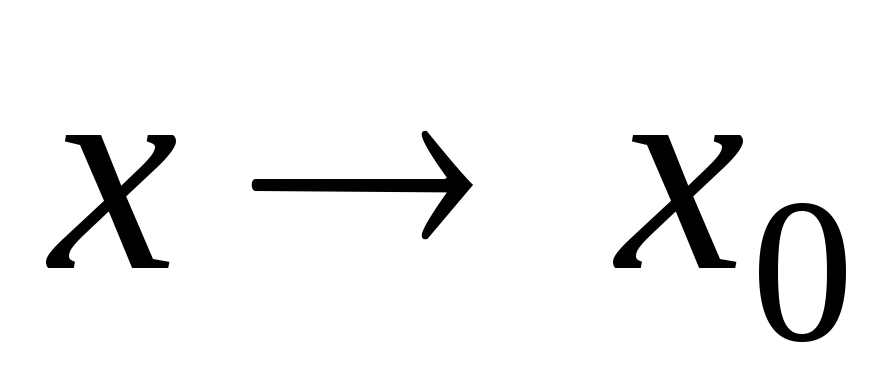
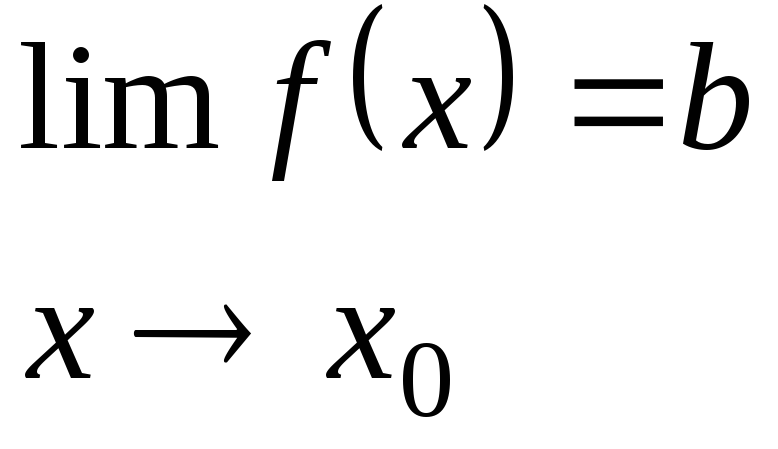 ,
тогда в некоторой окрестности точки
,
тогда в некоторой окрестности точки
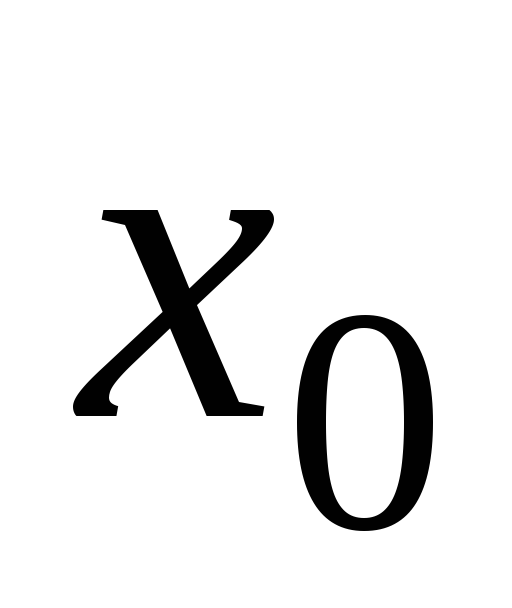 ,
справедливо равенство
,
справедливо равенство
 ,
где
,
где
 бесконечное,
при
бесконечное,
при
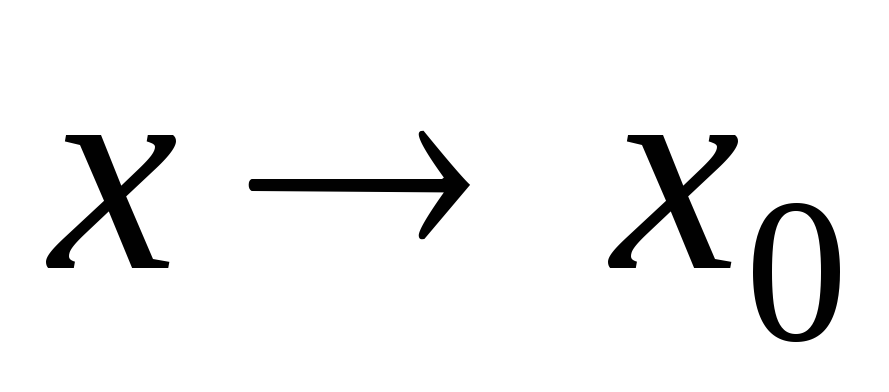 .
.
-
Пусть в некоторой окрестности точки
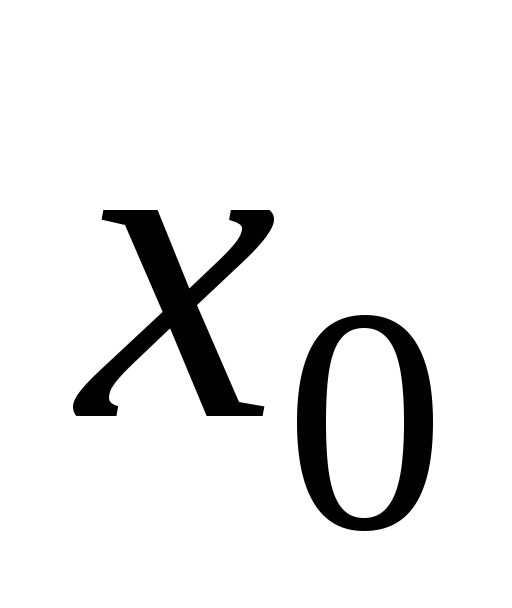 справедливо равенство
справедливо равенство

При
![]() ,
тогда предел этой функции при
,
тогда предел этой функции при
![]() = b
= b
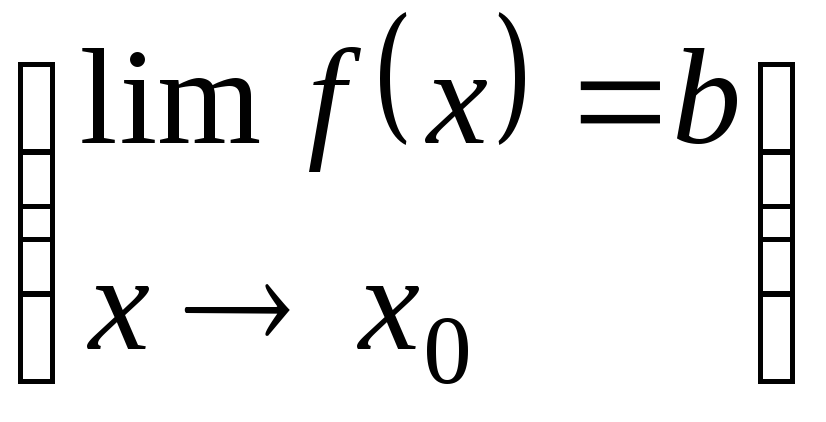
-
если
 ,
при
,
при
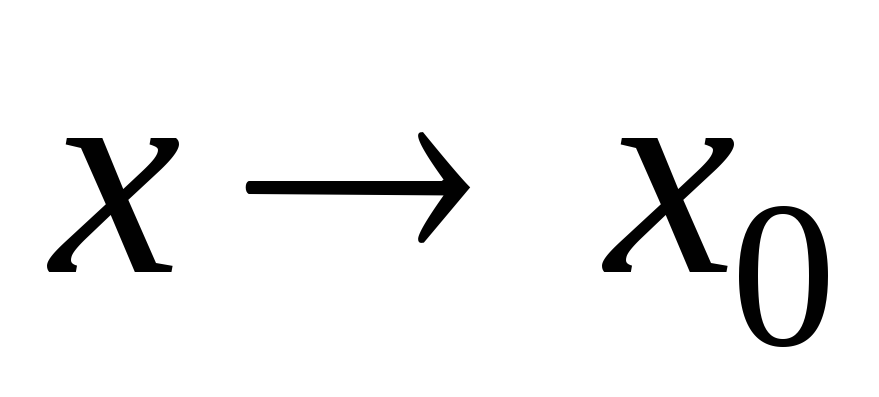 ,
то
,
то
 ,
стремится к бесконечности
,
стремится к бесконечности -
Алгебраическая сума конечного числа точки
 M
величин есть также
M
величин есть также
 Mb
Mb
-
Произведение
 Mb
на ограниченную функцию, есть
Mb
на ограниченную функцию, есть
 Mb
Mb
Следствие
-
Произведение
 M
на постоянную величину есть
M
на постоянную величину есть
 M
M -
Произведение конечного числа
 Mb
есть
Mb
есть Mb
Mb
Тема: Основные теоремы о пределах
Теорема 1
Предел суммы или разности конечного числа слагаемых функций равен соответственно сумме или разности пределов каждой функции
Теорема 2
Предел произведения конечного числа функции равен произведению пределов сомножителей
Теорема 3
Предел частного двух функций равен отношению их пределов, если предел знаменателя отличен от 0
Теорема 4
Пусть функция
![]() удовлетворяет условию:
удовлетворяет условию:
![]() и пусть пределы крайних функций равны
друг другу и равны b, тогда
предел средней функции существует и
равен b
и пусть пределы крайних функций равны
друг другу и равны b, тогда
предел средней функции существует и
равен b
![]()
![]()
lim![]() =
=
![]()
![]()
n! =1·2·3·4…………n
n- Факториал
0!=1, 2!=2
1!=1, 3!=1·2·3=6, 4!=24
Теорема 5
Пусть некоторая
функция y=![]() при
при
![]() стремится
к пределу
стремится
к пределу
![]() ,
принимая при этом все время не отрицательные
значения, тогда предел
,
принимая при этом все время не отрицательные
значения, тогда предел
![]() ,
тогда b также не отрицателен
,
тогда b также не отрицателен
![]()
Теорема 6
Пусть при
![]() две функции
две функции
![]() связанные неравенством стремятся к
некоторым пределам, тогда
связанные неравенством стремятся к
некоторым пределам, тогда
![]() ,
их пределы связаны таким же неравенством
,
их пределы связаны таким же неравенством
Теорема 7
Если переменная величина монотонно возрастает и ограничено сверху числом М, то она имеет предел не превосходящий М.
Тема: Первый замечательный предел
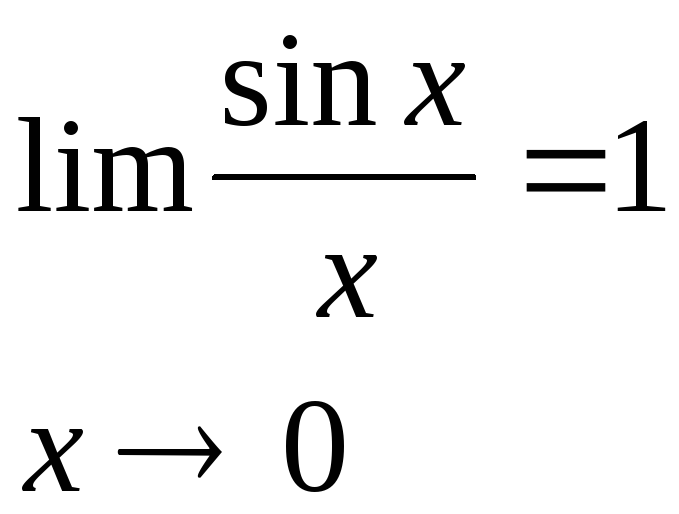
Рассмотрим
S![]()
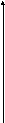

 y D
y D


 A
A
 0 xc B
x
0 xc B
x

Рассмотрим
![]()
![]()
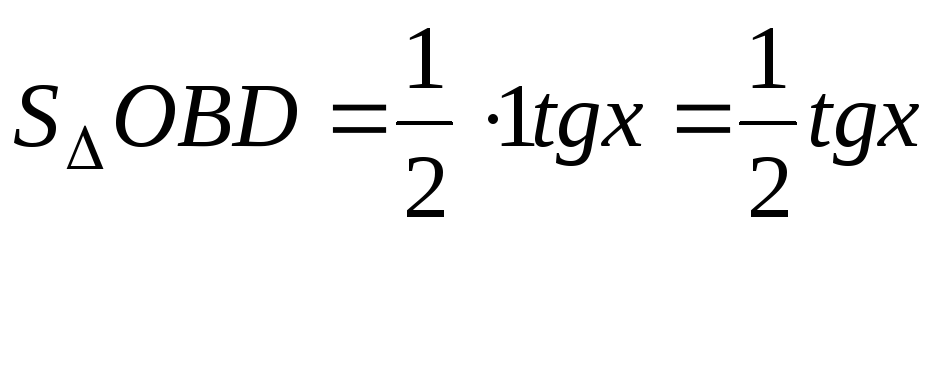

Тема: второй замечательный предел. Число e, натуральные логарифмы
Рассмотрим числовую последовательность
![]()
Теорема:
Предел
последовательности
![]() при
при
![]() равен числу e
равен числу e
![]() иррациональное число
иррациональное число
Теорема:
Рассмотрим
функцию
![]() ,
пусть
,
пусть
![]() принимая при этом иррациональные и
рациональные значения, т.е. непрерывно
принимая при этом иррациональные и
рациональные значения, т.е. непрерывно
![]() ,
тогда можно доказать теорему
,
тогда можно доказать теорему
![]()
Натуральный
логарифм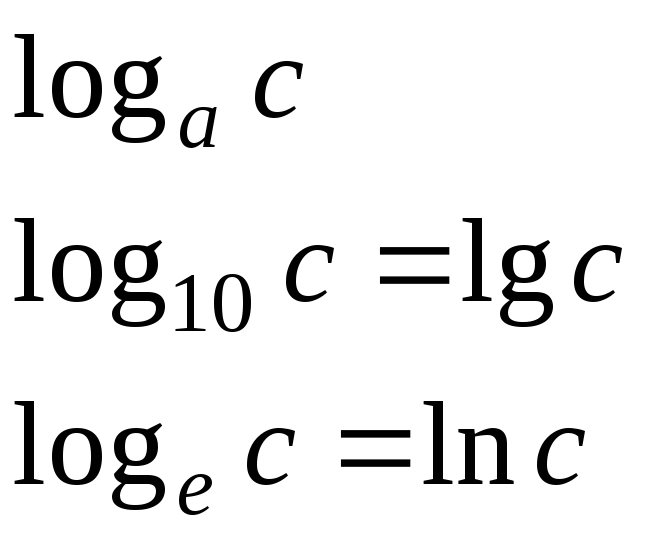
![]() экспонент
экспонент
Найти предел функции:

1 в любой конечной степени остается единицей
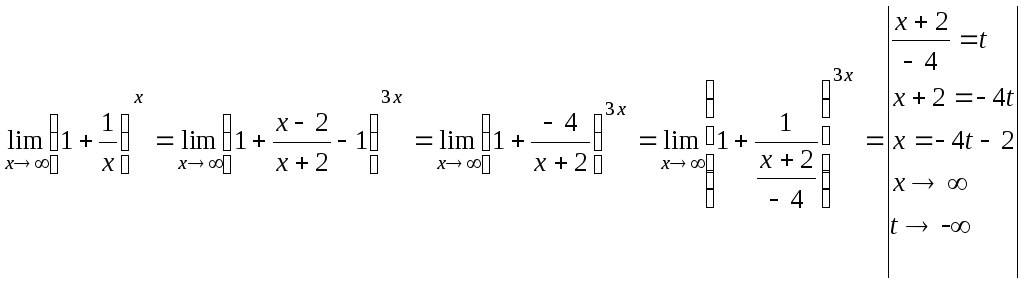 =
=

Тема: Сравнение бесконечно малых величин
Пусть даны две функции
![]()
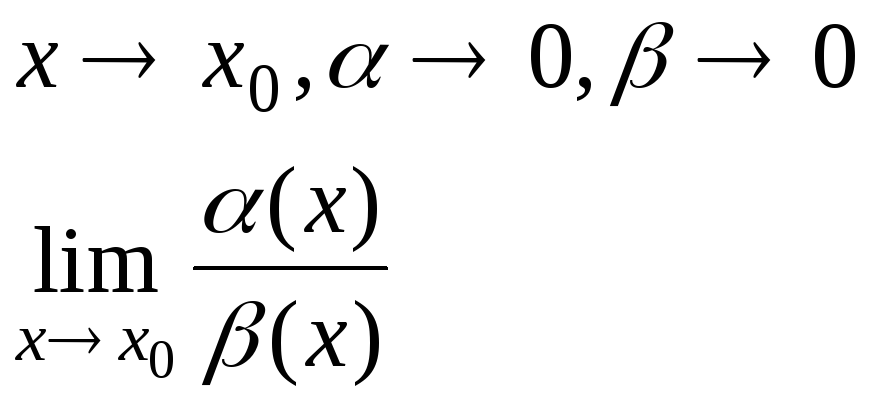
1) пусть этот предел равен случайному.
с≠0, тогда эти![]() ,
называются бесконечно малыми
,
называются бесконечно малыми
![]() одного
порядка малости или одного порядка.
одного
порядка малости или одного порядка.
Пусть с=1, тогда.
![]() называются
эквивалентами
называются
эквивалентами
![]()
![]()
![]() при
при
![]()
![]()
![]()
-
Пусть величина этого случайного предела =0, то
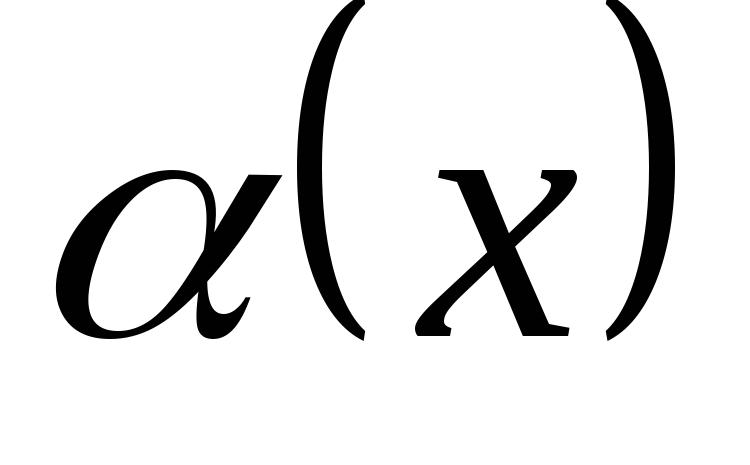 называют
называют
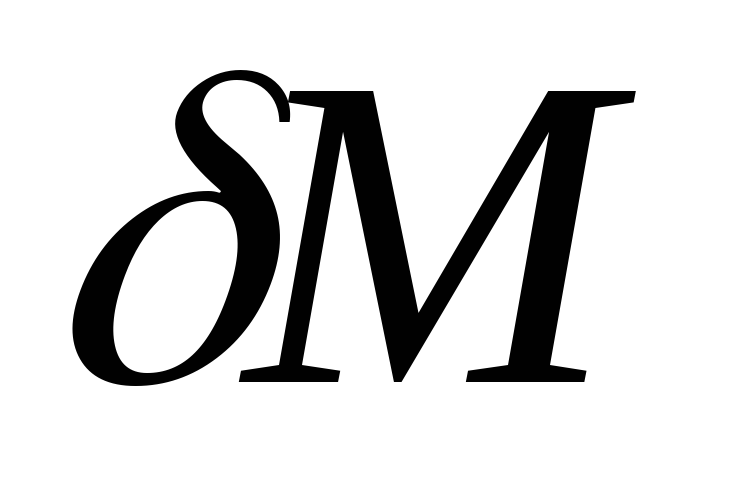 более высокого порядка по сравнению с
более высокого порядка по сравнению с
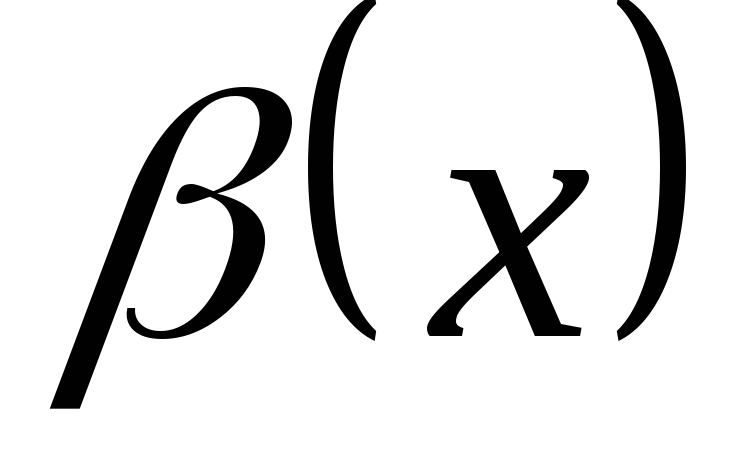 ,
,
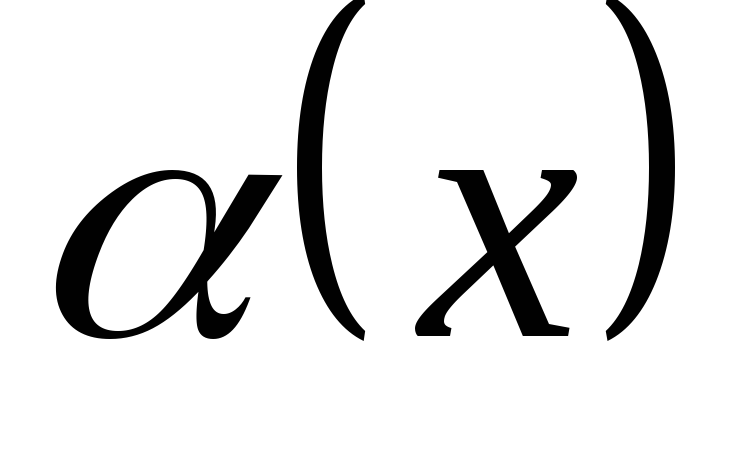 и
и
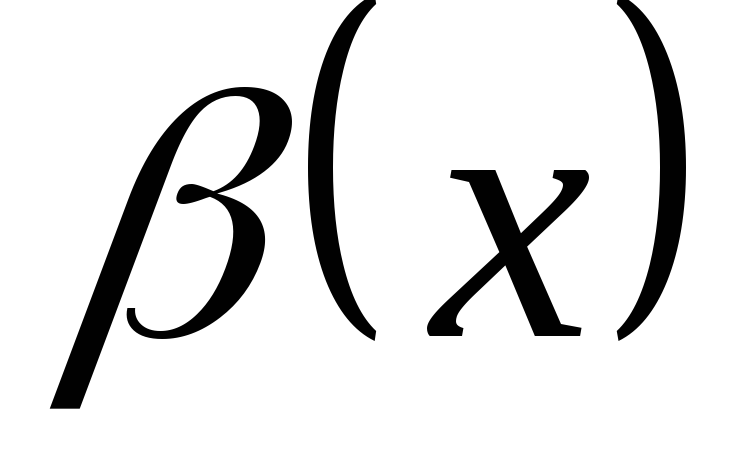 являются
являются
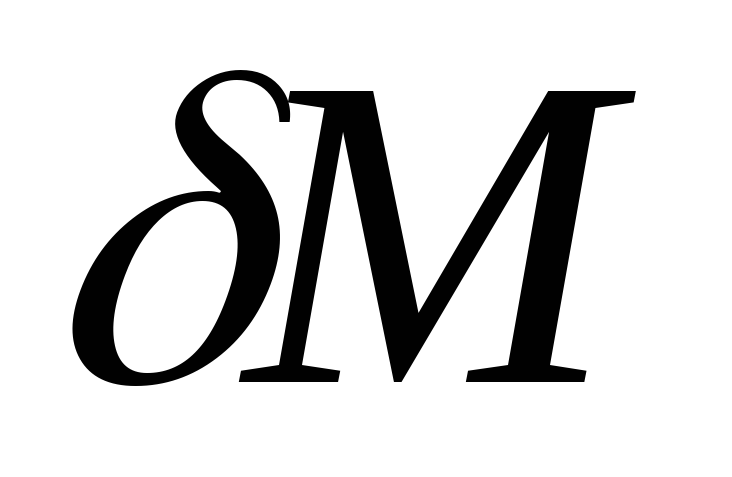 одного порядка, тогда
одного порядка, тогда
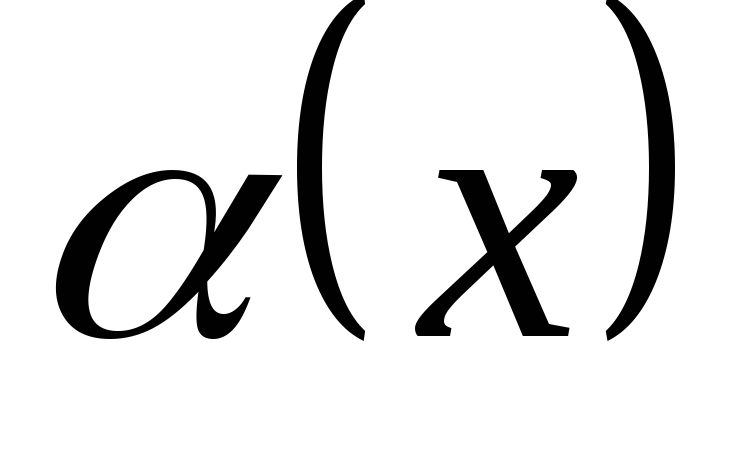 называют
называют
![]() катово порядка малости по сравнению с
катово порядка малости по сравнению с
![]() .
.

Непрерывность функции в точки и области
Пусть функция
![]() определяется в точке
определяется в точке
![]() и в некоторой ее окрестности.
и в некоторой ее окрестности.
Функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() если справедливо равенство
если справедливо равенство
![]()
Функция
![]() называется непрерывной, если
называется непрерывной, если
![]() то предел этой функции совпадает со
значением в точки
то предел этой функции совпадает со
значением в точки
![]()
Если
![]() ,
то
,
то
![]()
![]() (соответствующее
превращение функции)
(соответствующее
превращение функции)
![]()
Функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() если
если
![]() превращения
аргумента соответствует
превращения
аргумента соответствует
![]() превращения функции.
превращения функции.
Пусть
![]() ,
то
,
то
![]() ,
первое неравенство
,
первое неравенство
![]()
Если
![]() непрерывна в точке
непрерывна в точке
![]() ,
то предел этой функции при
,
то предел этой функции при
![]() вычисляется
подстановкой предельного значения
аргумента в функциональное выражение.
вычисляется
подстановкой предельного значения
аргумента в функциональное выражение.
Если
![]() непрерывна во всех точках области, то
она называется непрерывное в этой
области.
непрерывна во всех точках области, то
она называется непрерывное в этой
области.
Если
![]() непрерывна в некоторой области, то ее
график в этой области является сплошной
линией.
непрерывна в некоторой области, то ее
график в этой области является сплошной
линией.
Если график функции имеет разрывы, то такую функцию нельзя назвать непрерывной на этой области.
