Тема: Предел функции

Пусть имеется функция: , которая определяется в некоторой окрестности точки

Замечание: Существование функции в точке не обязательно.

Число b называют пределом функции при , если для любого положительного, заранее заданного, малого числа найдется такое число -зависящее от , что как только выполняется неравенство , сразу выполняется

f(x) y=f(x)

δ δ

0 x x₀ x

Пример:

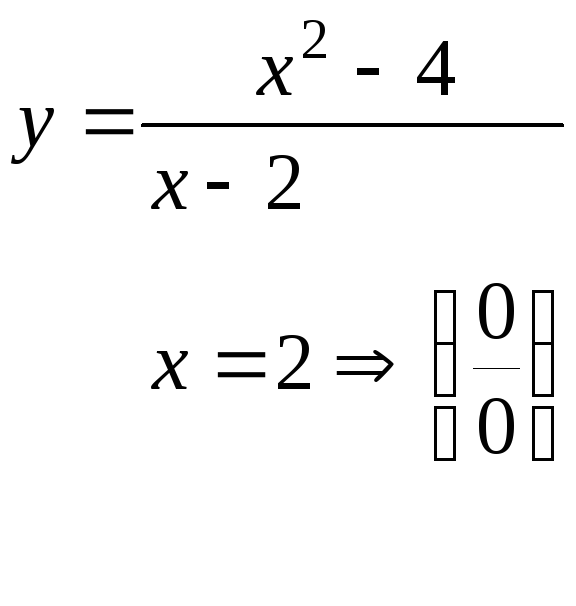
Lim

Функция в точке 2 не существует, а предел равен 4

Функция в точке может не существовать, а ее предел при может существовать.

Односторонние пределы

Пусть функция стремится к некоторому пределу b, причем , так что всегда принадлежит значению , тогда говорят, что b является левосторонним пределом функции , или пределом слева.

x₀ x

lim=b, то , всегда lim=b

-0 +0

Замечание: Если лево и правосторонние пределы при существуют и совпадают, то можно доказать, что в точки существует предел этой функции

Предел функции при бесконечном стремлении аргумента.

В определении предела функции мы не явно предполагали, что это конечное фиксированное число. Рассмотрим понятие предела функции

Число p называется пределом функции при , Если для любого положительного, малого, заранее заданного числа можно указать такое положительное число N(, что как только выполнится неравенство , сразу же выполнится неравенство

Пример:

y

ε₁ ε₂

0 N₁ N₂ x

Тема: Не ограниченные и ограниченные функции

y

0 1 x

1

Функция или является бесконечно большой величиной при ,

Если для любого положительного, большого, заранее заданного числа М>0 найдется такое положительное число , что как только выполняется неравенство , сразу выполняется неравенство

Функция называется ограниченной на некотором множестве значений аргумента ,

Если существует такое положительное число , для которого справедливо неравенство для любого из этого множества.

Если такого числа не существует на этом множестве, то -неограниченная функция на этом множестве.

y

4

1

1 2 x

є, у є

М=5,