Тема: свойства умножения матриц

1. А· В ≠В ·А - умножение матриц не коммутативно

2. Ассоциативность

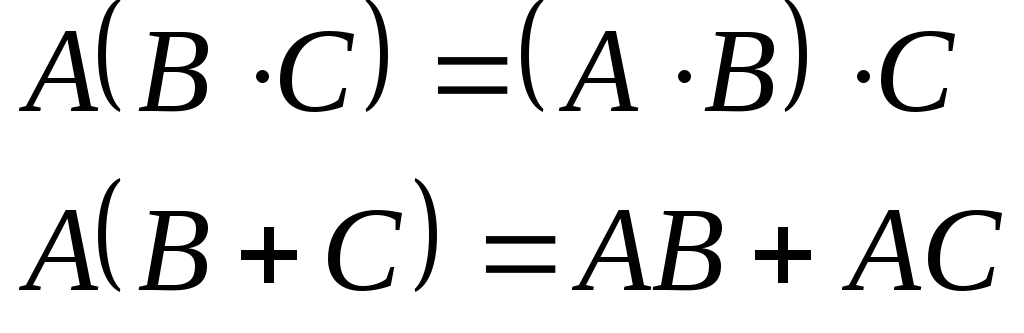
3. Распределительность

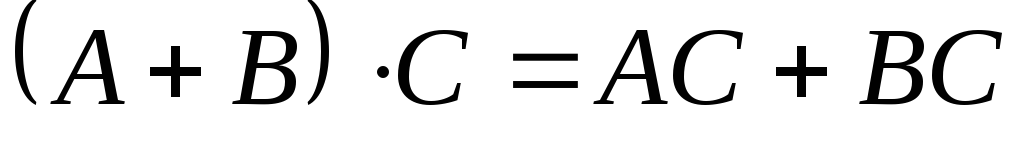
Тема: Обратная матрица и ее вычисление

А= квадратная матрица

ΔА =

Если определитель квадратной матрицы А не равен о, то матрица называется не вырожденной, если определитель равен 0, то матрица выражденная.

Единичной матрицей размерностью n, называется квадратная матрица вида:

Замечание: Единичная матрица играет такую же роль в теории матриц, как число единиц в теории чисел.

Пусть дана квадратная матрица А размерности n.

Матрица А^-1 такой же размерности называется обратной для матрице А если выполняется равенство:

Из определения следует, что эти две матрицы являются взаимообратными друг другу.

Условие существования обратной матрицы

Теорема: Если квадратная матрица не вырождена, то для нее существует обратная матрица.

Тема: Вычисление обратной матрицы

Пусть дана квадратная матрица А

1. Вычислить ее определитель ΔА

Если Δ =0, то обратная матрица не существует.

Если Δ≠0, то обратная матрица существует.

2. Нахождение союзной (присоединенной) матрицы

Обозначается А*

Матрица А* называется матрицей союзной матрицы А₁, если ее элементы есть алгебраические дополнения соответствующим элементам матрицы А.

3. Транспонирование союзной матрицы (А*)^т

4. Каждый элемент матрицы полученный в третьем пункте нужно разделить на определитель матрицы А(ΔА). Полученная матрица является обратной по отношению матрицы А

Тема: Решение систем линейных уравнений матричным способом

Рассмотрим тему на примере.

Пусть дана система трех линейных уравнений

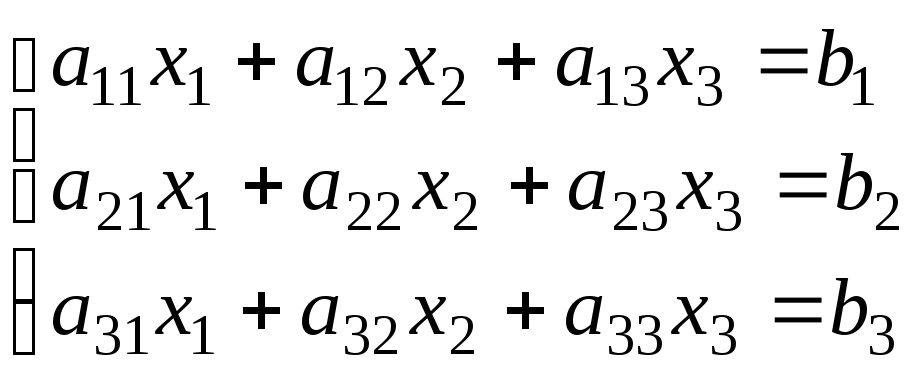
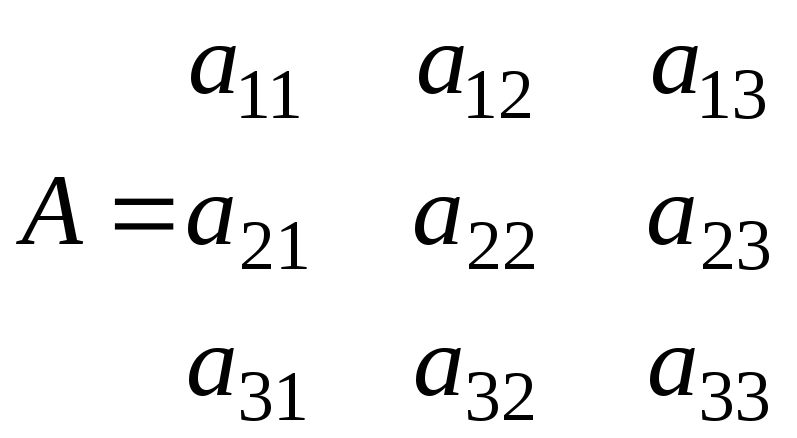
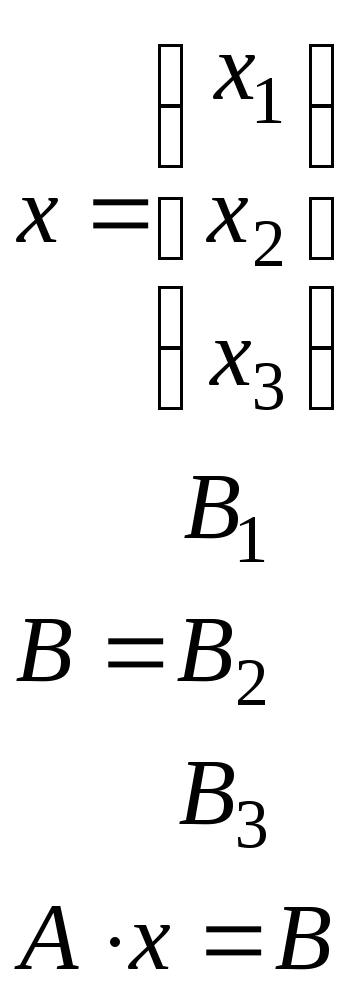
Пусть матрица А не вырождена, тогда для нее существует обратная матрица

Умножим две части уравнения слева на А

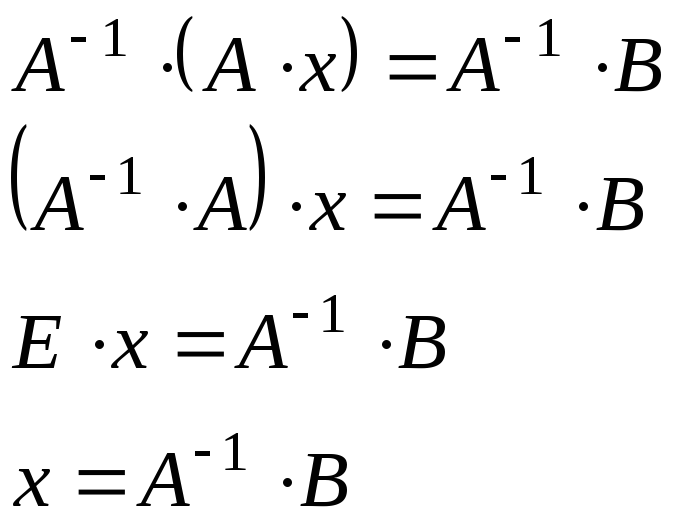
Формула решения системы линейных уравнений матричным способом

Пример: Решить систему матричным способом

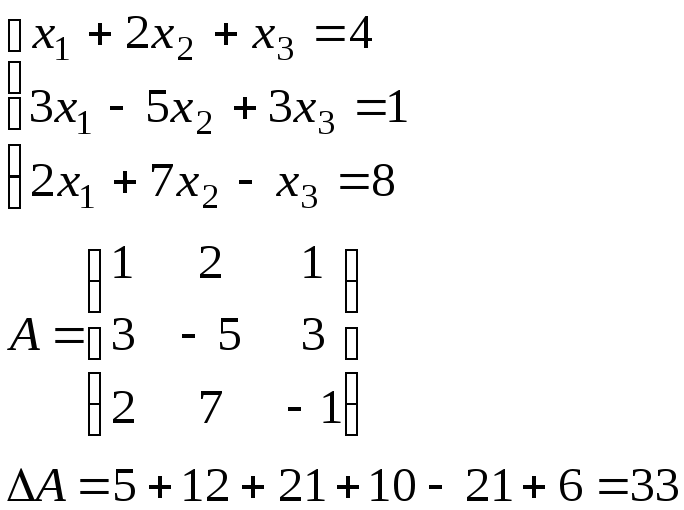
Матрица обратная А существует.

Находим союзную матрицу

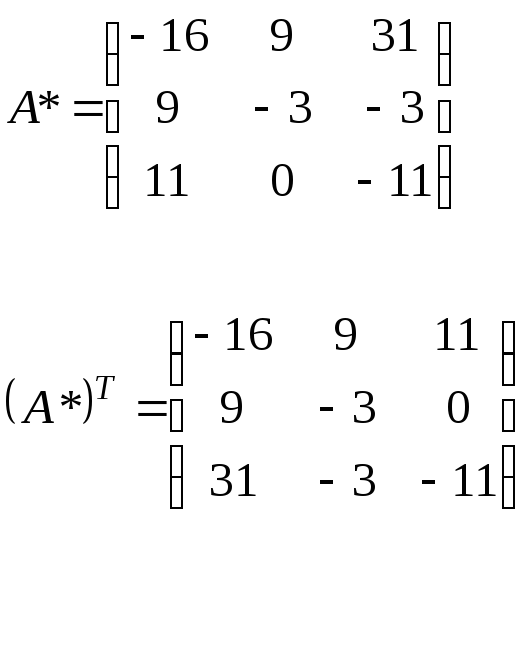
Ответ (1;1;1)

Тема: Дифференциальное исчисление

Функция и способы ее задавания.

Пусть некоторая величина может принимать значения из некоторых множеств действительных чисел.

є М

Если существует закон, по которому для любого из М можно указать единственное число у из некоторого множества N, то говорят, что на множестве M задана функция со значением, принадлежащим множеству N.

Замечание:

Функцией надо называть сам закон, а у – значением функции

х f у

аргумент функции

- значение функции

Замечание:

Из определения следует, что у должно быть единственным для заданного .

Пример: 1)

2)

Область определения функции называется множество всех значений , при которых у существует.

3)

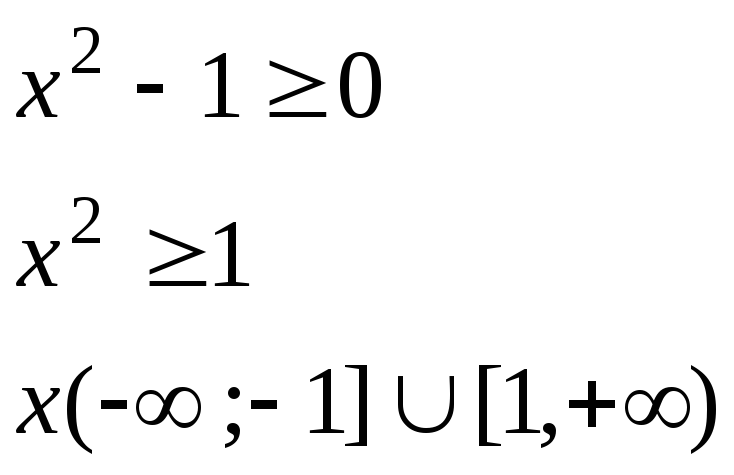
D(y); D () – функции

Е множество значений функции

Способы задания функции.

1. Табличный

X	X1	X2	X3	…..
Y	Y1	Y2	Y3	…..

2. Графический

y

0 x

3. Аналитический (задается с помощью одного или нескольких аналитических выражений)