Тема: Кривые второго порядка. Эллипс. Вывод канонического уравнения эллипса.

Эллипсом называется множество точек плоскости сумма расстояний, от которых до двух данных точек называемых фокусами постоянна.

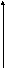y

M

F₁ 0 F₂ x

(для каждой токи эллипса), (а>0)

Вводим декартовую систему координат.

- фокусное расстояние эллипса

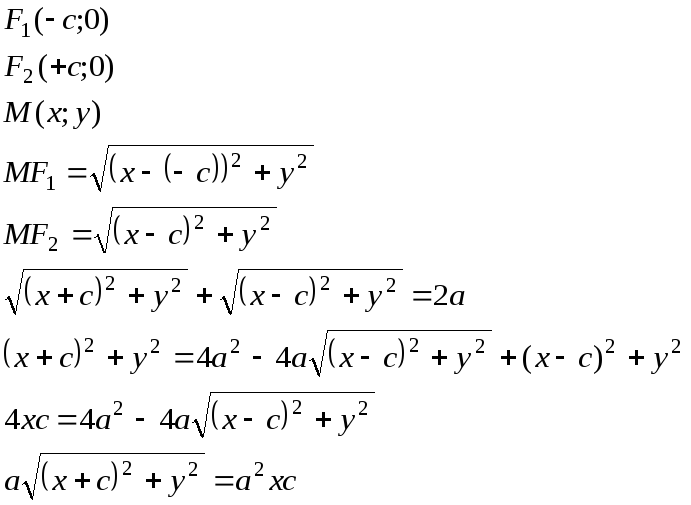
Еще раз возведем обе части в квадрат

Каноническое уравнение эллипса

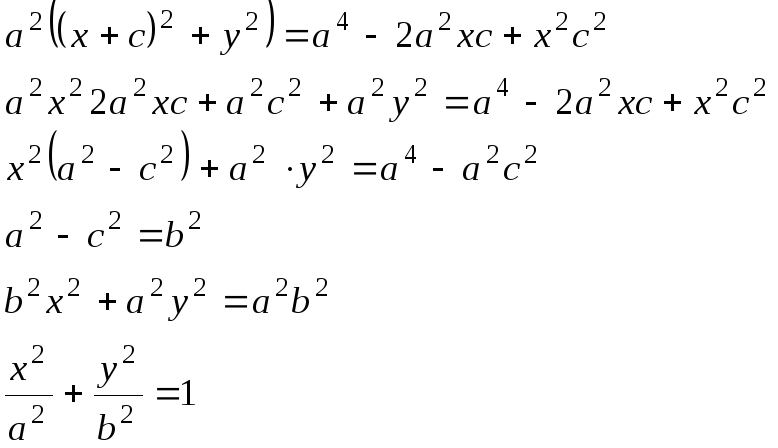
Можно доказать, что полученное равенство равносильно исходному, оно называется каноническим уравнением эллипса.

Тема: Исследование формы эллипса и его построения.

1. т.к координата (х;у) точек эллипса входят в уравнение во второй степени, это означает. Что эллипс симметричен, как относительно оси ох, так и оу

2. 

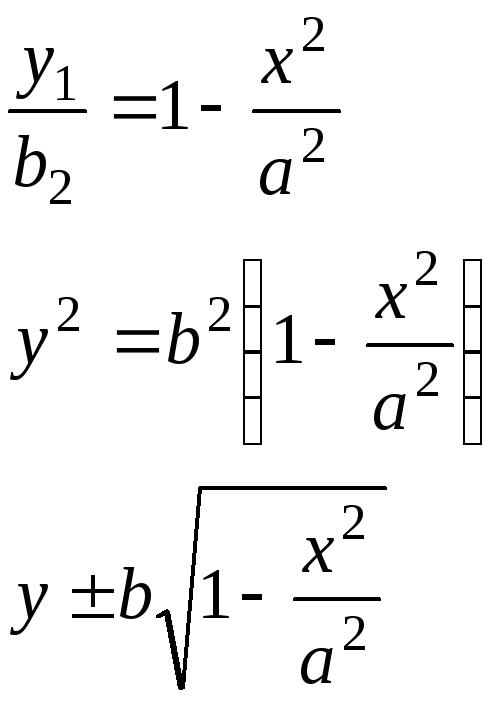
Будем исследовать это уравнение

1-

Вывод: от сюда следует, что эллипс существует не для любого х, а только на промежутке

принадлежит

3)

у принадлежит

y

b

-a c₁ c₂ a x

-b

4) Исследование формы кривой эллипса

- большая ось эллипса

- малая ось эллипса

5) Построение эллипса

y

A

B C

a

b 0 x

Тема: Эксцентриситет эллипса

Обозначение

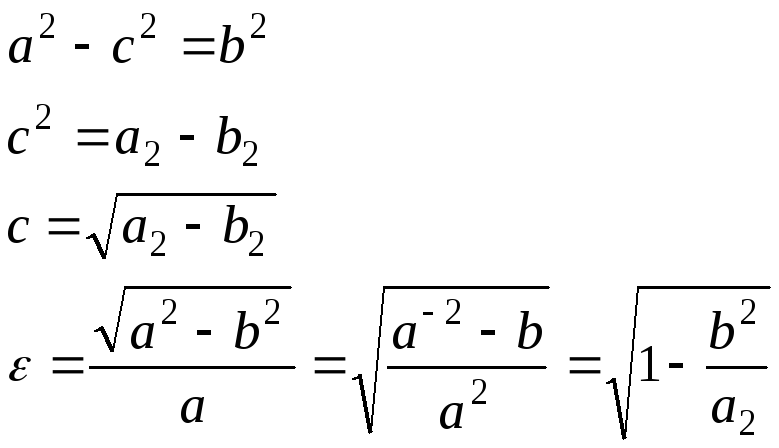
т.к. с, то

є

Если Эпсон → 0, то малая полуось по длине приближается к большой полуоси. Форма Эпсона все больше становится похоже на форму окружности и в пределе при получили окружность.

При →1 длина малой полуоси становится все меньше по сравнению с длиной большой полуоси. Эллипс становится более вытянутым и меньше похож на окружность.

Тема: Гипербола

Гиперболой называется множество точек в плоскости, для которых разность расстояний до двух данных точек называемых фокусами постоянна и равна 2а.

y

M

C₁ 2C C₂ x

Разность длин двух сторон треугольника

Каноническое уравнение гиперболы выводится также как и для эллипса

Каноническое уравнение гиперболы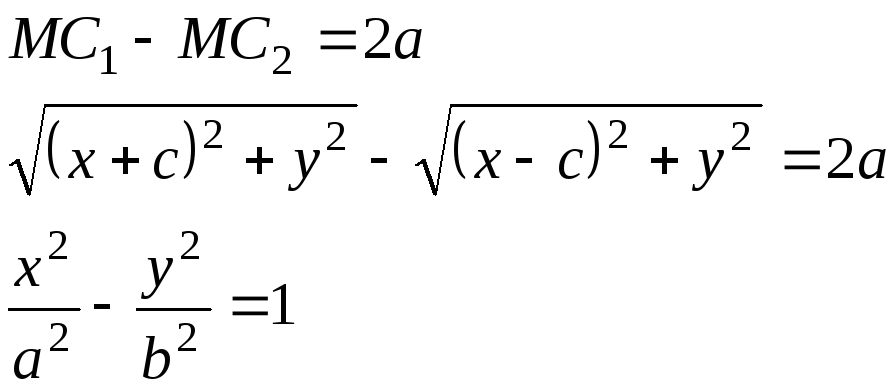

Тема: Исследование уравнения гиперболы

1)Гипербола симметрична относительно координатных осей.

2) Выразим у

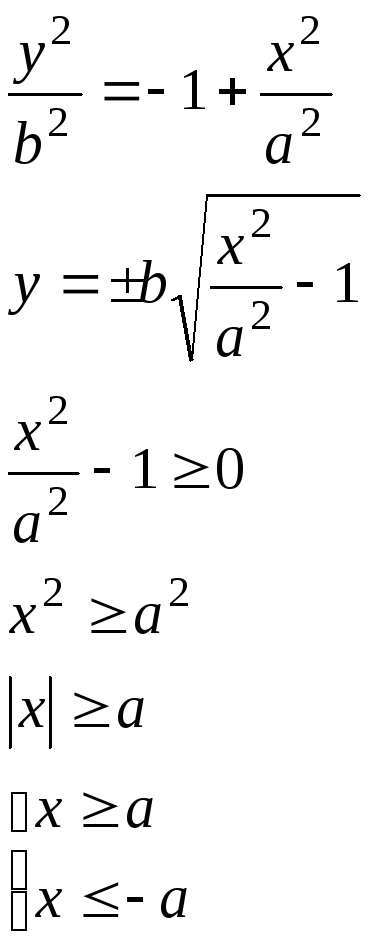
Вывод: Гипербола не существует для значений из промежутка

3)

существует при любом значении у.

Гипербола существует при любом значении у

4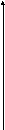) Определение формы гиперболы

Все действия выполняются в I четверти y

При

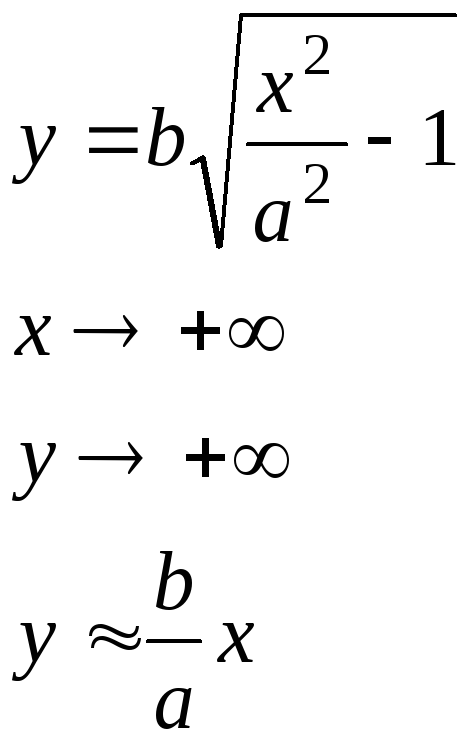
0 a x

Это прямая, к которой будет стремиться график гиперболы – асимптота гиперболы.

2. График гиперболы

b

C₁ C₂

-a a

-b