
- •1.5. Законы сохранения и изменения импульса и момента импульса в механике.
- •1.7. Законы сохранения и превращения энергии.
- •Раздел 2. Механические колебания /1а, 1б, 2б, 3б/
- •2.2. Затухающие колебания. Вынужденные колебания.
- •2.2.1.Затухающие колебания
- •2.2.1.1.Пружинный маятник
- •2.2.1.2.Режимы затухания
- •2.2.2. Вынужденные колебания
- •Раздел 3. Основы специальной теории относительности /1а, 1б, 3б/
- •3.1. Основы специальной теории относительности.
1.3.2. Законы Ньютона
Исаак Ньютон постулировал, что существуют инерциальные системы отсчёта. Это утверждение называют первым законом Ньютона. Этот закон не даёт указаний, сколько таких систем, как их искать, но заявляет сам факт их существования.
Внешнее воздействие
на любое тело, о котором говорилось
выше, следует как-то измерять. Величина,
именуемая силой,
вводится в качестве меры интенсивности
воздействия. Второй
закон Ньютона
гласит, что величина
силы, действующей на тело, равна быстроте
изменения импульса этого тела:
![]() .
Если записать это выражение как
.
Если записать это выражение как
![]() и назвать величину
и назвать величину![]() импульсом
силы, то
формулировка второго закона Ньютона
будет: импульс
силы, действующей на тело, равен изменению
импульса тела.
импульсом
силы, то
формулировка второго закона Ньютона
будет: импульс
силы, действующей на тело, равен изменению
импульса тела.
На одно и то же тело может одновременно оказываться несколько воздействий. В этом случае принцип суперпозиции гласит, что силы складываются как вектора (рис. 1.3.1).

Опыт показывает, что во всех случаях воздействие на какое-либо тело оказывает другое тело (или несколько тел), и это другое тело также подвергается воздействию со стороны первого тела. То есть любое воздействие является взаимодействием. Третий закон Ньютона гласит, что силы, с которыми воздействуют друг на друга взаимодействующие тела равны по величине и противоположны по направлению.
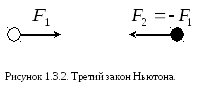
1.3.3. Виды сил в механике
Некоторые виды сил следует рассмотреть подробнее.
1.3.3.1. Сила тяготения
Закон всемирного тяготения гласит, что любые тела (материальные точки) притягиваются с силой, направленной вдоль линии, их соединяющей, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними (рис. 1.3.3):
![]()
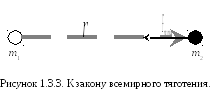
Можно доказать, что эта же формула верна не только для материальных точек, но и для любых сферически симметричных тел (сфер, шаров, сферических слоёв).
Как видно из
формулы, тело с массой m2
характеризуется только самой величиной
массы, а всё остальное относится только
к телу с массой m1
и пространственному расположению тел.
Можно считать, что это всё остальное
характеризует поле, предающее воздействие
от тела с массой
m1
на тело с массой m2.
Эта характеристика поля называется
напряженностью
![]() :
:
![]()
![]()
По второму закону
Ньютона любая сила, действующая на тело
массой m2:
![]() ,
следовательно
,
следовательно
![]() – напряженность гравитационного поля
равна ускорению, с которым будет двигаться
тело массой m2
по направлению к телу массой m1,
при условии, что других сил нет. Это
ускорение называется ускорением
свободного падения.
– напряженность гравитационного поля
равна ускорению, с которым будет двигаться
тело массой m2
по направлению к телу массой m1,
при условии, что других сил нет. Это
ускорение называется ускорением
свободного падения.
Заметим, что масса как мера инерции, входящая в уравнение для второго закона Ньютона, в точности равна массе как мере гравитации, входящей в закон всемирного тяготения. Это утверждение носит название принципа эквивалентности инертной и гравитационной масс и подтверждено с высокой точностью многочисленными экспериментами.
1.3.3.2. Сила тяжести
В тех задачах, где
изменение расстояния между центрами
гравитационно взаимодействующих тел
намного меньше самого расстояния,
величину изменения
![]() обычно можно считать несущественной и
принимать
обычно можно считать несущественной и
принимать
![]() для всех точек пространства, описываемых
в задаче. Поэтому просто записывают,
что сила тяжести
для всех точек пространства, описываемых
в задаче. Поэтому просто записывают,
что сила тяжести
![]()
1.3.4. Инерциальные и неинерциальные системы отсчета
Первый закон Ньютона утверждает, что существуют инерциальные системы отсчёта. Предположим, что нам известна одна инерциальная система отсчёта (нештрихованная – рис. 1.3.10).
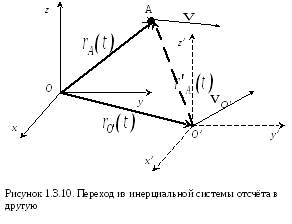
Как видно из рисунка
1.2.10:
![]() .
Поскольку это равенство выполняется
всегда, то и производные по времени от
обеих частей тоже равны:
.
Поскольку это равенство выполняется
всегда, то и производные по времени от
обеих частей тоже равны:
![]() ,
– или, что то же самое:
,
– или, что то же самое:
![]() .Аналогично,
взяв производную от скорости по времени,
получаем:
.Аналогично,
взяв производную от скорости по времени,
получаем:
![]() .
.
Предположим, что
в инерциальной системе отсчёта на тело
A
не действуют другие тела. Тогда это тело
движется в нештрихованной системе
отсчёта равномерно и прямолинейно и
![]() .
Если штрихованная система отсчёта также
является инерциальной, то и
.
Если штрихованная система отсчёта также
является инерциальной, то и
![]() ,
а следовательно и
,
а следовательно и
![]() .
То есть, система отсчёта, движущаяся
относительно инерциальной поступательно
без ускорения (иными словами, равномерно
и прямолинейно) сама является инерциальной.
.
То есть, система отсчёта, движущаяся
относительно инерциальной поступательно
без ускорения (иными словами, равномерно
и прямолинейно) сама является инерциальной.
1.3.5. Принцип относительности Галилея и преобразования Галилея
Если у нас обе
системы инерциальные (то есть
![]() )
и тело A
движется с ускорением
)
и тело A
движется с ускорением
![]() ,
то
,
то
![]() – ускорение инвариантно по отношению
к переходу из одной инерциальной системы
отсчёта в другую. Ускорения появляются
при наличии силы, действующей на тело
A:
– ускорение инвариантно по отношению
к переходу из одной инерциальной системы
отсчёта в другую. Ускорения появляются
при наличии силы, действующей на тело
A:
![]() .
То есть, при переходе из одной инерциальной
системы отсчёта в другую силы, действующие
на тела, не меняются. А следовательно,
выполняется принцип
относительности Галилея:
все механические явления в различных
инерциальных системах отсчёта протекают
одинаковым образом, вследствие чего
никакими механическими опытами невозможно
установить, покоится ли данная система
отсчёта или движется равномерно и
прямолинейно.
Поскольку
.
То есть, при переходе из одной инерциальной
системы отсчёта в другую силы, действующие
на тела, не меняются. А следовательно,
выполняется принцип
относительности Галилея:
все механические явления в различных
инерциальных системах отсчёта протекают
одинаковым образом, вследствие чего
никакими механическими опытами невозможно
установить, покоится ли данная система
отсчёта или движется равномерно и
прямолинейно.
Поскольку
![]() ,
то
,
то
![]() – преобразование
Галилея.
– преобразование
Галилея.
1.4.2. Основное уравнение динамики вращательного движения абсолютно твердого тела
Рассмотрим
материальную точку массой m,
которая находится в точке пространства
с радиус-вектором
![]() (рис.1.4.3),
движущуюся со скоростью
(рис.1.4.3),
движущуюся со скоростью
![]() .
Её импульс
.
Её импульс
![]() .
Пусть на это тело действует сила
.
Пусть на это тело действует сила
![]() .
.

Введем понятия:
момент силы
относительно точки
O:
![]() и момент
импульса относительно точки
O:
и момент
импульса относительно точки
O:
![]() .
На рис. 1.4.3 вектора
.
На рис. 1.4.3 вектора
![]() и
и
![]() направлены перпендикулярно поверхности
рисунка в сторону от читателя.
направлены перпендикулярно поверхности
рисунка в сторону от читателя.
Если взять производную от момента импульса по времени:
![]()
С учётом, что![]()
![]() ,
получаем
,
получаем
![]() .
По второму закону Ньютона
.
По второму закону Ньютона
![]() ,
поэтому получаем:
,
поэтому получаем:
![]() .
Это уравнение носит название основного
уравнения вращательного
движения.
Оно выполняется как для одной материальной
точки, так и для любого абсолютно твёрдого
тела, поскольку такое тело можно считать
состоящим из многих материальных точек.
.
Это уравнение носит название основного
уравнения вращательного
движения.
Оно выполняется как для одной материальной
точки, так и для любого абсолютно твёрдого
тела, поскольку такое тело можно считать
состоящим из многих материальных точек.
Моментом импульса тела относительно какой-либо оси называется проекция момента импульса относительно какой-либо точки указанной оси на эту ось.
1.4.2. Момент инерции твердого тела
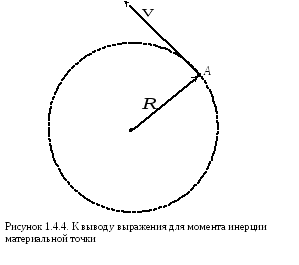
Пусть тело A
массой m
движется по окружности радиуса R
(рис. 1.4.4) с линейной скоростью
![]() .
Момент импульса этого тела
.
Момент импульса этого тела
![]() ,
где
,
где
![]() – угловая скорость движения тела A
по окружности. Если радиус окружности
не меняется, то и величина I=mR2
тоже не меняется. Следовательно,
– угловая скорость движения тела A
по окружности. Если радиус окружности
не меняется, то и величина I=mR2
тоже не меняется. Следовательно,
![]() ,
где
,
где
![]() – угловое ускорение. Видно, что
получающиеся формулы очень похожи на
выражения для импульса и для второго
закона Ньютона соответственно, только
вместо линейной скорости и ускорения
используются угловые скорость и
ускорение, а вместо массы – величина
I=mR2,
именуемая моментом
инерции материальной точки.
– угловое ускорение. Видно, что
получающиеся формулы очень похожи на
выражения для импульса и для второго
закона Ньютона соответственно, только
вместо линейной скорости и ускорения
используются угловые скорость и
ускорение, а вместо массы – величина
I=mR2,
именуемая моментом
инерции материальной точки.
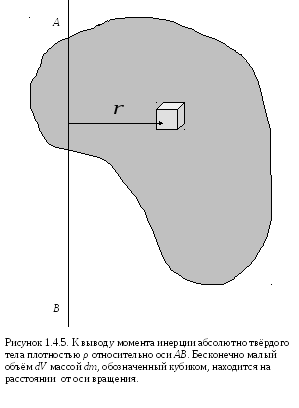
Если тело нельзя считать материальной точкой, но можно считать абсолютно твердым, то его момент инерции можно считать суммой моментов инерции бесконечно малых его частей, поскольку угловые скорости вращения этих частей одинаковы (рис. 1.4.5). Сумма бесконечно малых – интеграл:
![]()
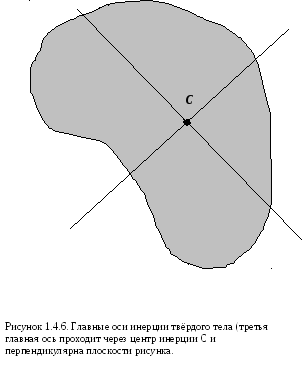
Для любого тела существуют оси, проходящие через его центр инерции, обладающие таким свойством: при вращении тела вокруг таких осей в отсутствии внешних воздействий оси вращения не меняют своего положения. Такие оси называются свободными осями тела. Можно доказать, что для тела любой формы и с любым распределением плотности существуют три взаимно перпендикулярные свободные оси, именуемые главными осями инерции тела (рис. 1.4.6). Моменты инерции тела относительно главных осей именуются главными моментами инерции тела.
Главные моменты инерции некоторых тел:

1.5.2. Импульс материальной точки и системы материальных точек.
Как было сказано
ранее, импульсом материальной точки
называется произведение её массы на
скорость:
![]() .
Для системы из N
материальных точек импульс системы
равен сумме импульсов материальных
точек, входящих в эту систему
.
Для системы из N
материальных точек импульс системы
равен сумме импульсов материальных
точек, входящих в эту систему
![]() .
Тело, которое нельзя считать материальной
точкой, можно разделить на бесконечно
малые объёмы и, перейдя от суммированию
к интегрированию, получить:
.
Тело, которое нельзя считать материальной
точкой, можно разделить на бесконечно
малые объёмы и, перейдя от суммированию
к интегрированию, получить:
![]() .
.
Поскольку
радиус-вектор центра масс любого тела
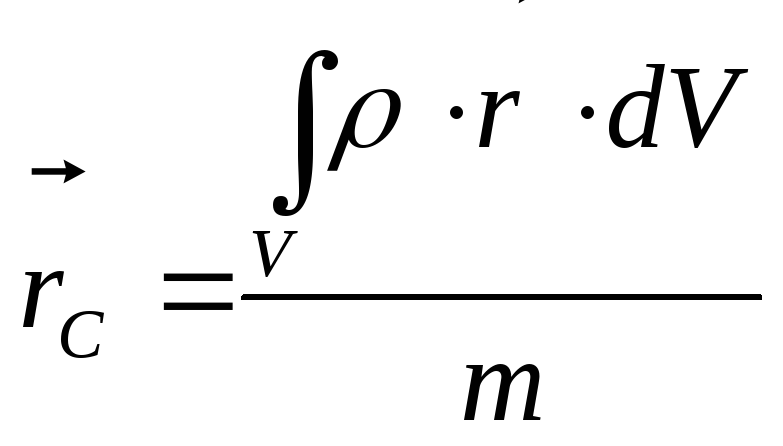 ,
то
,
то
![]() .
Взяв производную по времени от обеих
частей этого равенства, получаем
.
Взяв производную по времени от обеих
частей этого равенства, получаем
![]() .
То есть,
.
То есть,
![]() – импульс тела есть произведение массы
тела на скорость движения центра масс.
Таким образом, тело ведет себя как
материальная точка, обладающая всей
массой этого тела и находящаяся в центре
масс
– импульс тела есть произведение массы
тела на скорость движения центра масс.
Таким образом, тело ведет себя как
материальная точка, обладающая всей
массой этого тела и находящаяся в центре
масс
1.5. Законы сохранения и изменения импульса и момента импульса в механике.
1.5.1. Системы тел.
Любой набор тел именуется системой тел. Если на тела, входящие в систему, не действуют другие тела, не входящие в эту систему (или действие других тел на каждое тело скомпенсировано), то такая система тел называется замкнутой (закрытой, изолированной). Если действие других тел на тела, входящие в систему, не скомпенсировано, то такая система тел называется незамкнутой (открытой, неизолированной).
Система может состоять из одного тела.
1.5.3. Закон сохранения и изменения импульса материальной точки и системы материальных точек.
Рассмотрим замкнутую
систему тел – материальных точек (рис.
1.5.1). Поскольку для каждой силы
![]() (i
– номер тела, на которое действует сила,
j
– номер тела, со стороны которого
действует сила) существует
(i
– номер тела, на которое действует сила,
j
– номер тела, со стороны которого
действует сила) существует
![]() ,
то
,
то
![]() .
Таким образом, сумма всех сил, действующих
в замкнутой системе тел, равна нулю.
.
Таким образом, сумма всех сил, действующих
в замкнутой системе тел, равна нулю.

По второму закону
Ньютона
![]() .
Отсюда
.
Отсюда
![]() и, следовательно,
и, следовательно,
![]() – суммарный
импульс всех тел, входящих в замкнутую
систему есть величина неизменная.
Это выражает закон
сохранения импульса.
Этот закон действует только в инерциальных
системах отсчёта.
– суммарный
импульс всех тел, входящих в замкнутую
систему есть величина неизменная.
Это выражает закон
сохранения импульса.
Этот закон действует только в инерциальных
системах отсчёта.
Как было показано
ранее, координаты центра инерции
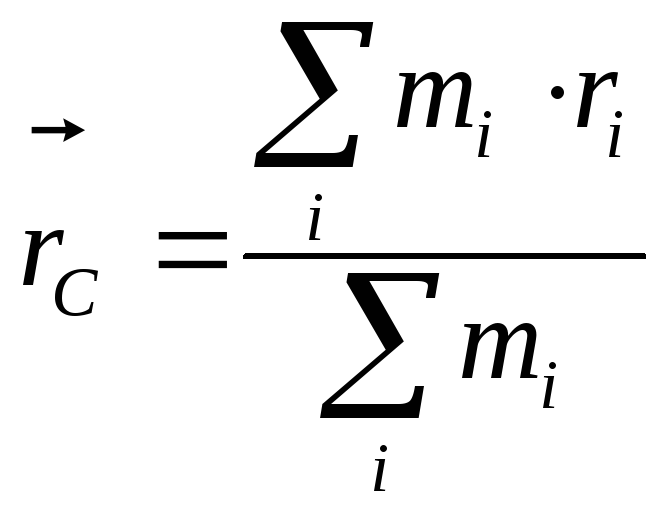 .
Если считать массы тел неизменными, то
можно взять производную
.
Если считать массы тел неизменными, то
можно взять производную
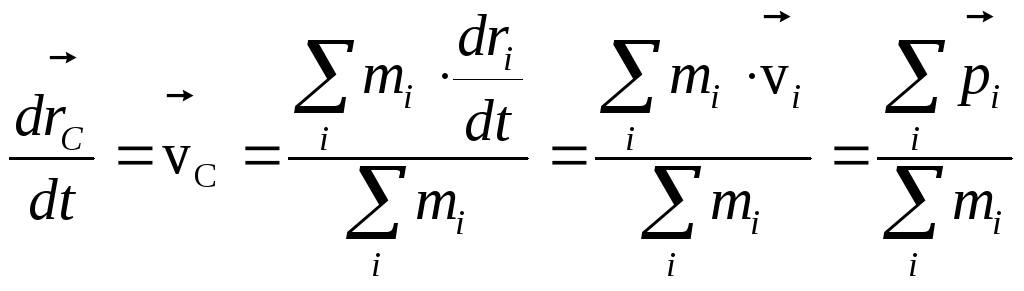 .
Из закона сохранения импульса получаем,
что в инерциальной системе отсчёта
скорость движения центра масс замкнутой
системы тел неизменна вне зависимости
от внутренних сил взаимодействия. А из
этого следует, что система
отсчёта, связанная с центром масс
замкнутой системы тел является
инерциальной.
.
Из закона сохранения импульса получаем,
что в инерциальной системе отсчёта
скорость движения центра масс замкнутой
системы тел неизменна вне зависимости
от внутренних сил взаимодействия. А из
этого следует, что система
отсчёта, связанная с центром масс
замкнутой системы тел является
инерциальной.
Если система тел
незамкнутая, то, кроме внутренних сил
![]() ,
действуют ещё и внешние силы
,
действуют ещё и внешние силы
![]() со стороны тел, не входящих в систему
(рис. 1.5.2). В этом случае полная сумма
всех сил
со стороны тел, не входящих в систему
(рис. 1.5.2). В этом случае полная сумма
всех сил
![]() .
.

1.5.4. Движение тел переменной массы
Представим себе
ракету массой M,
летящую равномерно и прямолинейно со
скоростью
![]() до момента времени t
(изображение (1) на рис. 1.5.1). В момент t
включается двигатель и за время Δt
ракета приобретает дополнительную
скорость
до момента времени t
(изображение (1) на рис. 1.5.1). В момент t
включается двигатель и за время Δt
ракета приобретает дополнительную
скорость
![]() (изображение (2) на рис. 1.5.3). Поскольку
скорость ракеты изменяется, можно
сказать, что на ракету действовала так
называемая реактивная
сила.
Заметим, что за это время масса ракеты
уменьшилась на ΔM
за счет вылета горючих газов.
(изображение (2) на рис. 1.5.3). Поскольку
скорость ракеты изменяется, можно
сказать, что на ракету действовала так
называемая реактивная
сила.
Заметим, что за это время масса ракеты
уменьшилась на ΔM
за счет вылета горючих газов.
При этом на ракету
могут действовать и иные силы (например,
сила сопротивления атмосферы), которые
на рис. 1.5.3 не показаны и равнодействующая
которых равна
![]() .
.
![]() ,
а
,
а
![]() .
Пусть из ракеты вылетают газы с постоянной
скоростью u м/с относительно ракеты в
количестве
кг/с. То есть
.
Пусть из ракеты вылетают газы с постоянной
скоростью u м/с относительно ракеты в
количестве
кг/с. То есть
![]() .
.
Рассмотрим систему отсчёта, движущуюся со скоростью ракеты в данный момент времени. В этом случае p = 0.
Если промежуток
времени устремить к нулю, то перейдём
к дифференциалам. В проекции на ось x
dp
= -
dt
u
+ mdv,
откуда
![]() ‑u + m
‑u + m![]() .
Отсюда получаем
.
Отсюда получаем
![]() – уравнение
Мещерского.
Величина
– уравнение
Мещерского.
Величина
![]() – реактивная сила, действующая на тело
переменной массы.
– реактивная сила, действующая на тело
переменной массы.
Если внешних сил
нет, то ‑u![]() .
При начальной скорости ракеты равной
нулю
.
При начальной скорости ракеты равной
нулю
![]() .
Отсюда
.
Отсюда
![]() .
.
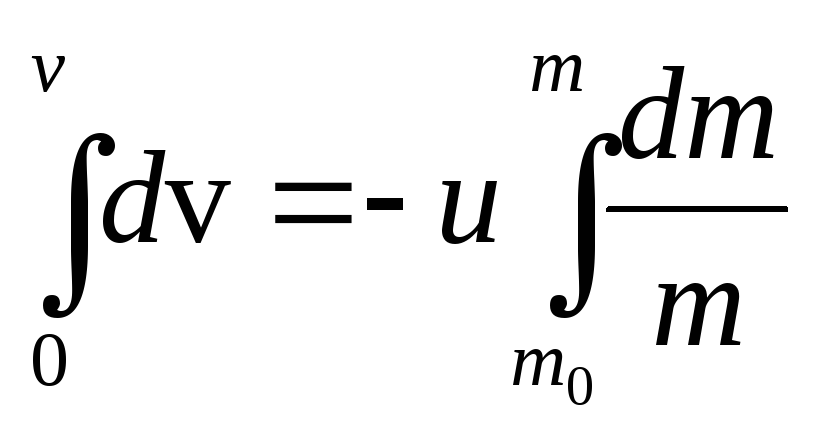
![]() начальная масса
ракеты.
начальная масса
ракеты.
![]() – формула
Циолковского.
– формула
Циолковского.
Таким образом,
![]() – максимальная скорость ракеты, где
– максимальная скорость ракеты, где
![]() -
масса топлива + масса окислителя.
-
масса топлива + масса окислителя.
1.5.5. Закон сохранения момента импульса.
Закон сохранения
импульса: для замкнутой системы
![]() .
Рассмотрим два взаимодействующих тела
(рис. 1.5.4).
.
Рассмотрим два взаимодействующих тела
(рис. 1.5.4).
![]()
![]()
Введем характеристику – момент импульса тела относительно точки 0.
![]()
![]()
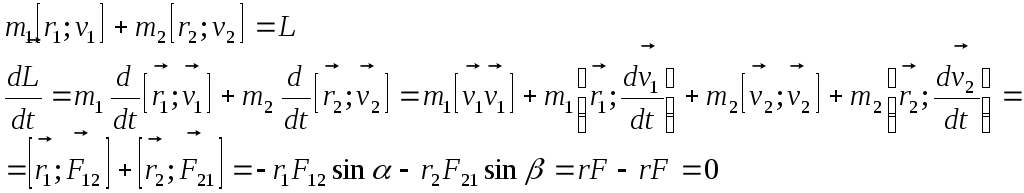
То есть
![]() - закон сохранения
момента импульса
- закон сохранения
момента импульса
Если через точку 0 провести произвольную ось, то момент импульса тела (системы тел) относительно этой оси будет равен проекции момента импульса тела (системы тел) относительно точки 0 на эту ось.
Величина
![]() - момент силы F
относительно точки.
- момент силы F
относительно точки.
Момент силы относительно оси – аналогично моменту импульса.
Для всех внутренних сил
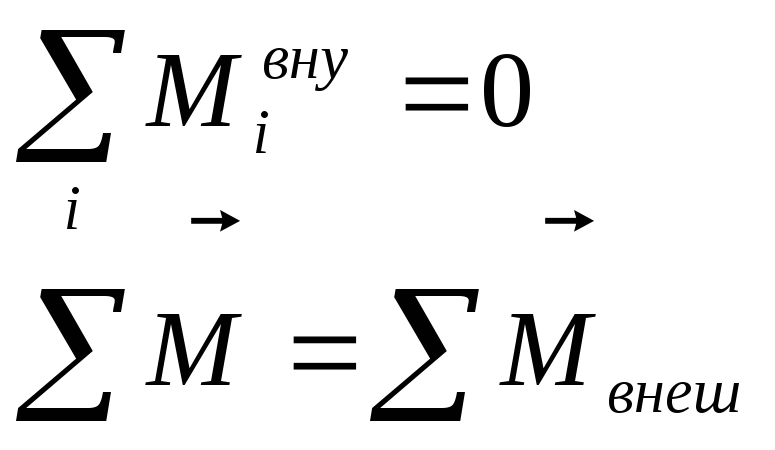
Т.о. получаем
![]() -
основное уравнение динамики вращ. дв-я
– аналог 2-го закона Ньютона.
-
основное уравнение динамики вращ. дв-я
– аналог 2-го закона Ньютона.
Под действием
![]() за
время dt
гироскоп получает приращение момента
импульса.
за
время dt
гироскоп получает приращение момента
импульса.
![]() - то есть ось
вращения гироскопа стала вращаться с
угловой скоростью
- то есть ось
вращения гироскопа стала вращаться с
угловой скоростью
![]() вокруг горизонтальной оси О – прецессия.
вокруг горизонтальной оси О – прецессия.
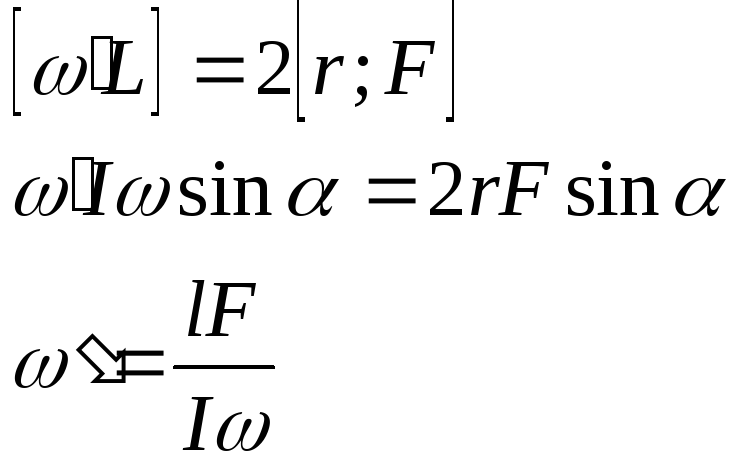
угловая скорость
прецессии не зависит от угла между
![]() и
и
![]()
