II. Второй вопрос задачи

Задачи этого типа предполагают, что имеет место некоторый факт, но этот факт мог быть проявлением одного из взаимоисключающих случаев (событий). Требуется выяснить вероятности случаев, предшествующих случившемуся факту. Эти задачи решаются с помощью формулы Байеса:

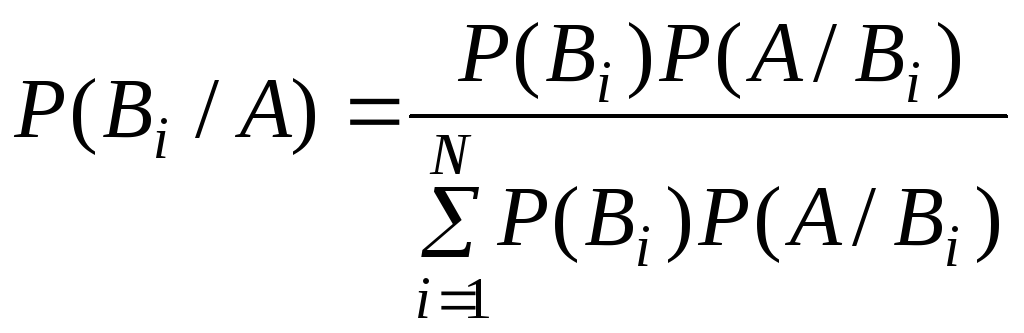
здесь А – событие, которое произошло;

B_i – событие, характеризующее случай номер "i";

P(B_i /А) – искомая вероятность, т.е. вероятность того, что имел место случай номер "i", при условии, что произошло событие А;

P(B_i) – вероятность появления случая номер "i" (или его доля в общей массе случаев);

N – количество возможных случаев;

P(A/B_i) – вероятность появления события А в ситуации, когда наблюдается случай номер "i" (называется условной вероятностью).

Пример 11. Из 30 курсантов, пришедших на экзамен по математике, 6 подго­товились отлично, 12 - хорошо, 6 - удовлетворительно и 6 понадеялись на удачу и приобретенные в течение семестра знания. Всего в экзаменационных билетах 105 вопросов, а в одном билете – три вопроса. Отлично подготовившиеся курсанты смогут ответить на все 105 вопросов, хорошо – на 80, удовлетворительно – на 60 и плохо подготовившиеся – на 20 вопросов. Первый курсант ответил на все три вопроса. Какова вероятность того, что он отличник?

Решение:

Обозначим события:

А – курсант ответил на 3 вопроса;

B₁ – отвечал курсант, подготовившийся на отлично;

B₂ – отвечал курсант, подготовившийся хорошо;

B₃ – отвечал курсант, подготовившийся удовлетворительно;

B₄ – отвечал курсант, к экзамену не готовившийся.

По классической схеме определения вероятности согласно условиям задачи получаем:

P(B₁)= (6 отличников из 30 курсантов); P(B₂)=; P(B₃)=; P(B₄)= .

Условные вероятности события А так же определяются по формуле класси­ческой вероятности. . Общее количество комбинаций вопросов в биле­тах n определится как число сочетаний по 3 из 105, т.е.

.

Отличник знает все вопросы, следовательно, его устраивают любые их комбина­ции. В этом случае M=N и вероятность ответа курсанта на все три вопроса, если он отличник, .

Курсанта, подготовившегося хорошо, устраивают только комбинации, обра­зованные из тех вопросов, которые он знает. Это число комбинаций определяется как число сочетаний по 3 из 80, т.е. и .

Курсанта, подготовившегося удовлетворительно, также устраивают только комбинации, образованные из тех вопросов, которые он знает. Это число комбина­ций определяется как число сочетаний по 3 из 60, т.е. и .

Аналогично рассчитывается и вероятность успешной сдачи экзамена плохо ­подготовившимся курсантом.

и .

Согласно условиям задачи следует найти , т.е. вероятность того, что отвечал отличник. По формуле Байеса получаем вероятность события B₁, при усло­вии, что наступило событие A:

.

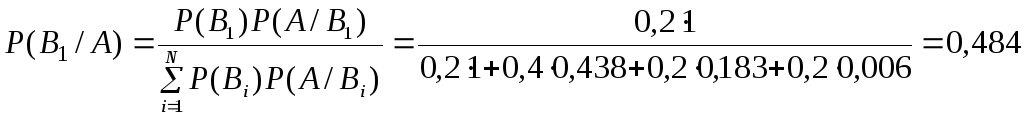Данный результат свидетельствует о том, что курсант, ответивший все три вопроса, скорее всего не является отличником!

Задачи 21-30

Для успешного ответа на вопросы этих задач необходимо ознакомиться с ли­тературой по определению вероятностей в случае многократного повторения оди­наковых испытаний [8, с.58-60].

Задачи этого типа предполагают, что происходит многократное повторение одного и того же эксперимента (подбрасывание монеты, стрельба по цели, покупка товара в магазине и т.п.) и в каждом конкретном опыте может произойти нужное событие, а может и не произойти.