II. Второй вопрос задачи

Если расчет коэффициента корреляции подтверждает существование линейной зависимости между признаками х и у, то уравнение этой зависимости можно определить на основе имеющихся статистических данных.

Искомое уравнение называется уравнением парной линейной регрессии и имеет вид:

где - среднее значение признака Y при определенном значении признака X;

b - свободный член уравнения;

а - коэффициент регрессии, характеризующий вариацию (изменение) Y, приходящуюся на единицу вариации X.

Коэффициенты уравнения регрессии рассчитываются из требования минимизации суммарных отклонений расчетного значения результативного признака от фактического. Параметр "b" вычисляют с помощью средних значений признаков х и у, подставляя их в выше приведенную формулу:

,

а параметр "a" из соотношения

.

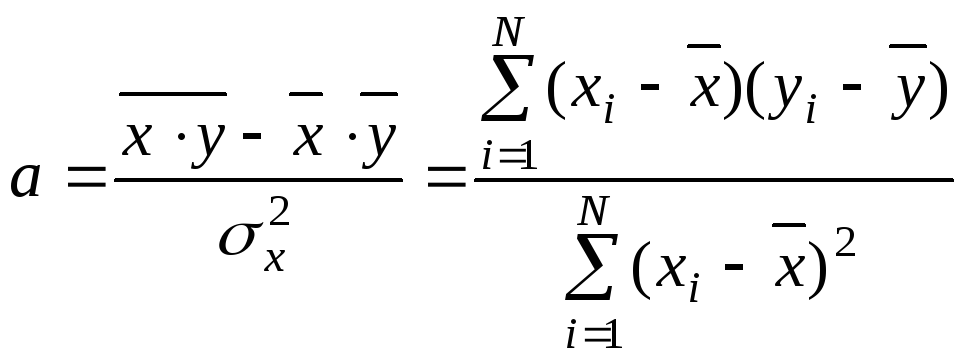Пример 25. Определить уравнение линейной регрессии по условиям примера 24.

Решение.

Для ответа на поставленный вопрос следует найти численные значения параметров а и b. В первую очередь рассчитаем параметр а. Для этого воспользуемся промежуточными результатами, полученными при расчете коэффициента корреляции в примере 24.Так как числитель расчетной формулы для параметра соответствует итоговой сумме значений в восьмой колонке, а знаменатель – итоговой сумме в шестой колонке, то получаем:

.

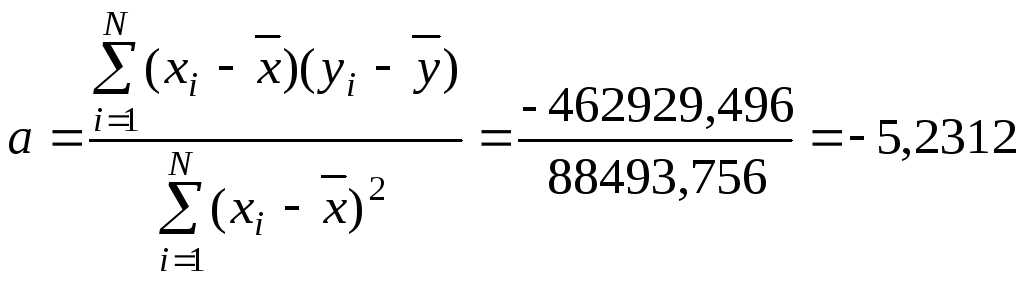Для расчета параметра b также воспользуемся результатами, полученными в примере 24. Согласно ранее выполненным расчетам средние значения признаков х и у равны соответственно =300,875 и =1222,25. С учетом полученного результата для параметра а получаем:

=1222,25 – (-5,2312)· 300,875=2796,187.

Зная числовые значения параметров а и b можно записать искомое уравнение регрессии:

.

III. Третий вопрос задачи

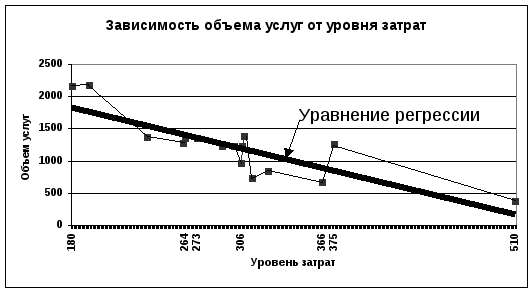
Ответ на этот вопрос предполагает, что будет нарисована система координат, в которой ось Х располагается горизонтально, а ось Y – вертикально.

В этой системе координат будут отмечены точки, соответствующие известным парам значений признаков x и y (например для каждой строки из таблицы примера 24). В качестве отмечающего знака можно использовать небольшой крестик, звездочку или другой символ.

Для определенного ранее уравнения регрессии следует рассчитать две точки, отметить их каким-либо другим знаком и провести через эти точки прямую линию. Например, если наносить такую прямую по данным примеров 24-25, то эти две точки целесообразно определить следующим образом.

1. Взять число 180 в качестве первого значения параметра х (из таблицы примера 24 легко убедиться, что это минимальное зафиксированное значение этого признака), подставить его в уравнение регрессии (см. пример 25) и вычислить соответствующее значение признака (y=1854,571).

2. Взять число 510 в качестве второго значения параметра х (из таблицы примера 24 легко убедиться, что это максимальное зафиксированное значение этого признака), подставить его в уравнение регрессии и вычислить значение признака (у=128,75).

В результате этих вычислений получены координаты двух точек, через которые можно провести линию регрессии на создаваемом рисунке. Для примеров 24-25 рисунок имеет следующий вид: