Задачи 51-60

Для успешного ответа на вопросы задачи необходимо ознакомиться с литературой по корреляционному и регрессионному анализу [8, с.97-117].

I. Первый вопрос задачи

В случае, когда статистическими методами исследуются два и больше числовых признака, часто возникает необходимость установить, как связаны между собой изменения этих признаков. Для решения этой проблемы в первую очередь следует определить сам факт существования такой связи. Для случая, когда исследуются два числовых признака (x и y), и есть основания полагать что искомая

зависимость будет линейной, используется коэффициент парной линейной корреляции (коэффициент Пирсона).

,

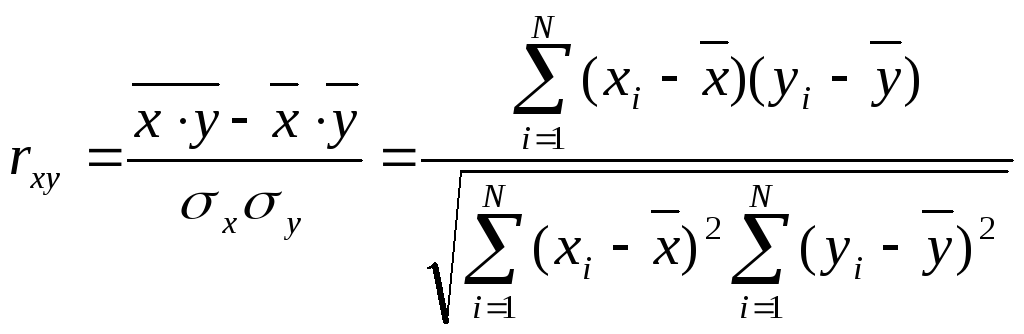где - среднее значение случайной величины, каждое отдельное значение которой равно произведению соответствующих значений x и y;

и - средние значения признаков x и y соответственно;

_x- среднеквадратическое отклонение признака x;

_y - среднеквадратическое отклонение признака у;

x_i и y_i - индивидуальные значения соответствующих признаков.

В зависимости от абсолютной величины коэффициента корреляции судят о тесноте связи между признаками х и у.

Значение коэффициента корреляции	Характер связи
от 0,00 до 0,30	крайне слабая или отсутствует
от 0,30 до 0,50	слабая
от 0,50 до 0,70	средняя
св. 0,70	сильная

Пример 24. Определить зависимость между затратами на содержание организаций и уровнем оказываемых ими услуг населению, численные значения которых приведены в таблице ниже.

Решение.

Решение такого типа задач может быть оформлено в виде таблицы. В колонке 2 таблице содержатся данные по уровню затрат на содержание организации (признак х), а в колонке 3 – данные по уровню услуг населению (признак у). После расчета итоговой суммы для каждой из колонок 2 и 3 и деления этих сумм на количество складываемых чисел получаем средние значения признаков =300,875 и =1222,25 (можно также воспользоваться правилам определения среднего, описанным ранее).

Для расчета коэффициента регрессии потребуется заполнить оставшиеся колонки этой таблицы.

В колонку номер 4 заносятся значения, соответствующие разности между индивидуальными значениями признака х (колонка 2) и средним значением этого признака (300,875). Так, например, для пятой строки это будет 301-300,875=0,125.

В колонку номер 5 заносятся значения, соответствующие разности между индивидуальными значениями признака у (колонка 3) и средним значением этого признака (1222,25). Так, например, для первой строки это будет 1224-1222,25=1,75.

№ п/п	Затраты руб./тыс. населе­ния xi	Уровень услуг руб./тыс. населе­ния уi			()2	()2	()·()
1	2	3	4	5	6	7	8
	292	1224	-8,875	1,75	78,766	3,063	-15,531
	510	378	209,125	-844,25	43733,266	712758,063	-176553,781
	366	662	65,125	-560,25	4241,266	313880,063	-36486,281
	308	1376	7,125	153,75	50,766	23639,063	1095,469
	301	1220	0,125	-2,25	0,016	5,063	-0,281
	314	730	13,125	-492,25	172,266	242310,063	-6460,781
	326	846	25,125	-376,25	631,266	141564,063	-9453,281
	306	960	5,125	-262,25	26,266	68775,063	-1344,031
	375	1252	74,125	29,75	5494,516	885,063	2205,219
	236	1366	-64,875	143,75	4208,766	20664,063	-9325,781
	264	1350	-36,875	127,75	1359,766	16320,063	-4710,781
	273	1352	-27,875	129,75	777,016	16835,063	-3616,781
	263	1276	-37,875	53,75	1434,516	2889,063	-2035,781
	307	1228	6,125	5,75	37,516	33,063	35,219
	193	2174	-107,875	951,75	11637,016	905828,063	-102670,031
	180	2162	-120,875	939,75	14610,766	883130,063	-113592,281
	4814	19559	0	0	88493,756	3349519,008	-462929,496

Числа из колонки 4, возведенные в квадрат, заносятся в колонку 6, а числа из колонки 5, так же возведенные в квадрат, заносятся в колонку 7. Произведение чисел из колонок 4 и 5 заносятся в колонку 8.

После заполнения колонок следует рассчитать итоговую сумму по каждой колонке и занести ее в соответствующую ячейку последней строки таблицы.

Теперь известны все промежуточные данные и можно определить коэффициент корреляции:

Коэффициент корреляции, рассчитанный для этого примера, будет равен

.

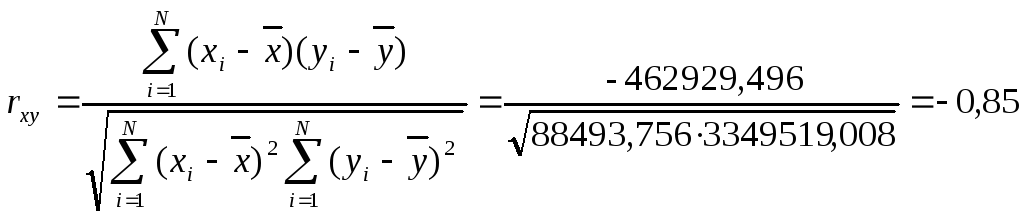Абсолютная величина коэффициента корреляции, в данном случае, свидетельствует о наличии сильной взаимосвязи между этими признаками, а его отрицательность - о том, что увеличение затрат на содержание организации (т.е. укрупнение организаций) не только не приводит к аналогичному увеличению уровня услуг населению, а наоборот – снижает его. Выгоднее использовать более мелкие организации.