Задачи 41-50

Для успешного ответа на вопросы задачи необходимо ознакомиться с литера­турой по статистике [8, с.70-88].

I. Первый и второй вопросы задачи

Обобщение результатов множества наблюдений и получение на их основе ко­личественных оценок наблюдаемых событий (фактов, характеристик) является од­ной из главных задач статистики.

К числу основных количественных оценок наблюдаемой статистическими методами случайной величины можно отнести среднее значение, дисперсию и среднеквадратическое отклонение. Расчеты этих характеристик подобны рассмотренным для задач 31-40. Единственное отличие заключается в том, что вместо вероятности используется относительная частота, т.е. отношение количества появлений интересующего наблюдателя события к общему количеству проведенных опытов (наблюдений).

Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот:

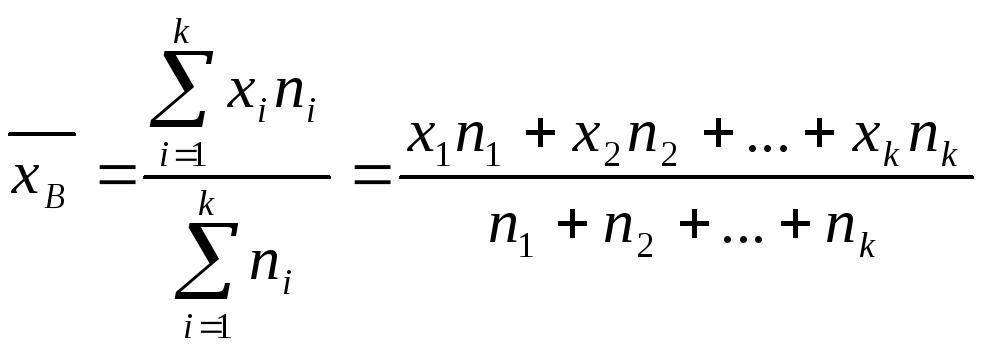
где х_i - варианты дискретного ряда или середины интервалов непрерывного ряда распределения (наблюдаемые значения случайной величины);

n_i – частоты вариант в вариационном ряду (количество наблюдений конкретного значения признака).

Выборочная дисперсия Dв характеризует рассеяние наблюдаемых значений количественного признака выборки относительно его среднего значения:

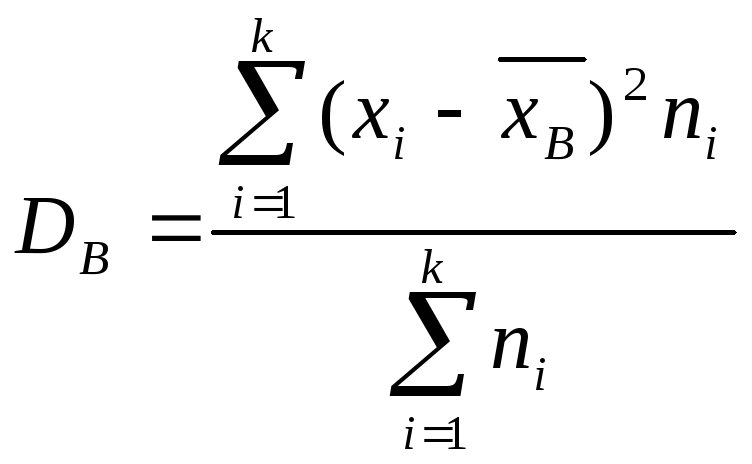
В некоторых случаях выборочную дисперсию удобно считать по формуле:

где, ;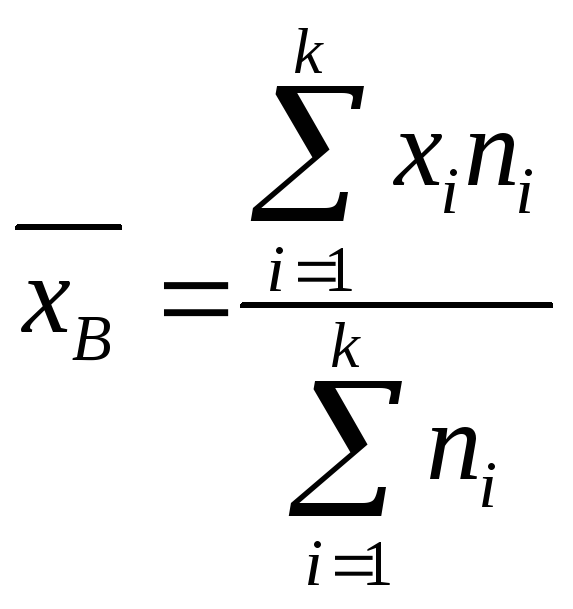

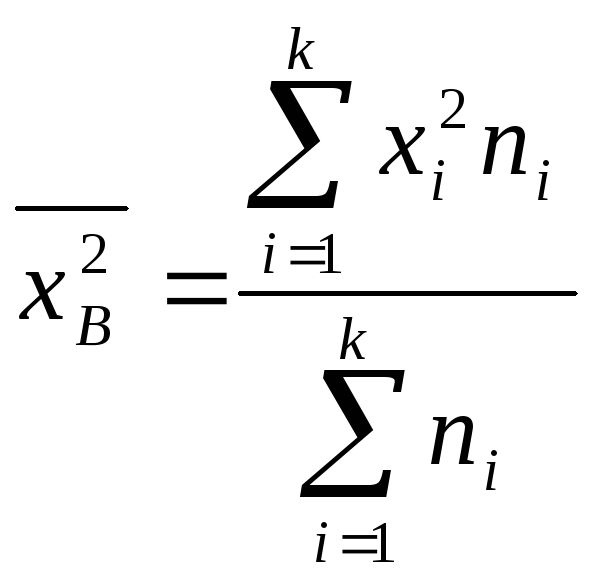х_i - варианты дискретного ряда или середины интервалов непрерывного ряда распределения (наблюдаемые значения случайной величины);

n_i – частоты вариант в вариационном ряду (количество наблюдений конкретного значения признака).

Среднеквадратическое отклонение s вычисляется по формуле:

_.

Пример. 22. Определить средний срок лишения свободы по данным выборочного исследования, результаты которого приведены в таблице, дисперсию и среднеквадратическое отклонение этого показателя.

Срок лишения свободы (в годах)	2-3	3-6	6-8	8-10	10-15
Количество осужденных (чел.)	4	4	35	45	12

Решение.

Вычислим среднее значение срока лишения свободы в каждом интервале:

Из приведенной таблицы определяем, что n₁=4, n₂=4, n₃=35, n₄=45, n₅=12.

Дальнейшее вычисление позволяет установить среднюю величину срока лишения свободы:

года

С учетом найденной величины среднего срока вычисляем дисперсию:

_{По известной дисперсии определим среднеквадратическое отклонение:}

II. Третий вопрос задачи

Полученные оценки числовых характеристик статистического распределения не являются абсолютно точными. В силу случайной природы наблюдаемых явлений, ошибок регистрации наблюдений и некоторых других причин всегда можно утверждать, что реальное значение отличается от рассчитанного. Для определения величины возможных отличий реального и расчетного значений используют понятие доверительного интервала, т.е. интервала в который с определенной вероятностью (задается заранее) попадет реальное значение.

При определении доверительного интервала для среднего арифметического по выборке применяется следующее двойное неравенство:

- Δ ≤ ≤ + Δ,

в котором Δ используется как предельно возможная ошибка:

,

здесь σ_в – среднеквадратическое отклонение статистического признака в выборке;

n – общее число наблюдений статистического признака;

t – нормированное отклонение (коэффициент доверия).

Коэффициент доверия играет важную роль в расчете возможной предельной ошибки. Если мы допускаем некоторую неизвестность относительно истинного значения оцениваемого параметра, то вполне естественно, что для повышения вероятности "захвата" этого значения определенным числовым диапазоном (доверительным интервалом) следует этот диапазон увеличивать. Вместе с тем истинное значение параметра не может принимать абсолютно любые значения и нет смысла делать доверительный интервал чрезмерно большим.

Коэффициент доверия t определяется в зависимости от задаваемой вероятности попадания истинного значения статистического показателя в доверительный интервал γ (доверительной вероятности) из следующей таблицы:

γ	t
0,6827	1
0,9	1,65
0,95	1,96
0,9545	2
0,99	2,58
0,9973	3
0,999.	3,29

Из этой таблицы, в частности вытекает, что если исследователь может себе позволить ошибиться в оценке с вероятностью 0,0027 (т.е. примерно в 27 случаях из десяти тысяч), то он может смело выбирать значение коэффициента доверия равное трем.

Пример. 23. Определить доверительный интервал для среднего срока лишения свободы по данным примера 22 при доверительной вероятности 0,9973.

Решение.

По таблице соотношений доверительной вероятности и коэффициента доверия находим, что при γ=0,9973 коэффициент доверия t равен 3. Используя результаты, полученные в примере 22 () получаем:

.

Таким образом, искомый доверительный интервал можно определить как

8,24 года ≤ ≤ 8,36 года.