Нахождение наибольшего и наименьшего значений функции, непрерывной на отрезке

Пусть – функция, непрерывная на некотором отрезке оси ох (рис. 5)

Ставится задача: указать схему нахождения тех точек отрезка оси ох, в которых функция достигает своего наибольшего значения и своего наименьшего значения , и найти эти и .

Сразу отметим, что такие точки на отрезке заведомо существуют (это доказано). А вот на интервале их может и не быть. То есть на интервале функция своих наибольшего и наименьшего значений может и не иметь. Например, функция на отрезке свое наименьшее значение достигает в точке , а свое наибольшее значение достигает в точке . А вот на интервале своих наибольшего и наименьшего значений функция , очевидно, не имеет (не достигает).

Вернемся к рис. 5, на котором изображена произвольная непрерывная на отрезке функция . Здесь достигается функцией на конце a отрезка , а – в точке x₁, являющейся одной из точек минимума функции. И вообще, очевидно, что и при любой другой форме графика непрерывной функции наибольшее и наименьшее значения достигаются ею на отрезке или в её точках экстремума, содержащихся на этом отрезке, или на концах отрезка. Отсюда вытекает следующая

схема нахождения и функции на отрезке :

1. Находим производную .

2. Находим принадлежащие отрезку точки, подозрительные на экстремум.

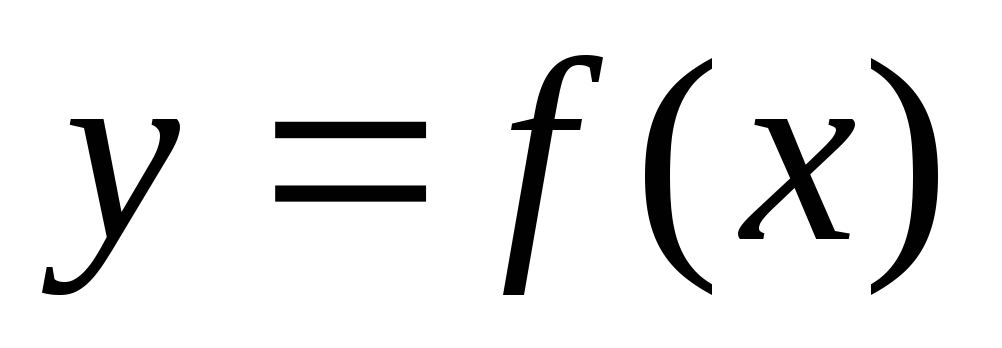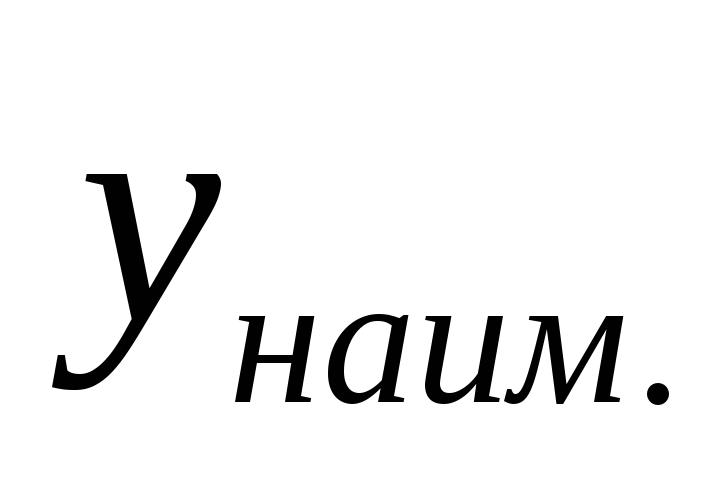3. Не исследуя этих точек, вычисляем значение функции во всех найденных подозрительных точках, а также на концах a и b отрезка . Из всех найденных значений y выбираем и . А заодно и устанавливаем, в каких точках отрезка эти и достигаются.

Пример 3. На отрезке найти наибольшее и наименьшее значения функции .

Решение. Реализуем изложенную выше схему.

1. Найдем :

.

2. Найдем на отрезке 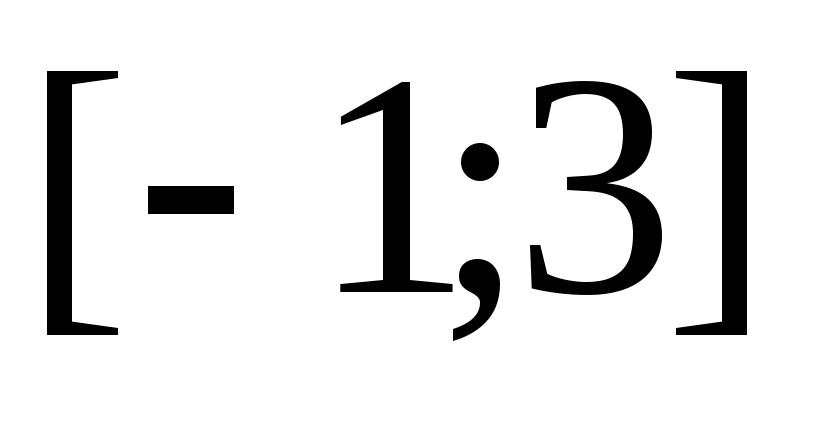точки (значения x), подозрительные на экстремум:

а) .

б) не существует  таких x нет.

На отрезке содержатся лишь две подозрительные на экстремум точки: это и .

3. Вычисляем значении функции в обеих найденных подозрительных точках, а также на концах отрезка, и выберем из найденных значений функции наибольшее и наименьшее:

; ; ;

Ответ: ; .

Выпуклость и вогнутость функции. Точки перегиба

Направление выпуклости кривой является важной характеристикой ее формы.

Понятие о выпуклости, вогнутости и точках перегиба функции дадим, исходя из рис. 6. На этом рисунке изображен график функции, выпуклой на интервале , вогнутой на интервале , и y которой точка x₀, разделяющая интервалы выпуклости и вогнутости, есть точка перегиба функции. Кстати, точка M₀ называется точкой перегиба графика функции (не путать точку перегиба функции x₀ и точку перегиба её графика M₀). Интервалы выпуклости, вогнутости и точки перегиба функции – важные характеристики любой функции, поэтому полезно уметь их находить.

Рассмотрим подробнее функцию на ее интервале выпуклости (рис. 7 (а)) и на ее интервале вогнутости (рис. 7 (б)).

Для выпуклой функции (рис. 7 (а)) касательная к ее графику в любой его точке расположена выше графика, причем с увеличением абсциссы x точки касания эта касательная поворачивается по часовой стрелке. Это значит, что с увеличением x угол наклона касательной к оси ох уменьшается. Но тогда уменьшается и угловой коэффициент касательной . А значит, с увеличением x уменьшается (убывает) равная ему производная функции . Но если некая функция убывает, то, как мы знаем, ее производная отрицательна. Значит, на всем интервале выпуклости функции .

Аналогичное рассуждение приводит к выводу, что если функция вогнута на некотором интервале (см. рис. 7 (б)), то для любого x из этого интервала (проведите это рассуждение самостоятельно).

Верно, естественно, и обратное: если на некотором интервале оси ох вторая производная функции положительна, то функция вогнута на этом интервале. А если эта производная отрицательна – то функция выпукла на указанном интервале.

Определение 3. Кривая обращена выпуклостью вверх на интервале , если все точки кривой лежат ниже любой ее касательной на этом интервале.

Определение 4. Кривая обращена выпуклостью вниз на интервале, если все точки кривой лежат выше любой ее касательной на этом интервале.

Кривая, обращенная выпуклостью вверх, будет называть выпуклой, а обращенную выпуклостью вниз – вогнутой.

Теорема 5: Если во всех точках интервала вторая производная f(x) отрицательна, т.е. , то кривая y=f(x) на этом интервале обращена выпуклостью вверх ( кривая выпукла )

Доказательство. Возьмем в интервале произвольную точку х=х₀ и проведем касательную к кривой в точке с абсциссой х=х₀.Теорема будет доказана, если мы установим, что все точки кривой на интервале лежат ниже этой касательной, т.е. что ордината любой точки кривой y=f(x) меньше ординаты y касательной при одном и том же значении х.

Уравнение кривой имеет вид

y=f(x).

Уравнение касательной к кривой в точке х=х₀ имеет вид

Откуда следует, что разность ординат кривой и касательной при одном и том же значении х равна

Применяя теорему Лагранжа к разности , получим:

,

( где с лежит между х₀ и х ). К выражению, стоящему в квадратных скобках, снова применим теорему Лагранжа, тогда

.

( где с₁ лежит между х₀ и с ).

Рассмотрим два случая:

1. Пусть х>x₀. Тогда x₀<c₁<c<x, поскольку . Учитывая этот факт и условие , получим .

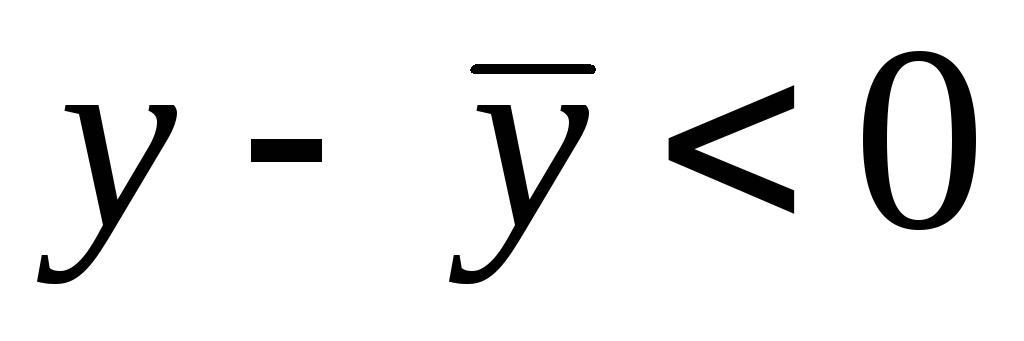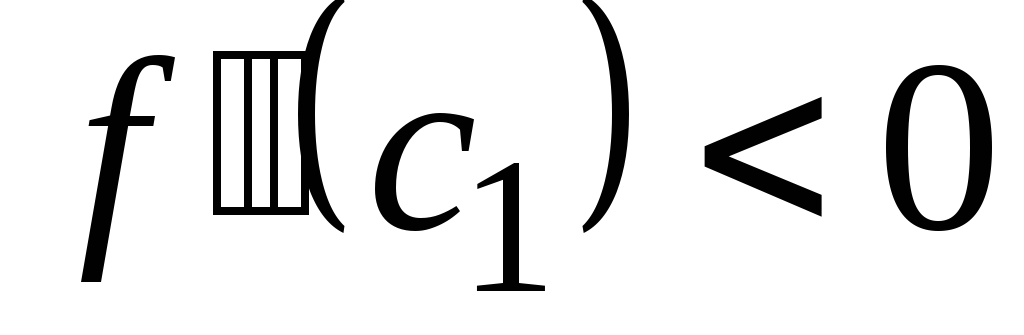2. Пусть х<x₀. Тогда x<c<c₁<x₀, поскольку . Учитывая этот факт и условие , получим .

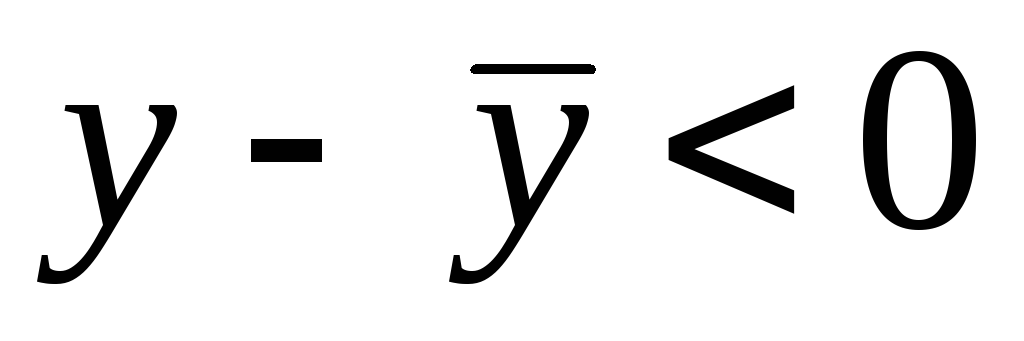Таким образом, мы доказали, что любая точка кривой лежит ниже касательной к кривой, каковы бы ни были значения х и х₀ на интервале . Что и означает, что кривая выпукла. Теорема доказана.

Аналогично доказывается теорема для случая вогнутой функции.

Теорема 6: Если во всех точках интервала вторая производная f(x) положительна, т.е. , то кривая y=f(x) на этом интервале обращена выпуклостью вниз ( кривая вогнута )

Теперь перейдем к точкам перегиба функции. Так как эти точки разграничивают интервалы выпуклости и вогнутости и, следовательно, не принадлежат ни тем, ни другим, то в точках перегиба вторая производная функции не может быть ни положительной, ни отрицательной. А значит, в этих точках она или равна нулю, или не существует.

Но не все точки x, в которых или не существует, непременно должны быть точками перегиба. Точками перегиба будут лишь те из них, в которых вторая производная меняет знак (с (+) на (–) или с (–) на (+)). Таким образом, точки оси ох, в которых или не существует, являются лишь подозрительными на перегиб. Окончательное выяснение сути этих точек производится после исследования знака второй производной слева и справа от каждой из них. Справедлива следующая

Теорема 7. Пусть кривая определяется уравнением y=f(x). Если или не существует и при переходе через значение x=a производная меняет знак, то точка кривой с абсциссой x=a есть точка перегиба.

Из всего сказанного вытекает

схема исследования функции на выпуклость-вогнутость и точки перегиба:

1. Находим область определения функции, а заодно устанавливаем интервалы ее непрерывности и точки разрыва (стандартное начало любого исследования функции).

2. Находим вторую производную .

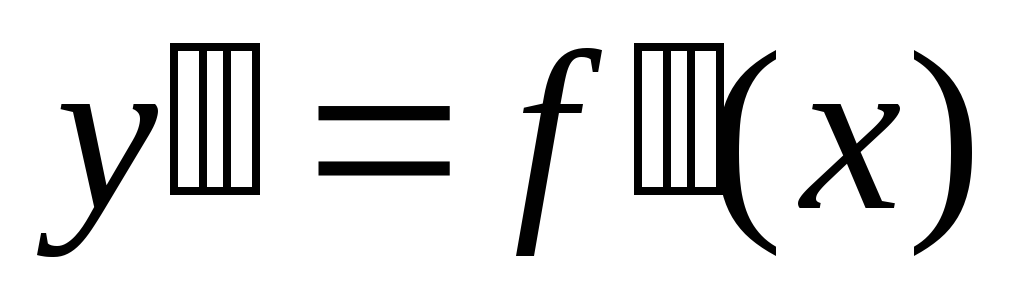3. Находим точки (значения x), подозрительные на перегиб. То есть находим те точки (значения x), в которых вторая производная функции или равна нулю, или не существует:

а)

б) не существует

4. Наносим все найденные подозрительные на перегиб точки на область определения функции (на ось ох) и отмечаем (например, дугами) интервалы, на которые разобьется этими дугами область определения функции. В каждом из этих интервалов выясняем знак второй производной . По установленным знакам этой производной отмечаем интервалы выпуклости и вогнутости функции ((–) – выпуклость, (+) – вогнутость), а также точки перегиба функции.

5. Вычисляем значения функции во всех найденных точках ее перегиба и находим тем самым точки перегиба графика функции.

Пример 4. Исследовать на выпуклость-вогнутость и точки перегиба функцию (в примере 2 она уже исследовалась на возрастание-убывание и точки экстремума).

Решение. Реализуем изложенную выше схему.

1. Функция определена, а следовательно и непрерывна для любых x от до .

2. Найдем :

.

3. Найдем точки (значения x), подозрительные на перегиб:

а) .

б) не существует  таких x нет.

4. Нанесем на ось ох найденную подозрительную на перегиб точку . Ось ох (область определения функции) разобьется этой точкой на два интервала:

Определяем знаки второй производной в этих интервалах (они отмечены на рис. выше). Тем самым устанавливаем интервалы выпуклости (знак ) и вогнутости (знак ) , а также устанавливаем, что – точка перегиба функции.

5. Вычисляем значение функции в точке ее перегиба и тем самым определим точку перегиба графика функции (она указана на рис. 4).