Практическая работа 2: сТруктуры на множествах
-
Краткие сведения из теории
Рассмотрим
два множества
![]() и
и
![]() .
Пусть
.
Пусть
![]() элементы
множества
элементы
множества
![]() ;
;
![]() элементы
множества
элементы
множества
![]() .
Из элементов этих множеств образуем
всевозможные пары
.
Из элементов этих множеств образуем
всевозможные пары
![]() ;
такие пары элементов называются
упорядоченными парами. Первый элемент
упорядоченной пары называется первой
компонентой, второй элемент – второй
компонентой.
;
такие пары элементов называются
упорядоченными парами. Первый элемент
упорядоченной пары называется первой
компонентой, второй элемент – второй
компонентой.
Декартовым
произведением
![]() множеств
множеств
![]() и
и
![]() называется множество всех упорядоченных
пар, у которых первая компонента
принадлежит множеству
называется множество всех упорядоченных
пар, у которых первая компонента
принадлежит множеству![]() ,
вторая компонента – множеству
,
вторая компонента – множеству
![]() .
.
Другими
словами,
![]() .
.
Бинарное
отношение.
Пусть
![]() два
множества. Бинарным отношением &
называется некоторое подмножество
декартова произведения
два
множества. Бинарным отношением &
называется некоторое подмножество
декартова произведения
![]() .
Бинарное
отношение –
это отношение, устанавливающее связь
между парами элементов двух разных
множеств или одного и того же множества.
Бинарное
отношение в дальнейшем будем обозначать
символом &. Бинарное отношение &
можно задавать либо путем его описания,
либо указанием множества всех пар
элементов, находящихся в отношении &.
В общем виде бинарное отношение &
можно задать так:
.
Бинарное
отношение –
это отношение, устанавливающее связь
между парами элементов двух разных
множеств или одного и того же множества.
Бинарное
отношение в дальнейшем будем обозначать
символом &. Бинарное отношение &
можно задавать либо путем его описания,
либо указанием множества всех пар
элементов, находящихся в отношении &.
В общем виде бинарное отношение &
можно задать так:
&![]() .
.
Например,
если множества
![]() {мышь,
курица, заяц},
{мышь,
курица, заяц},
![]() {кошка,
собака, лисица, волк}, то бинарное
отношение & – «быть съеденным» задается
так: &={(мышь, кошка), (мышь, лисица),
(курица, собака), (курица, лисица), (курица,
волк), (заяц, собака), (заяц, лисица), (заяц,
волк)}.
{кошка,
собака, лисица, волк}, то бинарное
отношение & – «быть съеденным» задается
так: &={(мышь, кошка), (мышь, лисица),
(курица, собака), (курица, лисица), (курица,
волк), (заяц, собака), (заяц, лисица), (заяц,
волк)}.
Например,
если числовое множество
![]() ,
то бинарное отношение & – «быть
делителем», построенное на множестве
,
то бинарное отношение & – «быть
делителем», построенное на множестве
![]() ,
выглядит так: &
,
выглядит так: &![]()
Функция.
Пусть
![]() множество
действительных чисел. Функцией
множество
действительных чисел. Функцией
![]() называется закон, по которому каждому
числу
называется закон, по которому каждому
числу
![]() ставится в соответствие единственное
действительное число
ставится в соответствие единственное
действительное число
![]() .
При этом в записи:
.
При этом в записи:
![]() символ
символ
![]() называется аргументом, символ
называется аргументом, символ
![]() –
значением функции, символ
–
значением функции, символ
![]() именем функции. Множество
именем функции. Множество
![]() называется областью определения функции
и обозначается
называется областью определения функции
и обозначается
![]() .
Множество всех значений
.
Множество всех значений
![]() называется областью значений функции
и обозначается
называется областью значений функции
и обозначается
![]() .
Важным понятием для функции является
ее график. Графиком
функции
.
Важным понятием для функции является
ее график. Графиком
функции
![]() называется точек на плоскости вида
называется точек на плоскости вида
![]() ,
где
,
где
![]() .
Существует четыре способа задания
функции:
.
Существует четыре способа задания
функции:
-
аналитический; функция задается одной или несколькими способами;
-
графический; функция задается своим графиком;
-
табличный; функция задается таблицей значений аргумента
 и
функции
и
функции
 ;
;
-
компьютерный; составляется компьютерная программа, предусматривающая вывод функции либо одним из трех указанных выше способов, либо передающая функцию на другую компьютерную программу.
Какой способ задания является предпочтительным? На этот вопрос нельзя дать однозначный ответ, так как каждый способ имеет свои преимущества и недостатки.
Бинарное
отношение и функция.
Пусть
функция
![]() имеет область определения
имеет область определения
![]() и область значений
и область значений
![]() .
Согласно определению функции для каждого
значения аргумента
.
Согласно определению функции для каждого
значения аргумента
![]() мы находим единственное значение функции
мы находим единственное значение функции
![]() .
Другими словами, получаем упорядоченную
пару
.
Другими словами, получаем упорядоченную
пару
![]() ,
принадлежащую декартову произведению
,
принадлежащую декартову произведению
![]() .
Это означает, что любая функция
.
Это означает, что любая функция
![]() порождает некоторое бинарное отношение
&.
порождает некоторое бинарное отношение
&.
А
верно ли обратное утверждение? Можно
ли утверждать, что любое бинарное
отношение порождает функцию? В общем
случае это не так. Например, бинарное
отношение &![]() не порождает функцию, потому что одному
и тому же значению аргумента
не порождает функцию, потому что одному
и тому же значению аргумента
![]() соответствует два значения функции
соответствует два значения функции
![]() и
и
![]() ;
этого по определению функции быть не
должно. Поэтому, чтобы бинарное отношение
& порождало бы некоторую функцию,
нужно, чтобы первые компоненты & были
различны между собой.
;
этого по определению функции быть не
должно. Поэтому, чтобы бинарное отношение
& порождало бы некоторую функцию,
нужно, чтобы первые компоненты & были
различны между собой.
Производная.
Пусть функция
![]() определена на множестве
определена на множестве
![]() ,
точки
,
точки
![]() .
Приращением аргумента
.
Приращением аргумента
![]() называется разность
называется разность
![]() .
Ясно, что
.
Ясно, что
![]() .
Приращением функции
.
Приращением функции
![]() называется разность
называется разность
![]() .
Пусть область
определения
.
Пусть область
определения
![]() является интервалом, и точка
является интервалом, и точка
![]() .
Составим отношение приращения функции
к приращению аргумента
.
Составим отношение приращения функции
к приращению аргумента
![]() .
Это отношение для конкретной функции
.
Это отношение для конкретной функции
![]() и конкретной точки
и конкретной точки
![]() не
является постоянным; оно зависит от
величины приращения
не
является постоянным; оно зависит от
величины приращения
![]() .
Будем уменьшать приращения аргумента
.
Будем уменьшать приращения аргумента
![]() ,
приближая его к нулю. (Это коротко пишут
так:
,
приближая его к нулю. (Это коротко пишут
так:
![]() .)
Может случиться, что при
.)
Может случиться, что при
![]() отношение приращений
отношение приращений
![]() приближается к какой-то величине
приближается к какой-то величине
![]() .
В этом случае говорят, что в точке
.
В этом случае говорят, что в точке
![]() функция имеет производную
функция имеет производную
![]() ,
и пишут:
,
и пишут:
![]() .
Та функция, которая в точке
.
Та функция, которая в точке
![]() имеет производную, называется
дифференцируемой в точке
имеет производную, называется
дифференцируемой в точке
![]() .
Операция взятия производной называется
дифференцированием функции. Доказывается,
что производная функции обладает
следующими свойствами:
.
Операция взятия производной называется
дифференцированием функции. Доказывается,
что производная функции обладает
следующими свойствами:
-
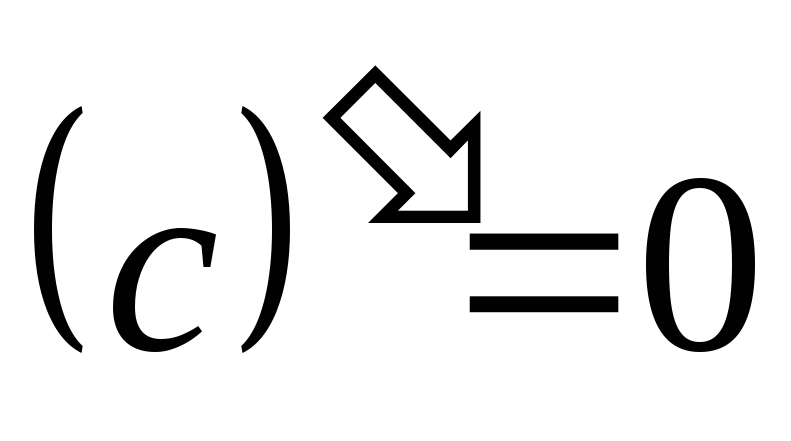 ,
т. е. производная константы равна нулю;
,
т. е. производная константы равна нулю;
-
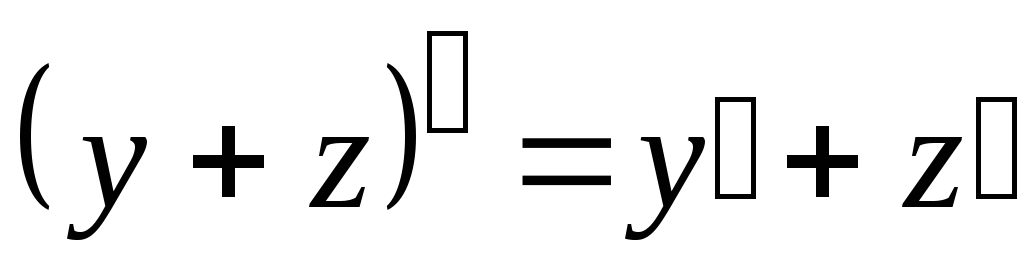 ,
т. е. производная суммы функций равна
сумме их производных;
,
т. е. производная суммы функций равна
сумме их производных;
-
 ,
т. е. производная разности функций
равна разности их производных;
,
т. е. производная разности функций
равна разности их производных;
-
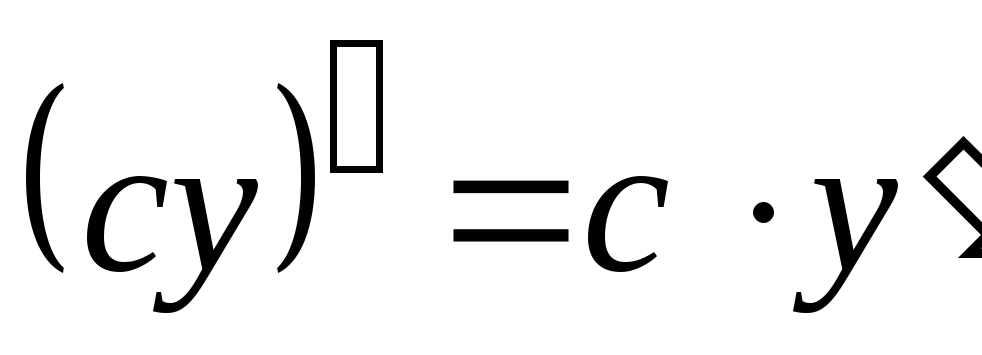 ,
т. е. постоянный множитель можно выносить
за знак производной;
,
т. е. постоянный множитель можно выносить
за знак производной;
-
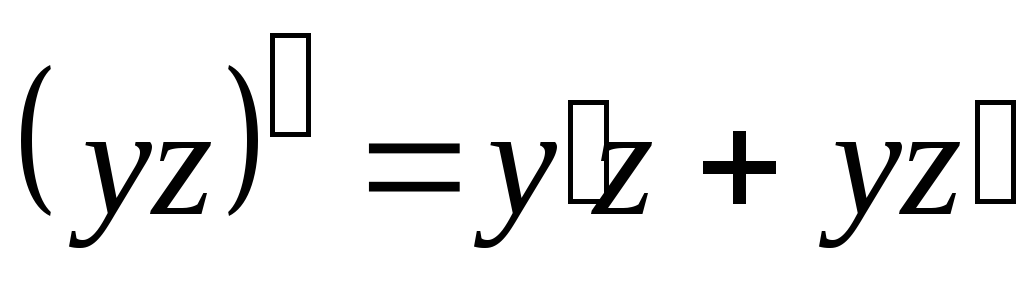 (правило
дифференцирования произведения);
(правило
дифференцирования произведения);
-
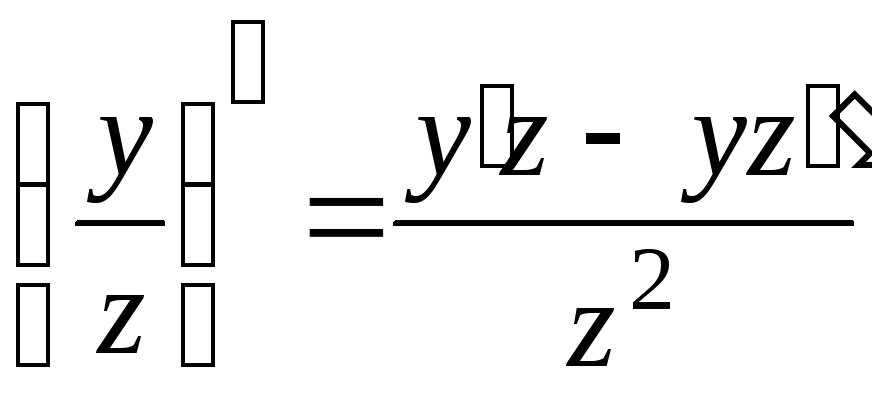 ,
если только
,
если только
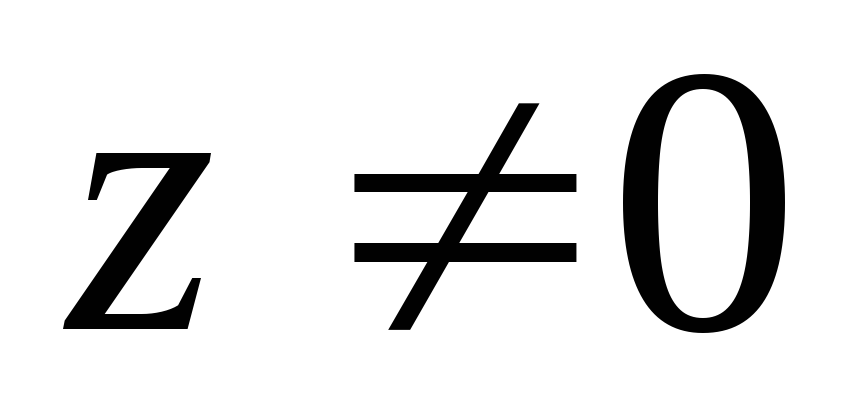 (правило
дифференцирования частного).
(правило
дифференцирования частного).
В школе были доказаны следующие формулы:
-
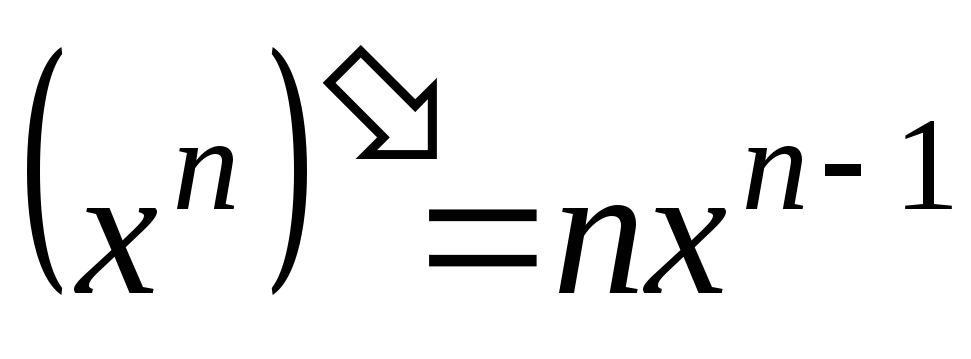 ;
в частности:
;
в частности:
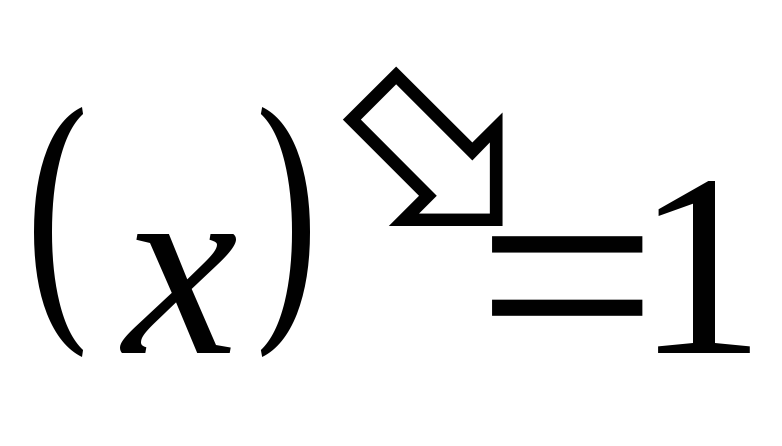 ,
,
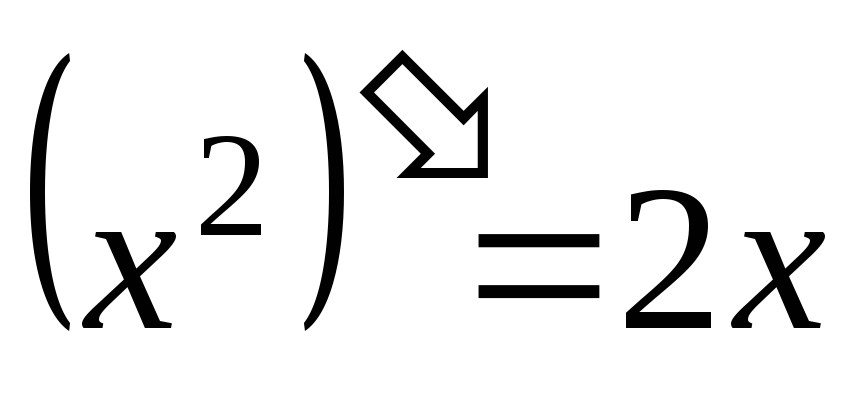 ,
,
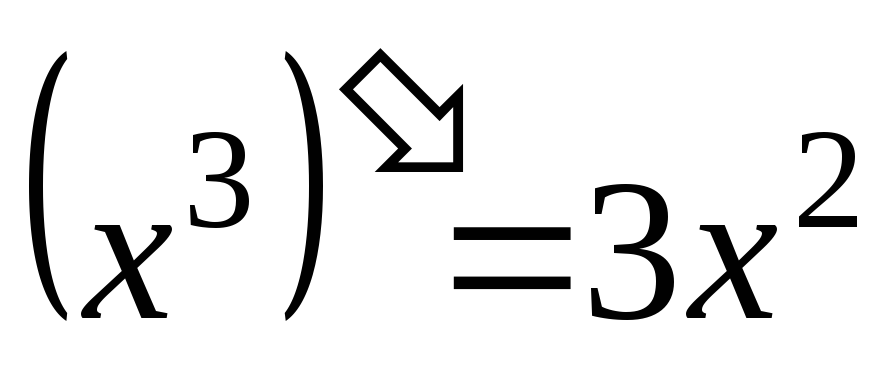 ,
и так далее…;
,
и так далее…;
-
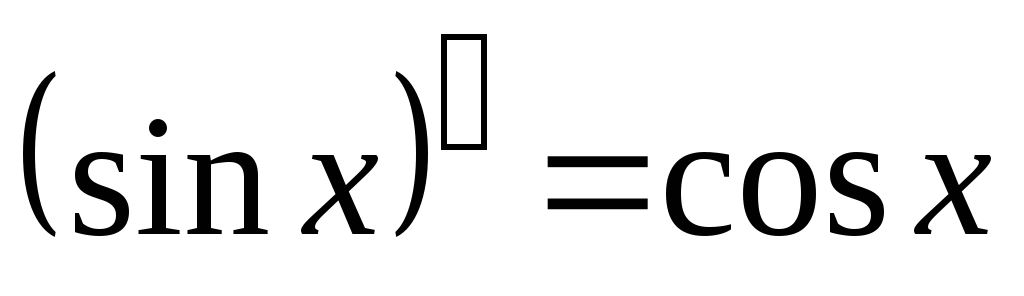 ;
;
-
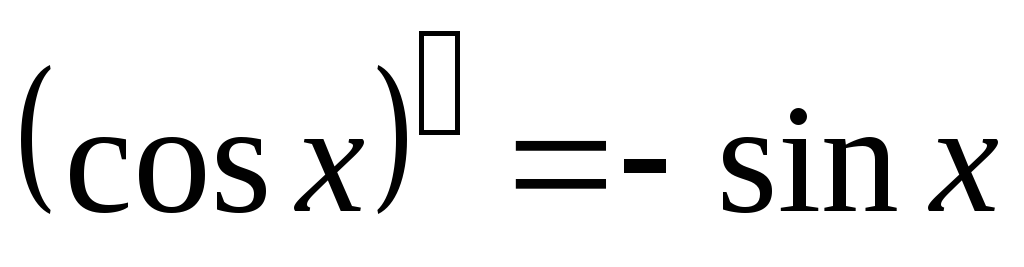 ;
;
-
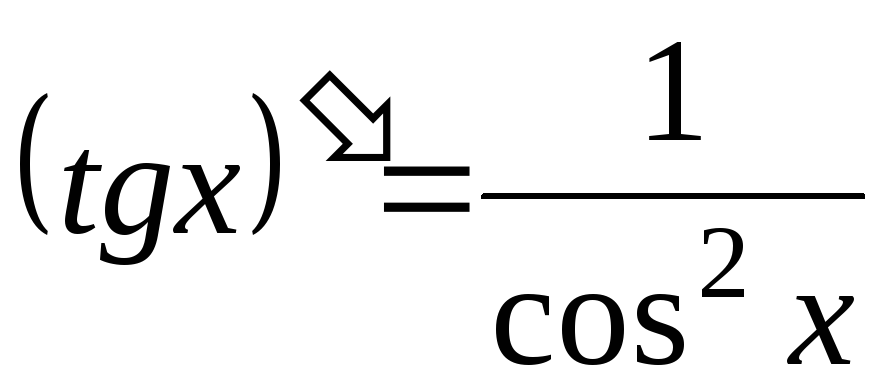 ;
;
-
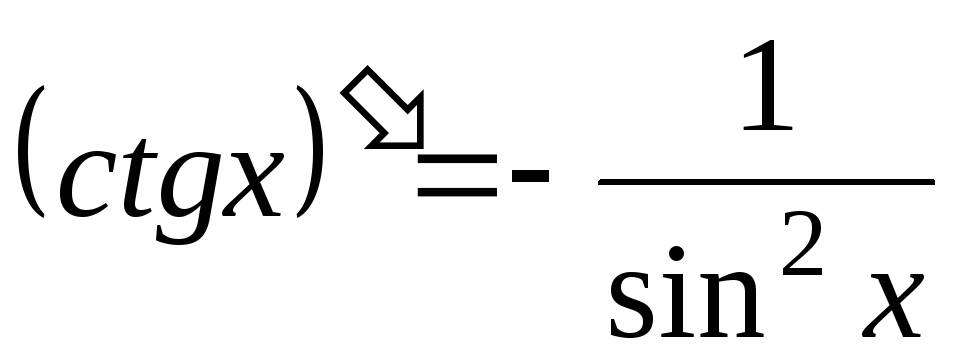 ;
;
-
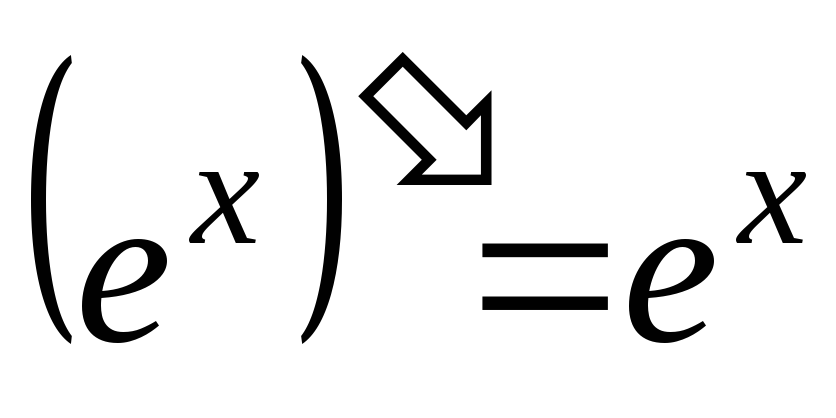 ;
;
-
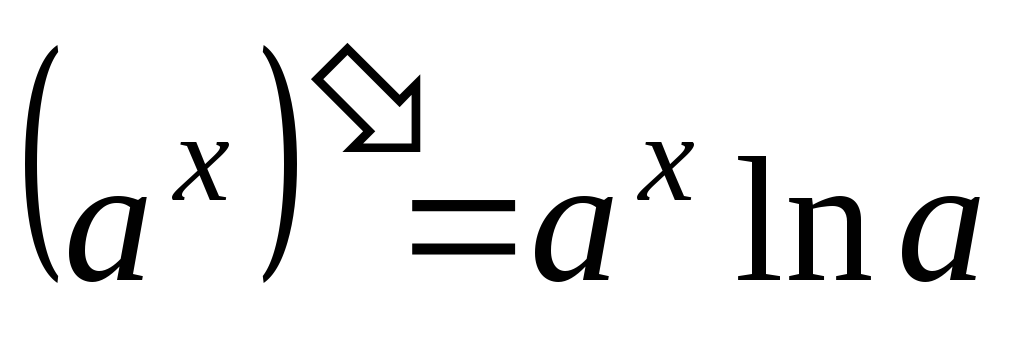 ;
;
-
 ;
;
-
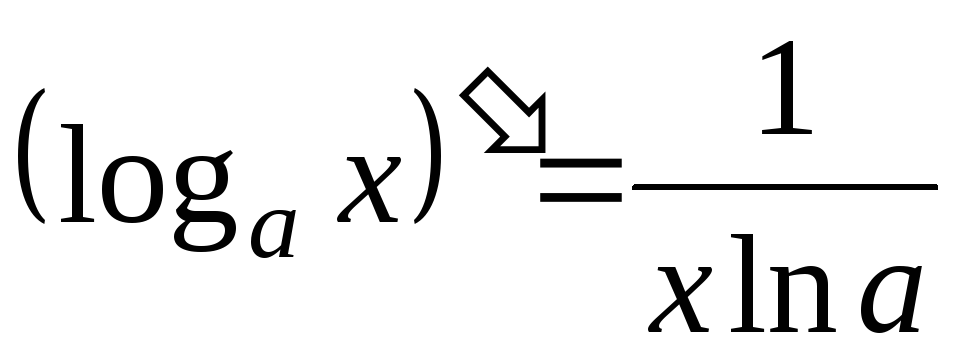 ;
;
-
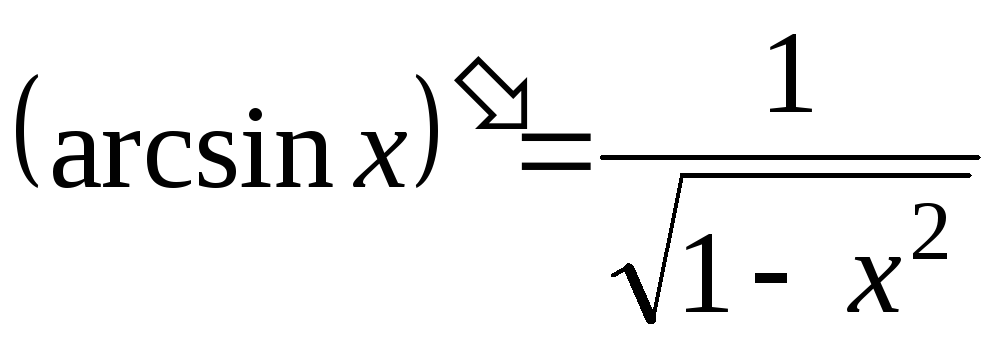 ;
;
-
 ;
;
-
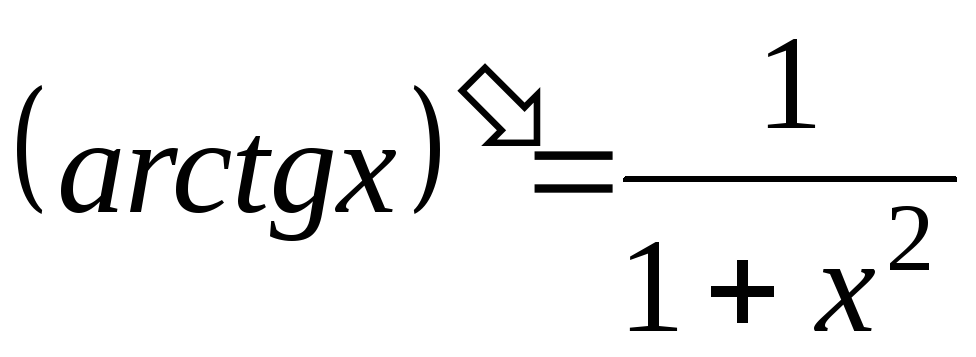 ;
;
-
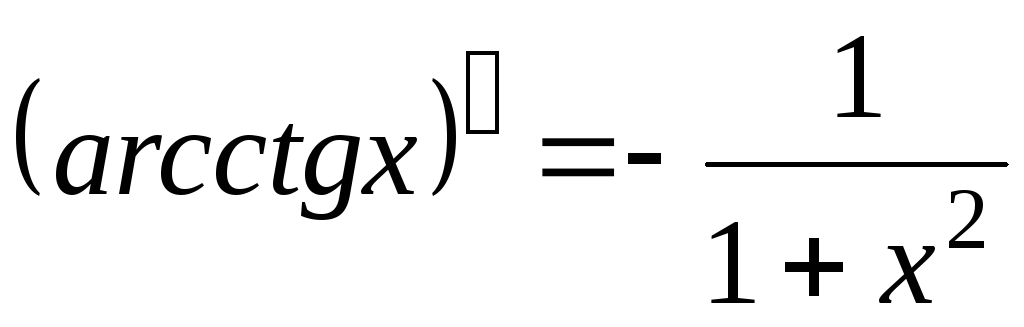 .
.
Правило
дифференцирования сложной функции.
Производная сложной функции равна
производной функции по промежуточному
аргументу, умноженной на производную
промежуточного аргумента по окончательному
аргументу, т. е.
![]() .
.
Замечание. Чтобы найти производную сложной функции, нужно:
-
разбить исходную функцию на элементарные;
-
найти производную от каждой элементарной функции;
-
перемножить все производные.
Первообразная.
В предыдущем параграфе мы по заданной
функции
![]() искали производную
искали производную
![]() .
Теперь попытаемся проделать обратную
операцию. По заданной функции
.
Теперь попытаемся проделать обратную
операцию. По заданной функции
![]() найдем функцию
найдем функцию
![]() такую, что ее производная будет равна
такую, что ее производная будет равна
![]() ,
т. е.
,
т. е.
![]() .
Такая операция называется интегрированием
функции
.
Такая операция называется интегрированием
функции
![]() ,
а сама функция
,
а сама функция
![]() называется
первообраз-ной для функции
называется
первообраз-ной для функции
![]() .
Например, для функции
.
Например, для функции
![]() первообразная равна
первообразная равна
![]() ,
так как
,
так как
![]() .
Для функции
.
Для функции
![]() первообразная равна
первообразная равна
![]() ,
так как
,
так как
![]() .
И так далее… Следует помнить первообразные
для некоторых часто встречающихся
функций.
.
И так далее… Следует помнить первообразные
для некоторых часто встречающихся
функций.
Таблица первообразных.
|
Функция |
Первообразная |
|
Функция |
Первообразная |
|
1.
|
|
|
7.
|
|
|
|
|
|
8.
|
|
|
3.
|
|
|
9.
|
|
|
4.
|
|
|
10.
|
|
|
5.
|
|
|
11.
|
|
|
6.
|
|
|
|
|
Замечание.
Вообще говоря, для функции
![]() первообразную можно найти с точностью
до постоянного слагаемого, потому что
первообразную можно найти с точностью
до постоянного слагаемого, потому что
![]()
![]() .
В таблице для каждой функции указана
одна из первообразных.
.
В таблице для каждой функции указана
одна из первообразных.
Интеграл. Интеграл (точнее, определенный интеграл) находит широкое применение в науке и технике. Для вычисления определенного интеграла используется формула
![]() .
(1)
.
(1)
Формула
(3) называется формулой Ньютона –
Лейбница. В этой формуле
![]() какая-либо первообразная подынтегральной
функции
какая-либо первообразная подынтегральной
функции
![]() .
Формула Ньютона – Лейбница читается
так: «Определенный интеграл равен
разности значений первообразной
подынтегральной функции в верхнем и
нижнем пределах». Определенный интеграл
(2) обладает такими свойствами:
.
Формула Ньютона – Лейбница читается
так: «Определенный интеграл равен
разности значений первообразной
подынтегральной функции в верхнем и
нижнем пределах». Определенный интеграл
(2) обладает такими свойствами:
-
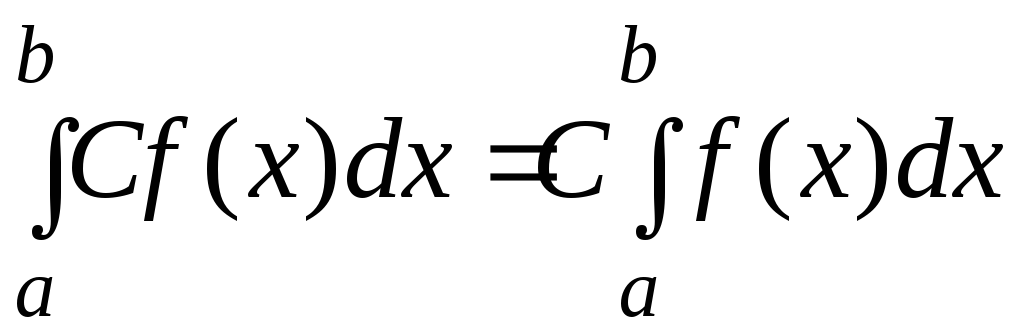 ,
т. е. числовой множитель можно выносить
за знак интеграла;
,
т. е. числовой множитель можно выносить
за знак интеграла;
-
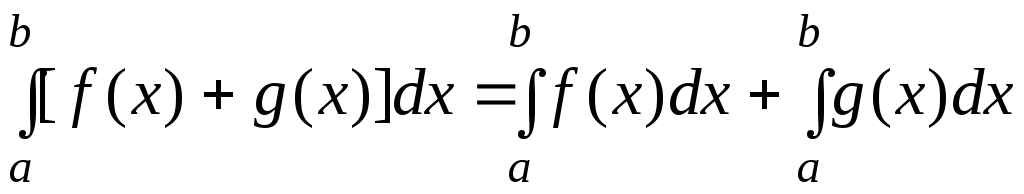 ,
т. е. интеграл от суммы функций равен
сумме их интегралов;
,
т. е. интеграл от суммы функций равен
сумме их интегралов;
-
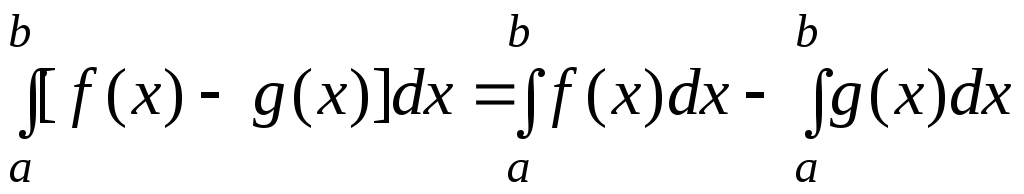 ,
т. е. интеграл от разности функций равен
разности их интегралов;
,
т. е. интеграл от разности функций равен
разности их интегралов;
-
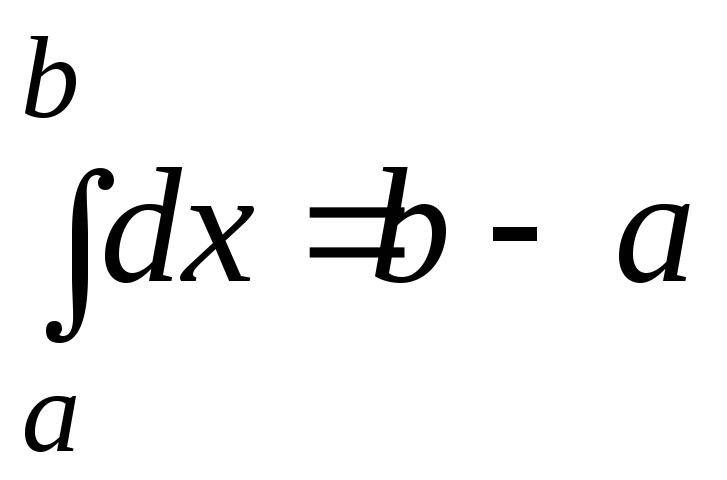 .
.
Геометрический
смысл интеграла. Пусть
подынтегральная функция
![]() неотрицательна на
неотрицательна на
![]() .
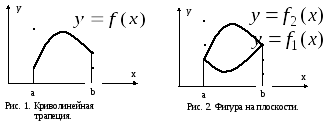
Криволинейной трапецией (см. рис. 1)
называется фигура, ограниченная сверху
графиком функции
.
Криволинейной трапецией (см. рис. 1)
называется фигура, ограниченная сверху
графиком функции
![]() ,
снизу – осью абсцисс, слева и справа –
вертикальными прямыми
,
снизу – осью абсцисс, слева и справа –
вертикальными прямыми
![]() и
и
![]() .
Доказывается, что площадь криволинейной
трапеции находится по формуле
.
Доказывается, что площадь криволинейной
трапеции находится по формуле
![]() (2)
(2)
Таким образом, определенный интеграл от неотрицательной равен площади криволинейной трапеции, ограниченной сверху графиком этой функции. В этом и состоит геометрический смысл определенного интеграла.
С
помощью определенного интеграла можно
находить площади фигур. Итак, пусть
фигура
![]() такова, что ее границу можно разбить на
две части: верхнюю и нижнюю (см. рис. 2).
Пусть
такова, что ее границу можно разбить на
две части: верхнюю и нижнюю (см. рис. 2).
Пусть
![]() уравнение
нижней границы,
уравнение
нижней границы,
![]() уравнение
верней границы. Пусть
уравнение
верней границы. Пусть
![]() проекция
фигуры
проекция
фигуры
![]() на ось абсцисс. Тогда площадь фигуры
на ось абсцисс. Тогда площадь фигуры
![]() находится по формуле
находится по формуле
![]() .
(3)
.
(3)