§ 7. Поле системы осцилляторов, расположенных на плоскости

Предположим, что имеется некоторая плоскость, которую за­полняют осцилляторы, причем все они колеблются в плоскости одновременно, с одной амплитудой и фазой. Чему равно поле на конечном, но достаточно большом расстоянии от плоскости? (Мы не можем выбрать точку наблюдения очень близко от плос­кости, потому что у нас нет точных формул для поля вблизи источников.) Пусть плоскость зарядов совпадает с плоскостью XY и нас интересует поле в точке Р, лежащей на оси z, достаточ­но далеко от плоскости (фиг. 30.10). Предположим, что число зарядов на единичной площадке равно n, а величина каждого заряда д. Все заряды совершают одинаковые гармонические колебания в одном и том же направлении, с той же амплитудой и фазой. Смещение заряда из его среднего положения описы­вается функцией x₀cost. Вводя комплексную амплитуду, действительная часть которой дает реальное движение, будем описывать колебание заряда функцией x₀e^it.

Чтобы найти поле, создаваемое всеми зарядами в точке Р, нужно вычислить сначала поле отдельного заряда q, а затем сложить поля всех зарядов. Как известно, поле излучения про­порционально ускорению заряда, т. е.. — ²x₀е^it (и одинаково для всех зарядов). Электрическое поле в точке Р, создаваемое зарядом в точке Q, пропорционально ускорению заряда q, нужно только помнить, что поле в точке Р в момент времени t определяется ускорением заряда в более ранний момент времени t' =t-r/c, где r/c — время, за которое волна проходит расстояние от Q до Р. Поэтому поле в точке Р пропорционально

(30.10)

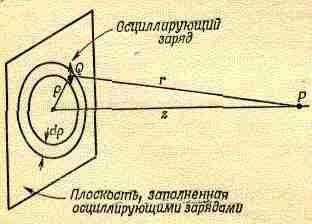
Фиг. 30.10. Поле излучения ос­циллирующих зарядов, заполняю­щих плоскость.

Подставляя это значение ускорения в формулу для поля, соз­даваемого зарядом на большом расстоянии, получаем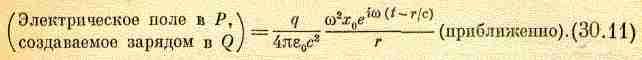

Однако эта формула не совсем правильна, поскольку нужно брать не все ускорение целиком, а его компоненту, перпендику­лярную линии QP. Мы предположим, однако, что точка Р нахо­дится от плоскости намного дальше, чем точка Q от оси z (рас­стояние  на фиг. 30.10), так что для эффектов, которые мы хо­тим учесть, косинус можно заменить единицей (косинус и так довольно близок к единице).

Полное поле в точке Р получается суммированием вкладов от всех зарядов в плоскости. Разумеется, мы должны взять векторную сумму полей. Но поскольку направление поля при­мерно одинаково для всех зарядов, в рамках сделанного прибли­жения достаточно сложить величины всех полей. Кроме того, в нашем приближении поле в точке Р зависит только от r, сле­довательно, все заряды с одинаковым r создают равные поля. Поэтому, прежде всего, сложим поля всех зарядов в кольце ши­риной d и радиусом . Интегрируя затем по всем , получаем полное поле всех зарядов.

Число зарядов в кольце равно произведению площади кольца, 2nd, на  — плотность зарядов на единицу площади. Отсюда

Интеграл берется в пределах =0 и =. Время t, конечно, зафиксировано, так что единственными меняющимися величинами являются  и r. Отвлечемся пока от постоянных множителей, включая и e^it, и вычислим интеграл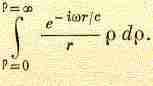

(30.13)

Для этого учтем соотношение между  и r:

(30.14)

При дифференцировании формулы (30.14) z нужно считать независимым от , тогда

2rdr = 2d,

что очень кстати, поскольку при замене в интеграле d на rdr знаменатель r сокращается. Интеграл приобретает более простой вид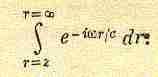

(30.15)

. Экспонента интегрируется очень просто. Нужно поставить в знаменатель коэффициент при r в показателе экспоненты и взять саму экспоненту в точках, соответствующих пределам. Но пределы по r отличаются от пределов по р. Когда =0, нижний предел r=z, т. е. пределы по r равны z и бесконечности. Ин­теграл (30.15) равен

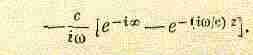
(30.16)

Вместо (r/с) мы здесь написали , поскольку и то и другое означает просто сколь угодно большую величину!

А вот е^-i— величина загадочная. Ее действительная часть, равная cos (-), с математической точки зрения величина со­вершенно неопределенная. [Хотя можно допустить, что она на­ходится где-то [а может быть и всюду (?)—между +1 и -1!]Но в физической ситуации эта величина может означать нечто вполне разумное и обычно оказывается равной нулю. Чтобы убедиться, что это так в нашем случае, вернемся к первоначальному инте­гралу (30.15)

Выражение (30.15) можно понимать как сумму большого числа маленьких комплексных чисел, модуль которых ar, a угол в комплексной плоскости =-r/с. Попробуем оценить эту сумму графически. На фиг. 30.11 отложены первые пять членов суммы. Каждый отрезок кривой имеет длину r и рас­положен под углом  =-(r/с) к предыдущему отрезку. Сум­ма первых пяти слагаемых обозначена стрелкой из начальной точки к концу пятого отрезка. Продолжая прибавлять отрезки, мы опишем многоугольник, вернемся примерно к начальной точке и начнем описывать новый многоугольник. Чем большее число отрезков мы будем прибавлять, тем большее число раз мы обернемся, двигаясь почти по окружности с радиусом с/. Теперь понятно, почему интеграл дает при вычислении неопре­деленный ответ!

Здесь мы должны обратиться к физическому смыслу нашего примера. В любой реальной ситуации плоскость зарядов не может быть бесконечной, а должна где-то оборваться. Если плоскость резко обрывается и ее граница имеет точно форму окружности, то наш интеграл будет равен некоторому значению на этой окружности (см. фиг. 30.11). Если же плотность зарядов

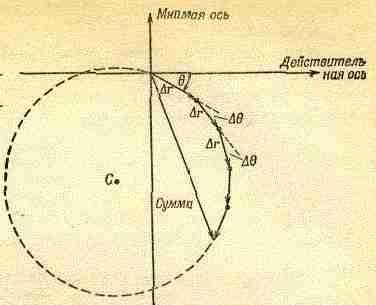
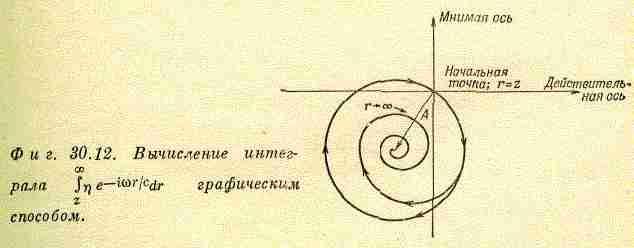
Фиг. 30.11. Вычисление интегра­ла

графическим способом.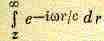

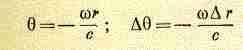
постепенно уменьшается по мере удаления от центра (или обра­щается в нуль вне некоторой границы неправильной формы, так что для достаточно больших  вклад всего кольца шириной d равен нулю), то коэффициент ню в точном интеграле убывает, стремясь к нулю. Поскольку длина добавляемых отрезков в этом случае уменьшается, а угол  остается тем же самым, график кривой, соответствующей интегралу, будет иметь вид спирали. Спираль оканчивается в центре первоначальной ок­ружности, как изображено на фиг. 30.12. Физически правиль­ное значение интеграла дается величиной А, которой на схеме соответствует расстояние от начальной точки до центра окруж­ности, равное как нетрудно убедиться.

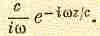
(30.17)

Точно такой же результат мы получили бы из (30.16), положив e^-i=0.

(Есть еще одна причина, почему вклад в интеграл от больших значений r стремится к нулю,— это опущенный нами множитель, учитывающий проекцию ускорения на плоскость, перпендику­лярную линии PQ.)

Нас, конечно, интересует именно случай, имеющий физи­ческий смысл, поэтому мы положим е^-i равным нулю. Возвраща­ясь к формуле (30.12) для поля и вводя все опущенные ранее множители, мы получаем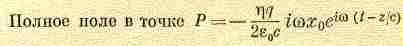

(30.18)

(помня, что l/i =-i).

Интересно отметить, что ix₀e^it в точности равно скорости зарядов, так что выражения для поля можно переписать в виде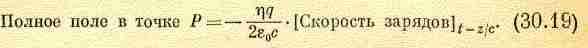

Этот результат немного странен, потому что запаздывание отве­чает расстоянию z, которое есть кратчайшее расстояние от Р до плоскости. Но таков ответ, и, к счастью, формула довольно проста. [Добавим кстати, что, хотя формулы (30.18) и (30.19) бы­ли получены только для достаточно большого расстояния от плоскости, обе они оказываются правильными для любых z,

даже для z<.]

*В нашем случае T=/с=mn,/с, где с — скорость света. Частота v=c/, так что v=c/².

*Прежде всего потому, что сам критерий Рэлея приближенный. Он только указывает область углов, где трудно разобрать, сколько звезд на изображении — одна или две. А в действительности, если точно измерить распределение интенсивности, можно различить два источника при углах , даже меньших /L.