
- •Введение
- •1. Множества и отношения
- •1.1. Понятие множества и антиномии
- •1.2. Аксиомы Цермело-Френкеля
- •1.3. Операции над отношениями
- •1.4. Отношение эквивалентности и фактор-множество
- •1.5. Отношение порядка
- •1.6. Принцип максимальности
- •1.7. Понятие мощности
- •1.8. Антиномия Кантора
- •1.9. Аксиома выбора и сравнения мощностей
- •1.10. Счетные множества
- •1.11. Булевы алгебры
- •2. Булевы функции
- •2.1. Функции и константы алгебры логики
- •2.2. Несущественные переменные и равенство функций
- •2.3. Специальные булевы функции
- •2.4. Реализация функций формулами
- •2.5. Совершенная дизъюнктивная нормальная форма
- •2.6. Минимизация методом карт Карно
- •3. Исчисление высказываний
- •3.1. Исчисление высказываний l
- •3.2. Теорема о дедукции
- •3.3. Интерпретации исчисления высказываний
- •3.4. Аксиомы Клини для исчисления высказываний
- •3.5. Теорема компактности для исчисления высказываний
- •1. Множества и отношения 4
- •2. Булевы функции 15
- •3. Исчисление высказываний 22
3.4. Аксиомы Клини для исчисления высказываний
Обобщим
понятие исчисления L.
Отношением на
множестве X
называется любое подмножество
![]() Xn
= {(x1,…,xn):
xi
Xn
= {(x1,…,xn):
xi
![]() X
при 1
X
при 1
![]() i
i
![]() n}.
n}.
Определение.
Формальная теория Т состоит из четвёрки
множеств (![]() ,
,![]() ,
,![]() ,
,![]() ),
определяемых следующим образом:
),
определяемых следующим образом:
-
 – произвольное
множество, его элементы называются
символами,
а само
– произвольное
множество, его элементы называются
символами,
а само
 – алфавитом;
– алфавитом; -
 – множество слов,
состоящих из символов, элементы из
– множество слов,
состоящих из символов, элементы из
 называются формулами;
называются формулами; -
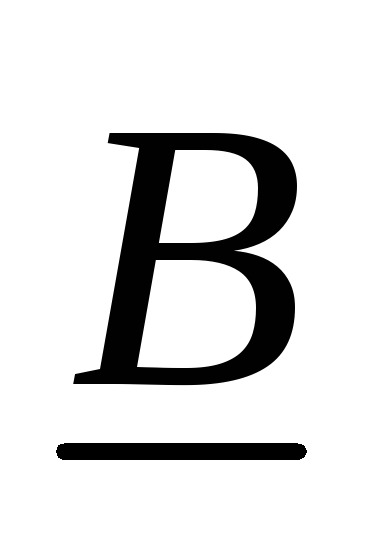 – подмножество
множества всех формул, элементы которого
называются аксиомами;
– подмножество
множества всех формул, элементы которого
называются аксиомами; -
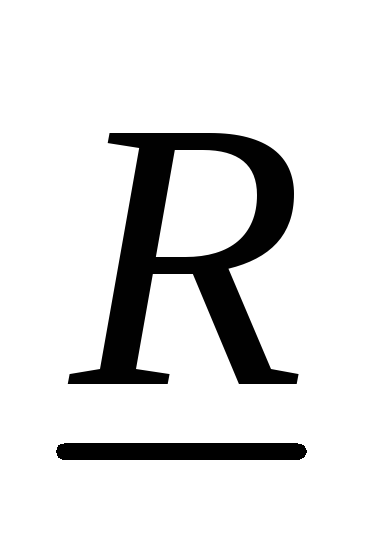 – множество отношений
на множестве формул, элементы из
– множество отношений
на множестве формул, элементы из
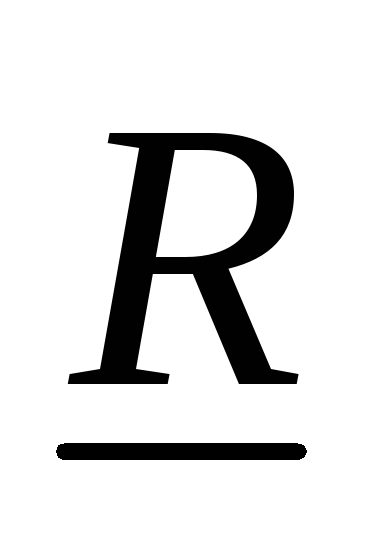 называются правилами вывода.
называются правилами вывода.
Формула
А называется непосредственным
следствием формул
F1,F2,…,Fn,
если (F1,F2,…,Fn,А)
![]() r,
для некоторого r
r,
для некоторого r![]()
![]() .
В этом случае пишут:
.
В этом случае пишут:
![]()
Выводом формулы А из формул, принадлежащих r = {X1,X2,…,Xk} называется последовательность формул:
А1, А2,…,Аn = А,
такая, что,
для каждого 1
![]() i
i
![]() n,
формула Аi
является либо аксиомой, либо Аi
n,
формула Аi
является либо аксиомой, либо Аi
![]() Г, либо Аi
– непосредственное следствие некоторых
формул Аj
Г, либо Аi
– непосредственное следствие некоторых
формул Аj
![]() {A1,
A2,…,Ai-1}.
Если формула А имеет вывод из формул из
Г, то она называется выводимой
из Г, и этот факт
записывается следующим образом:
{A1,
A2,…,Ai-1}.
Если формула А имеет вывод из формул из
Г, то она называется выводимой
из Г, и этот факт
записывается следующим образом:
Г
![]() T
А .
T
А .
В этом случае,
если Г =
, то А называется теоремой
теории Т. Выводимость
Г
![]() T
А, в случае Г
= {X1,X2,…,Xk},
записывается, как
T
А, в случае Г
= {X1,X2,…,Xk},
записывается, как
X1,X2,…,Xk
![]() T
A.
T
A.
Если
А
![]() T
В и В
T
В и В
![]() T
А, то формулы
А и В называются эквивалентными.
T
А, то формулы
А и В называются эквивалентными.
Формальные теории Т1 и Т2 называются равносильными, если существует биекция между классами эквивалентности формул теорий Т1 и Т2, осуществляющая биекцию между теоремами теорий Т1 и Т2.
Исчислением высказываний К называется формальная теория, такая, что
-
множество символов теории К состоит из символов
 ,
,
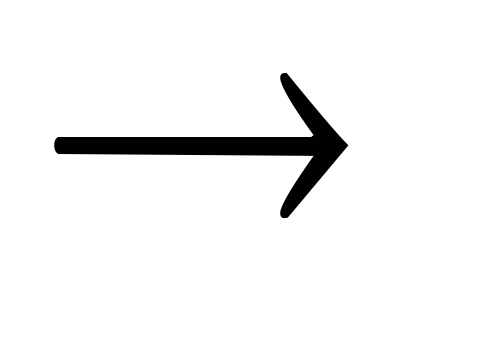 ,
,
 ,
&, ( , ), и элементов произвольного
множества Р,
,
&, ( , ), и элементов произвольного
множества Р, -
множество формул
 теории К определено по индукции: буквы
из Р являются формулами, и для любых А,
В
теории К определено по индукции: буквы
из Р являются формулами, и для любых А,
В

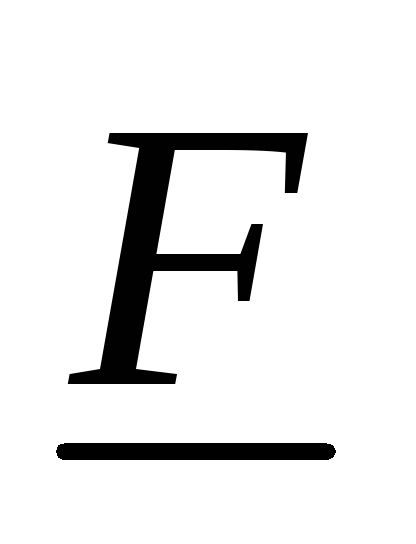 слова
слова
 А,
(А
А,
(А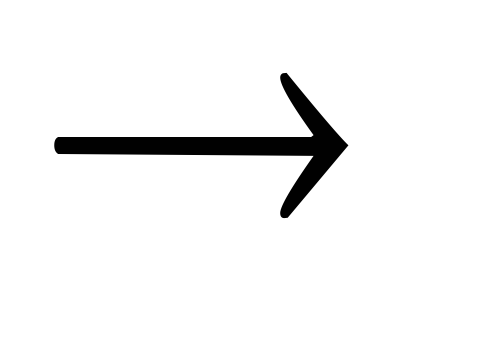 В),
(А
В),
(А В),
(А&В) являются формулами,
В),
(А&В) являются формулами, -
аксиомами теории К служат аксиомы Клини:
(К1)
А![]() (В
(В![]() А),
А),
(К2)
(А![]() (В
(В![]() С))
С))
![]() ((А
((А![]() В)
В)
![]() (А
(А![]() С)),
С)),
(К3)
А&В![]() А,
А,
(К4)
А&В![]() В,
В,
(К5)
А![]() (В
(В![]() (А&В)),
(А&В)),
(К6)
А![]() (А
(А![]() В),
В),
(К7)
В![]() (А
(А![]() В)
В)
(К8)
(А![]() С)
С)
![]() ((В
((В![]() С)
С)
![]() ((А
((А![]() В)
В)
![]() С)),
С)),
(К9)
(А![]() В)
В)
![]() ((А
((А![]()
![]() В)
В)
![]()
![]() А),
А),
(К10)
![]()
![]() А
А![]() А
А
-
правила вывода:
![]() MP
MP
Интерпретацией
теории К называется произвольная функция
e:
![]()
![]() {0,1},
удовлетворяющая для всех А,В
{0,1},
удовлетворяющая для всех А,В![]()
![]() соотношениям:
соотношениям:
e(![]() A)=
A)=![]() ,
e(A
,
e(A![]() B)=e(A)
B)=e(A)
![]() e(B),
e(A&B)=e(A)&e(B), e(A
e(B),
e(A&B)=e(A)&e(B), e(A![]() B)=e(A)
B)=e(A)
![]() e(B).
e(B).
Теорема. Исчисления высказываний К и L равносильны как формальные теории.
Доказательство.
Установим, что каждая формула из К
эквивалентна формуле из L.
Верна теорема А![]()
![]()
![]() А
(см. разд.3.3, упражнение). В силу аксиомы
(К10) это влечёт эквивалентность формул
А и
А
(см. разд.3.3, упражнение). В силу аксиомы
(К10) это влечёт эквивалентность формул
А и
![]()
![]() А.
С помощью аксиомы (К5) и правила вывода
доказывается А,В
А.
С помощью аксиомы (К5) и правила вывода
доказывается А,В
![]() K
А&В. Из аксиом
(К3) и (К4) получаем: А&В
K
А&В. Из аксиом
(К3) и (К4) получаем: А&В
![]() K
А и А&В
K
А и А&В
![]() K
В. В теории L
имеет место тавтология:
K
В. В теории L
имеет место тавтология:
А![]() (В
(В![]()
![]() (А
(А![]()
![]() В)).
В)).
По теореме о полноте существует вывод:
![]() L
А
L
А![]() (В
(В![]()
![]() (А
(А![]()
![]() В)).
В)).
Из теоремы о дедукции следует выводимость:
А,В![]() L
L
![]() (А
(А![]()
![]() В).
В).
Применяя
аксиомы (К3) и (К4), получаем: А&В
![]() K
K
![]() (А
(А![]()
![]() В).
Обратно, из тавтологий
В).
Обратно, из тавтологий
![]() (А
(А![]()
![]() В)
В)
![]() А
и
А
и
![]() (А
(А![]()
![]() В)
В)
![]() В
будем иметь выводы:
В
будем иметь выводы:
![]() (А
(А![]()
![]() В)
В)
![]() L
А и
L
А и
![]() (А
(А![]()
![]() В)
В)
![]() L
В.
L
В.
Следовательно,
формула А&В эквивалентна формуле
![]() (А
(А![]()
![]() В).
Аналогично доказывается эквивалентность
формул А
В).
Аналогично доказывается эквивалентность
формул А![]() В
и
В
и
![]() А
А![]() В.
В.
Рассмотрим
отображение, сопоставляющее каждой
формуле из К формулу из L
с помощью замены связок: А&В на
![]() (А
(А![]()
![]() В),
А
В),
А![]() В
на
В
на
![]() А
А![]() В.
Это преобразование будет переводить
эквивалентные формулы из К в эквивалентные
формулы из L.
Аксиомы (К1) – (К10) превратятся в тавтологии
в теории L.
По теореме о тавтологии они будут
теоремами теории L.
Значит, каждая теорема теории К будет
переходить в теорему теории L.
Поскольку каждая формула теории L
является формулой теории К, то это
преобразование осуществляет биекцию
между классами эквивалентности формул
и между теоремами теорий К и L.
Теорема доказана.
В.
Это преобразование будет переводить
эквивалентные формулы из К в эквивалентные
формулы из L.
Аксиомы (К1) – (К10) превратятся в тавтологии
в теории L.
По теореме о тавтологии они будут
теоремами теории L.
Значит, каждая теорема теории К будет
переходить в теорему теории L.
Поскольку каждая формула теории L
является формулой теории К, то это
преобразование осуществляет биекцию
между классами эквивалентности формул
и между теоремами теорий К и L.
Теорема доказана.
Следствие. Для исчисления высказываний К справедливы теоремы о дедукции и полноте.
