39

4. Теории первого порядка

Модели теории первого порядка определяются как множества с заданными на них операциями и отношениями, удовлетворяющими аксиомам. К таким моделям относятся, например, частично упорядоченные множества и булевы алгебры.

Теории первого порядка возникли с целью формализации и строгого обоснования математики. В 1901 году Дедекинд предложил первое обоснование арифметики, известное теперь под названием системы аксиом Пеано. В 1908 году Цермело сформулировал аксиомы теории множеств. Так было установлено, что множество натуральных чисел и класс всех множеств тоже являются моделями теорий первого порядка. Это стимулировало развитие теории моделей, основные теоремы которой были доказаны Лёвенгеймом (1915 г.), Скулемом (1920 г.), Гёделем (1930 г.), Мальцевым (1936 г.).

Главное внимание в данной главе будет уделено доказательствам теоремы Мальцева о компактности, теорем Гёделя о непротиворечивости исчисления предикатов и о полноте теории первого порядка. Отметим теоремы Лёвенгейма-Скулема, из которых следует существование счётной модели теории множеств и несчётной модели теории натуральных чисел. Рассмотрим метод резолюций Робинсона (1965 г.) автоматического доказательства предложений исчисления предикатов.

4.1. Термы и предикаты

Термы и их унификация

Упрощённо можно сказать, что термы – это алгебраические выражения, определяющие функции, значения которых вычисляются с помощью операций. Например, в булевой алгебре А определены операции: , , , и из этих операций можно составлять термы, например, , , . Перейдём к точным определениям.

Пусть – счётное множество, элементы которого будут называться переменными, F – произвольное множество, элементы которого будут называться функциональными символами, – произвольная функция. Элементы f  F, для которых , называются n-арными операциями. Например, для булевой алгебры множество функциональных символов будет равно: F = {, , }, значения функции # равны #() = 2, #() = 2, #() = 1, поэтому все элементы из F – операции. Символы c  F, для которых #(с) = 0, называются символами констант. Термы определим по индукции:

1. переменные и символы констант являются термами;

2. если 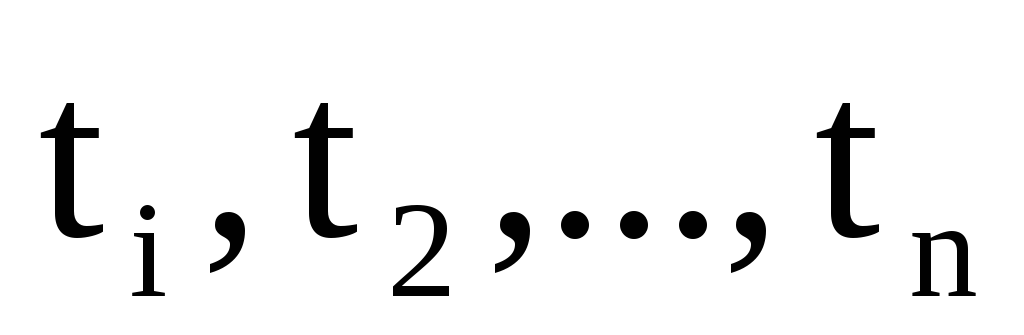– термы и f – n-арная операция, то – терм;

3. кроме построенных с помощью правил 1 – 2, других термов нет.

В определении терма участвует префиксная форма операции. Заметим, что бинарные операции записываются обычно в инфиксной форме. Например, вместо применяется запись: . Учитывая приоритеты операций, скобки часто опускают, в частности, приведённая запись равносильна выражению: , ибо приоритет операции  выше приоритета .

Согласно определению терма, множество всех термов T(F) содержит множество переменных X. Подстановкой называется отображение такое, что для всех x  X, за исключением элементов некоторого конечного подмножества из X, имеет место v(x) = x. Распространим подстановку v до некоторой функции , полагая

1. если t  X, то v(t) = v(t);

2. если t – символ константы, то v(t) = t;

3. если для некоторой n-арной операции f и термов , то .

Терм v(t) называется результатом применения подстановки v к терму t. Например, результатом подстановки

, ,

в терм будет терм: . Если значения не указаны, то по умолчанию . Подстановку записывают как множество пар , например: .

Пусть заданы два терма s и t, и пусть надо найти подстановку, делающую эти термы равными. Эта задача решается следующим образом.

Подстановка v называется унификатором термов s и t, если v (s) = v (t). Унификатор v называется наибольшим общим унификатором термов s и t и обозначается: m.g.u.(s, t) = v, если для любого другого унификатора w термов s и t существует такая подстановка , что  _ v = w. Если для термов s и t существует хотя бы один унификатор, то среди унификаторов существует наибольший общий. Для его нахождения предлагается следующий алгоритм.

Алгоритм унификации термов с использованием стека

Вход: термы s, t.

Выход: подстановка , записанная как список пар , если t и s обладают наибольшим общим унификатором. Процедура возвращает отказ, если унификаторов нет.

Действия:  = ; запомнить пару (s = t) в стек;

Пока стек не пуст, выполнять цикл:

Тело цикла: Извлечь из стека пару термов ( = ) и произвести одно из следующих действий, в зависимости от выполнения одного из условий

1. если  – переменная,  – терм, не содержащий вхождений , то все вхождения переменной  в стеке заменяются на  и все вхождения  в  заменяются на , затем подстановка  =  добавляется к списку подстановок в ;

2. если  – переменная, а  – терм, то произвести действия, как в I, поменяв ролями  и  (к  добавляется пара  = );

3. если  и  – составные термы, 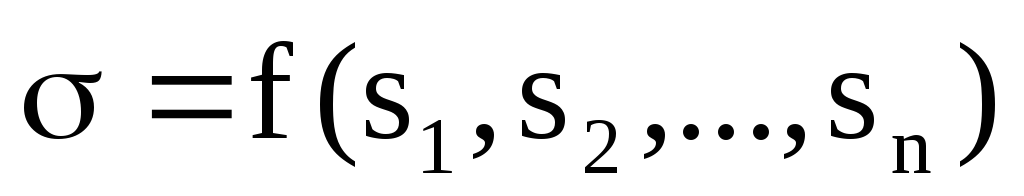и , то все пары , 1  i  n, запоминаются в стек;

4. если  и  – одинаковые символы констант или переменных, то ничего не делать;

5. во всех остальных случаях производится выход из цикла и возвращается отказ.

Конец тела цикла.

Если выход из цикла произошёл не после выполнения условия V, то  содержит элементы искомой подстановки.

Пример

s = (a  b)  ((a  b)  d), t = (a  b)  (c  (a  b)).

1. Устанавливаем  = ; запоминаем в стек пару (s = t);

2. извлекаем (s = t) из стека, имеет место случай III, запоминаем в стек пары и ((a  b)  d = c  (a  b));

3. извлекаем из стека ((a  b)  d = c  (a  b)), имеет место случай III, запоминаем в стек (a  b = c) и (d = a  b);

4. извлекаем из стека (d = a  b), имеет место случай I,  = {(d = a  b)};

5. извлекаем из стека (a  b = c), имеет место случай II, ;

6. извлекаем из стека , изменений в  нет;

7. стек пуст, возвращаем .

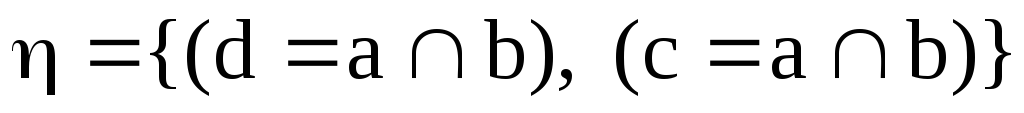Система уравнений

Пусть задано несколько пар термов и необходимо найти подстановку w, которая превращает все пары термов в равные . Эта задача называется системой уравнений: .

Унификатором системы уравнений называется подстановка v, которая является унификатором пар для всех 1  i  n. Система уравнений , 1  i  n, называется находящейся в разрешённой форме, если каждое из этих уравнений имеет вид: для некоторого элемента , причём переменная не входит в терм ни при каком i. Такая система имеет унификатором подстановку: , которая будет наиболее общим унификатором этой системы. Редукцией термов называется замена уравнения системой уравнений: .

Недетерминированный алгоритм решения множества уравнений

Вход: множество уравнений .

Выход: множество уравнений в разрешённой форме .

Действия: пока истинно условие применимости хотя бы одного из перечисленных далее преобразований, выполнять в цикле альтернативы.

Начало цикла:

1. если существует уравнение вида: t = x, где t – не переменная, а x – переменная, то заменить это уравнение на x = t; в противном случае

2. если существует уравнение вида: x = x, где x – переменная, то удалить это уравнение из системы уравнений; в противном случае

3. если существует уравнение вида: s = t, в котором s и t не являются переменными, то если корневые функции термов s и t различны, тогда возвращается «отказ», в противном случае осуществить преобразование редукции термов;

4. если существует уравнение вида: x = t, такое, что переменная x не входит в другие уравнения системы и терм t отличен от x, то если переменная x входит в t, тогда возвращается «отказ», в противном случае осуществить преобразование элиминации переменной.

Конец цикла. (Возвращается «успех», преобразованная система уравнений будет искомым унификатором.)

Здесь под элиминацией переменной понимается переход от системы уравнений к системе, полученной после подстановки x = t.

Пример

Рассмотрим систему, состоящую из одного уравнения:

((a  b)  d)  (a  b) = (c  (a  b)  (a  b)}

1) Применяем случай III, делаем редукцию, получаем:  = {(a  b)  d) = c  (a  b), a  b = a  b}.

2) Применяем случай III, получаем:  = {a  b = с, d = a  b, a  b = a  b}.

3) Применяем случай III для последнего уравнения и повторяем 2 раза случай II, это приводит к  = {a  b = с, d = a  b}.

4) Применяем случай I, получаем ответ:  = {c = a  b, d = a  b}.

Предикаты и отношения

Функция n переменных, принимающая значения 0 и 1, называется n-местным предикатом. Каждому отношению соответствует предикат, равный характеристической функции подмножества R. Ясно, что определение n-местного предиката на множестве А равносильно заданию отношения:

Пусть и – предикаты. Конъюнкцией P и Q называется предикат , дизъюнкцией – предикат , отрицание определяется с помощью предиката .

Для предикатов определяются кванторы существования и всеобщности. Пусть – n-местный предикат. Запись: означает, что существует , для которого =1, запись: означает, что =1 для всех . Аналогично определяются предикаты и , при . В этих случая говорят, что переменная связана квантором. Предикаты и будут зависеть от n-1 переменных. В случае, когда , положим и . Тем самым мы определим предикаты и для любых символов переменных x. Отношение, соответствующее предикату будет проекцией отношения, определяемого P, на область , оно будет равно объединению по всем A отношений, определяемых предикатами . Предикату соответствует отношение, равное пересечению этих отношений. Таким образом,

;

.