
- •4. Теории первого порядка
- •4.1. Термы и предикаты
- •4.2. Язык логики предикатов
- •Аксиомы кванторов
- •Аксиомы равенства
- •4.3. Семантика языка логики предикатов
- •4.4. Модели теории первого порядка
- •4.5. Компактность и полнота языка первого порядка
- •4.6. Упрощение формул
- •4.7. Метод резолюций Робинсона
- •5. Нечеткая логика
- •5.1. Нечеткие множества
- •5.2. Логические операции
- •X (a b), если и только если X a b.
- •5.3. Нечеткие отношения
- •5.4. Пропозициональная нечёткая логика
- •5.5. Вывод с нечёткими посылками
- •4. Теории первого порядка 26
- •5. Нечеткая логика 42
4.4. Модели теории первого порядка
Среди моделей языка первого порядка выделяются модели, удовлетворяющие набору аксиом. Этот набор и будет определять теорию, а модели, для которых выполнены аксиомы, будут моделями теории.
Теорией (первого порядка) Т в языке L называется произвольное множество предложений языка L.
Таким образом, теория получается из исчисления предикатов добавлением некоторого множества предложений T.
Моделью
теории Т называется модель А языка
L, такая, что A |= для
всех
Т. Теория Т непротиворечива,
если она состоит из непротиворечивого
множества предложений. Если существует
модель теории Т, то Т называется
выполнимой. Множеством аксиом
теории Т называется всякое её
подмножество
Т такое, что для каждого предложения
Т существует вывод
![]() .
Если существует конечное множество
аксиом, то Т называется конечно
аксиоматизируемой.
.
Если существует конечное множество
аксиом, то Т называется конечно
аксиоматизируемой.
Рассмотрим теории наиболее часто встречающихся моделей.
Теория частично упорядоченных множеств
Язык L = {} состоит из одного двухместного предиката. Теория имеет 3 аксиомы:
1) xyz (x y & y z x z);
2) xy (x y & y x x = y);
3) x (x x);
Моделями этой теории являются частично упорядоченные множества. Если присоединить аксиому:
4) xy (x y y x),
то получим теорию, моделями которой служат линейно упорядоченные множества.
Теория булевых алгебр
Язык L = {, , } состоит из символов двух бинарных операций и одной унарной. Теория имеет аксиомы 1 – 6 (разд. 1.11) (все свободные переменные в этих аксиомах превращены в связанные с помощью кванторов всеобщности). Моделями будут булевы алгебры.
Теория групп
Пусть
![]() состоит из символов бинарной и унарной
операций и константы. Теория групп
определяется аксиомами:
состоит из символов бинарной и унарной
операций и константы. Теория групп
определяется аксиомами:
1) xyz (x (y z) = (x y) z);
2) x (e x = x & x e = x);
3)
![]() .
.
Моделями служат группы. Если добавить аксиому коммутативности:
4) xy (x y = y x),
то получим теорию, моделями которой являются абелевы группы.
Теория чисел
Пусть L = {+, , S, 0} состоит из двух бинарных операций + и , унарной операции S и символа константы 0. Теория чисел задаётся аксиомами Пеано:
-
x ((0 = Sx));
-
xy(Sx = Sy x = y);
-
x + 0 = x;
-
x + Sy = S(x + y);
-
x 0 = 0;
-
x Sy = (x y) + x;
-
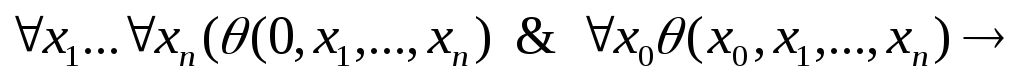
 для каждой формулы ,
не содержащей связанных вхождений
для каждой формулы ,
не содержащей связанных вхождений
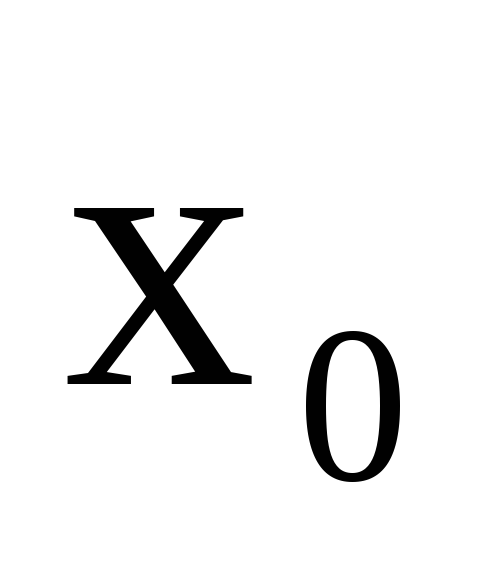 .
.
Аксиома 7 (аксиома индукции) состоит в действительности из бесконечного числа предложений, каждое из которых соответствует некоторой формуле языка L.
Стандартной моделью теории чисел является модель (, +, , S, 0) с обычными операциями сложения и умножения чисел. Операция S интерпретируется как функция S(x) = x + 1. Существуют и нестандартные модели теории чисел.
Теория множеств
Пусть L = {}. Добавим логическую связку , служащую сокращением для ( ) & ( ). Запишем в виде формул аксиомы Цермело-Френкеля(разд. 1.2). Эти аксиомы определяют теорию ZF:
-
xy ((y x)) (пустое множество);
-
xyz ((z x z y) (x = y)) (экстенсиональность);
-
uvxz (z x z = u z = v) (пара);
-
xyzu (u z & z x u y) (объединение);
-
xyu (v(v u v x) u y) (множество подмножеств);
-
x (y (y x) & y (y x z (y z & z x))) (бесконечность);
-
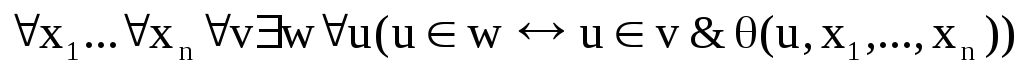 (схема аксиом выделения);
(схема аксиом выделения); -
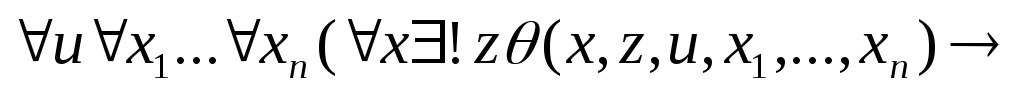
 (схема аксиом подстановки);
(схема аксиом подстановки); -
ux (x u & v((v x & v u))) (регулярность).
Если добавить к этой системе аксиом аксиому выбора, то получится теория ZFC. Существуют различные модели теории множеств. Далее мы увидим, что существуют модели, в которых число всех множеств счётно.
