2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения.

1. При движении тела относительно выбранной системы координат его положение изменяется с течением времени. Движение материальной точки будет полностью определено, если заданы непрерывные и однозначные функции времени t:

x = x(t), y = y(t), z = z(t).

Эти уравнения описывают изменение координат точки от времени и называются кинематическими уравнениями движения.

2. Путь - часть траектории, пройденной телом за определенный промежуток времени. Момент времени t₀, от которого начинается его отсчет, называется начальным моментом времени, обычно t₀=0 в силу произвольного выбора начала отсчета времени.

Длиной пути называется сумма длин всех участков траектории. Длина пути не может быть величиной отрицательной, она всегда положительна. Например, материальная точка переместилась из точки траектории С сначала в точку А, а затем в точку В (Рисунок 1). Длина ее пути равна сумме длин дуги СА и дуги АВ.

2.1.3. Кинематические характеристики. Скорость.

1. Для характеристики быстроты движения тел в физике вводится понятие скорости. Скорость - вектор, а значит, характеризуется величиной, направлением, точкой приложения.

Рассмотрим движение вдоль оси Х. Положение точки будет определяться изменением со временем координаты Х.

Если за время ∆t произошло перемещение точки на ∆r, то величина является средней скоростью движения: .

Средней скоростью движущегося тела называется вектор, равный отношению вектора перемещения к величине промежутка времени, за которое это перемещение произошло.

Модуль средней скорости есть физическая величина, численно равная изменению пути за единицу времени.

2. Для определения скорости в данный момент времени, мгновенной скорости, нужно рассмотреть интервал времени ∆t→0, тогда

.

Используя понятие производной, можно записать для скорости

Скорость тела в данный момент времени называется мгновенной скоростью (или просто скоростью).

Вектор V мгновенной скорости направлен по касательной к траектории в сторону движения тела.

2.1.4. Кинематические характеристики. Ускорение.

1. Быстрота изменения вектора скорости характеризуется величиной, называемой ускорением. Ускорение может возникнуть как за счет изменения величины скорости, так и за счет изменения направления скорости.

Пусть в момент времени t скорость тела равна v₁, а через промежуток времени ∆t в момент времени t + ∆t равна v₂, приращение вектора скорости за ∆t равно ∆v.

Средним ускорением тела в интервале времени от t до t + ∆t называется вектор а_ср, равный отношению приращения вектора скорости ∆v к промежутку времени ∆t:

Cреднее ускорение есть физическая величина, численно равная изменению скорости за единицу времени.

2.Для определения ускорения в данный момент времени, т.е. мгновенного ускорения, нужно рассмотреть малый интервал времени ∆t→0. Тогда вектор мгновенного ускорения равен пределу вектора среднего ускорения при стремлении промежутка времени ∆t к нулю:

Используя понятие производной, можно дать для ускорения следующее определение:

Ускорением (или мгновенным ускорением) тела называется векторная величина а, равная первой производной по времени от скорости тела v или второй производной по времени от пути.

3. При вращении точки по окружности ее скорость может изменяться по величине и по направлению (рисунок 2)

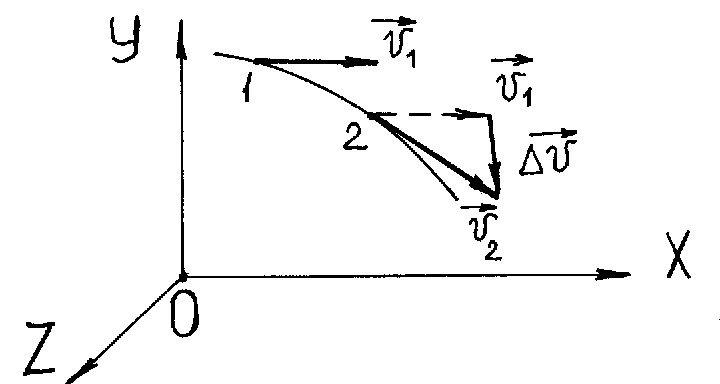
Рисунок 2.- Изменение скорости точки при вращении по

окружности

На рисунке 2 в положении 1 скорость точки v_1, в положении 2 скорость точки v₂. Модуль скорости v₂ больше модуля скорости v₁, ∆v- вектор изменения скорости ∆v = v₂ -v₁

Вращающаяся точка имеет тангенциальное ускорение, равное а _τ=dv/dt, оно изменяет скорость по величине и направлено по касательной к траектории; и нормальное ускорение, равное а _n= v²/R, оно меняет направление скорости и направлено по радиусу окружности (R) (см. Pисунок 3)

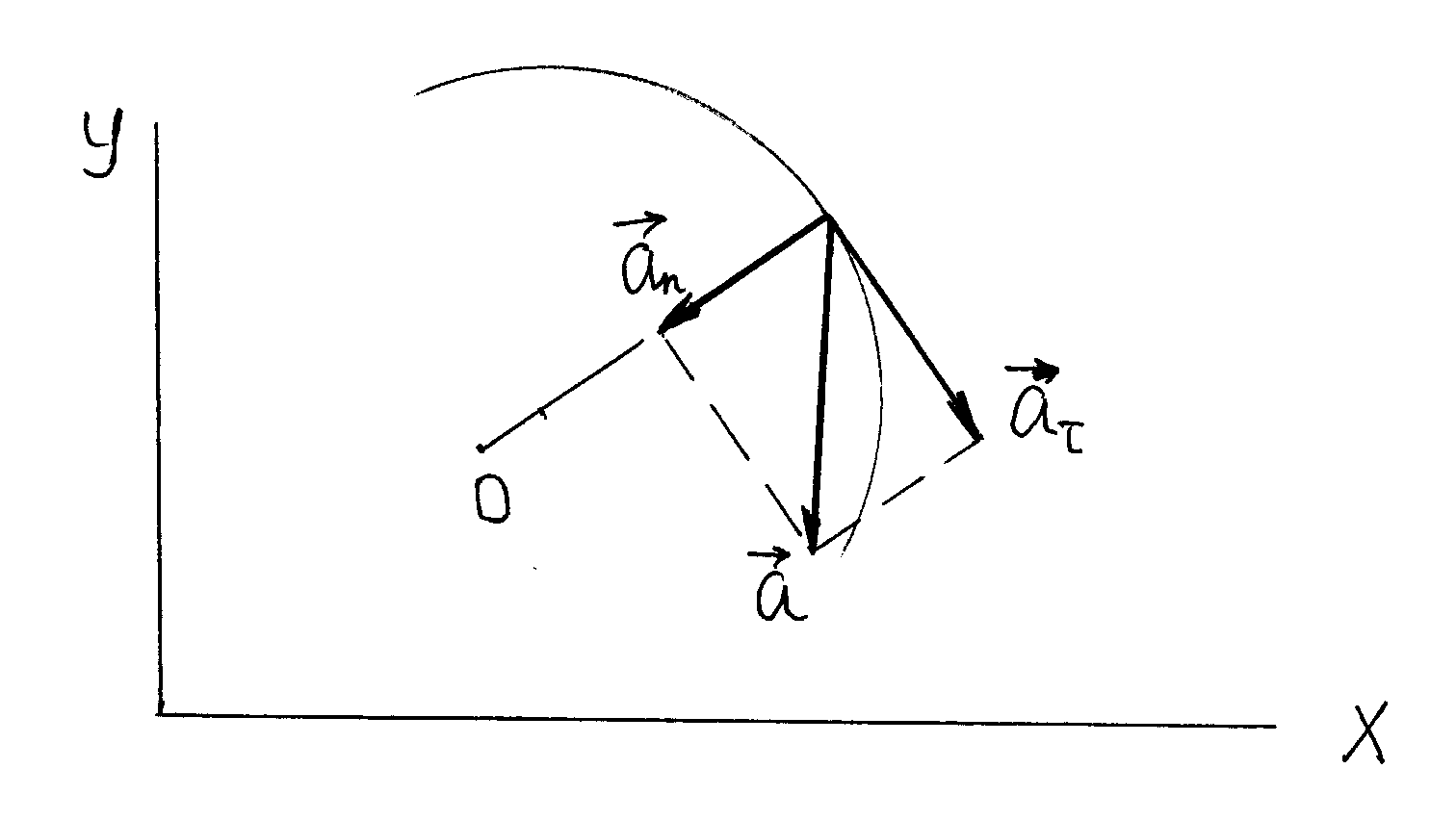
Рисунок 3.- Полное, тангенциальное и нормальное ускорения вращающейся точки

Вектор полного ускорения равен , т.е. он может быть представлен как сумма векторов тангенциального a_τ и нормального a_n ускорений. Модуль полного ускорения равен:

.