4.1.2. Свойства функции распределения многомерной случайной величины.

1. , так как вероятность.

2. есть неубывающая функция по каждому аргументу, т.е. (см. рис.)

,если ;

, если .

3. Имеют место предельные соотно- шения:

при любых значениях остальных аргументов. Действительно, событие – невозможное, поэтому его совмещение с другими любыми событиями также будет невозможным событием.

Свойство вытекает из определения, так как события

достоверны.

4. а) При 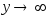функция распределения системы становится функцией распределения составляющей Х:

.

б) Аналогично, при , .

§4.2. Плотность распределения вероятностей двумерной случайной величины.

Как и в одномерном случае непрерывную двумерную величину можно задать, пользуясь плотностью распределения, если функция распределения всюду непрерывна и имеет всюду ( за исключением, может быть, конечного числа точек) непрерывную смешанную частную производную второго порядка.

Плотностью распределения двумерной непрерывной случайной величины называют вторую смешанную производную от функции распределения, т.е.

.

Свойства плотности распределения:

1. как производная от неубывающей функции .

2. .

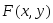§4.3. Условные законы распределения составляющих системы

непрерывных величин.

Пусть – непрерывная двумерная случайная величина. Условной плотностью распределения составляющей Х при данном значении называют отношение плотности распределения к плотности распределения составляющей Y :

,

Аналогично определяется условная плотность распределения составляющей Y при данном значении :

.

Запишем формулы в другом виде:

,

.

Плотность распределения системы случайных величин можно найти, умножив плотность распределения одной из составляющих на условную плотность другой составляющей (см. умножение вероятностей).

§4.4. Условное математическое ожидание двумерной величины.

Условным математическим ожиданием дискретной случайной величины Х при (y определенное возможное значение Y) называют произведение возможных значений Х на их условные вероятности:

.

Для непрерывных случайных величин

.

Аналогично определяется условное математическое ожидание случайной величины Y.

§4.5. Независимые и зависимые случайные величины.

Введем очень важное понятие независимости случайных величин. Это понятие не менее важно, чем понятие независимости событий, и тесно с ним связано. Говоря описательно, случайные величины Х и Y независимы, если независимы любые два события, которые выражаются по отдельности через X и Y.

Для случайных величин, принимающих вещественные значения, дадим следующее определение.

Определение. Случайные величины X и Y независимы, если

, для любых событий и , где числа могут быть произвольными.

Нам незачем стремиться к большей математической аккуратности в определении независимых случайных величин, поскольку им редко пользуются на практике. Дело в том, что независимость случайных величин обеспечивается скорее схемой постановки испытаний, нежели проверкой математических соотношений.