
- •Тема 4. Система случайных величин (многомерные случайные величины).
- •§4.1. Многомерная случайная величина и ее функция распределения
- •4.1.1. Дискретная двумерная случайная величина.
- •4.1.2. Свойства функции распределения многомерной случайной величины.
- •§4.2. Плотность распределения вероятностей двумерной случайной величины.
- •§4.3. Условные законы распределения составляющих системы
- •§4.4. Условное математическое ожидание двумерной величины.
- •§4.5. Независимые и зависимые случайные величины.
- •4.5.1. Ковариация и коэффициент корреляции.
- •§4.6. Вопросы для самопроверки.
- •§4.7. Задачи
- •Тема 5. Предельные теоремы.
- •§5.1. Закон больших чисел.
- •5.1.1. Неравенство Чебышева.
- •5.1.2 Сходимость по вероятности.
- •5.1.3. Закон больших чисел в форме Чебышева.
- •5.1.4. Закон больших чисел в форме Бернулли.
- •§5.2. Центральная предельная теорема.
- •§5.3. Вероятность отклонения относительной частоты от постоянной
- •§5.4. Вопросы для самопроверки.
- •§5.5. Задачи.
Тема 4. Система случайных величин (многомерные случайные величины).
§4.1. Многомерная случайная величина и ее функция распределения
вероятностей.
На одном и том же пространстве элементарных событий может быть определена не одна, а несколько случайных величин. Так, при вероятностном моделировании структуры расходов затраты случайно выбранной семьи на питание, обувь, одежду, транспорт, на удовлетворение духовных потребностей являются случайными величинами, определенными на одном пространстве элементарных событий.
Пусть
![]() – случайные величины, определенные на
множестве элементарных событий
– случайные величины, определенные на
множестве элементарных событий
![]() .
Удобно рассматривать их как координаты
n
– мерного
случайного вектора
.
Удобно рассматривать их как координаты
n
– мерного
случайного вектора
![]() .
Под n
– мерной
случайной величиной, или случайным
вектором, понимается упорядоченный
набор n
случайных
величин
.
Под n
– мерной
случайной величиной, или случайным
вектором, понимается упорядоченный
набор n
случайных
величин
![]() .
.
Для описания
закона распределения многомерной
случайной величины используется функция
распределения случайного вектора
![]() которая есть функция
которая есть функция
![]() векторного аргумента
векторного аргумента
![]() ,
равная вероятности одновременного
выполнения n
неравенств,
т.е.
,
равная вероятности одновременного
выполнения n
неравенств,
т.е.
![]()
В {
} скобках
находится произведение
![]() событий
событий
![]() ,
которые в общем случае могут быть
зависимыми, и поэтому вероятность их
произведения не может быть выражена
через произведения вероятностей этих
событий.
,
которые в общем случае могут быть
зависимыми, и поэтому вероятность их
произведения не может быть выражена
через произведения вероятностей этих
событий.
Ограничимся в
дальнейшем рассмотрением двумерной
случайной величины
![]() ,
которая геометрически может
интерпретироваться как случайная точка
(
,
которая геометрически может
интерпретироваться как случайная точка
(![]() в плоскости
в плоскости
![]()
Из определения получаем
![]()
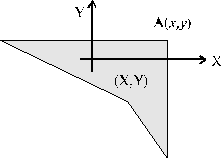
![]() – это вероятность попадания точки (
– это вероятность попадания точки (![]() в заштрихованную область, лежащую левее
и ниже точки
в заштрихованную область, лежащую левее
и ниже точки
![]()
(см. рис.).
На многомерные случайные величины распространяются почти без изменений основные определения, относящиеся к одномерным случайным величинам.
4.1.1. Дискретная двумерная случайная величина.
Рассмотрим двумерную
дискретную случайную величину
![]() Ее двумерное распределение можно
представить в виде таблицы,
Ее двумерное распределение можно
представить в виде таблицы,
|
Y X |
|
. . . |
|
... |
|
|
|
|
|
. . . |
|
. . . |
|
|
|
. . . |
. . . |
|
. . . |
|
. . . |
. . . |
|
|
|
. . . |
|
. . . |
|
|
|
. . . |
. . . |
|
. . . |
|
. . . |
. . . |
|
|
|
. . . |
|
. . . |
|
|
|
|
|
|
|
|
|
1 |
содержащей в
соответствующих клетках вероятности
произведения событий
![]() (или вероятность того, что случайный
вектор (
(или вероятность того, что случайный
вектор (![]() примет значение (
примет значение (![]() ).
).
Итоговые столбец
и строка такой таблицы задают распределения
одномерных составляющих
![]() или
или
![]() ,
называемых маргинальными.
,
называемых маргинальными.
Действительно,
распределение одномерной случайной
величины X
можно
получить, вычислив по данным таблицы
вероятности
![]() которые обозначим через
которые обозначим через
![]() .
Но случайное событие
.
Но случайное событие
![]() можно представить как сумму попарно
несовместных событий:
можно представить как сумму попарно
несовместных событий:
![]()
откуда по формуле полной вероятности получим
![]() ,
,
![]()
Аналогично ![]() ,
,
![]() .
.
Так как события![]()
![]() образуют полную систему, то сумма
вероятностей, помещенных во всех клетках
таблицы, равна единице.
образуют полную систему, то сумма
вероятностей, помещенных во всех клетках
таблицы, равна единице.
Пример 1. В группе 10 студентов, а именно
![]() ,
где римской цифрой обозначен курс, на
котором учится студент, а индексы m
и f
обозначают
пол – соответственно мужской и женский.
Определим случайные величины Х-{пол
студента},
Y-{курс
обучения}.
Тогда возможные значения Х
= 0 для
f,
X
=
1
для m,
Y
=
0
для I,
Y
=
1
для II
и т.д., т.е. Х
принимает значения от 0 до 1, а Y-
от 0 до 3.
,
где римской цифрой обозначен курс, на
котором учится студент, а индексы m
и f
обозначают
пол – соответственно мужской и женский.
Определим случайные величины Х-{пол
студента},
Y-{курс
обучения}.
Тогда возможные значения Х
= 0 для
f,
X
=
1
для m,
Y
=
0
для I,
Y
=
1
для II
и т.д., т.е. Х
принимает значения от 0 до 1, а Y-
от 0 до 3.
Нас интересуют
вероятности вида
![]() i=1,2;
i=1,2;
![]() .
Все варианты возможных исходов и их
совместные вероятности приведены в
таблице
.
Все варианты возможных исходов и их
совместные вероятности приведены в
таблице
|
Y X |
0 |
1 |
2 |
3 |
|
|
0 |
0,1 |
0,1 |
0,1 |
0,1 |
0,4 |
|
1 |
0,2 |
0,2 |
0,1 |
0,1 |
0,6 |
|
|
0,3 |
0,3 |
0,2 |
0,2 |
1,0 |
Маргинальные распределения имеют вид:
|
X |
0 |
1 |
|
|
Y |
0 |
1 |
2 |
3 |
|
|
|
0,4 |
0,6 |
1,0 |
|
|
0,3 |
0,3 |
0,2 |
0,2 |
1,0 |
Рассмотрим
распределение одной из случайных
величин, например, X
при
определенном значении другой
![]() .
Для этого необходимо вычислить условные
вероятности событий
.
Для этого необходимо вычислить условные
вероятности событий
![]() при наступлении события
при наступлении события
![]() Обозначив эти условные вероятности
через
Обозначив эти условные вероятности
через
![]() ,
,
![]()
![]() ,
получим из определения условных
вероятностей
,
получим из определения условных
вероятностей
![]()
![]() .
.
Таким образом,
разделив все элементы k-го
cтолбца
таблицы на итоговую вероятность по
этому
столбцу
![]() ,
получим условное распределение X
при
,
получим условное распределение X
при
![]() .
.
Аналогично по
формуле
![]()
определим условные
вероятности значений Y
при
данном значении
![]() .
.
Сумма вероятностей
условного распределения равна 1. Продолжим
пример. Найти распределение по половому
признаку студентов 2-го курса, т.е.
при![]() .
Выбрав второй столбец из совместного
распределения и разделив его на
.
Выбрав второй столбец из совместного
распределения и разделив его на
![]() ,
получим требуемое распределение
,
получим требуемое распределение
|
X |
0 |
1 |
|
|
|
1/3 |
2/3 |
1,0 |
Аналогично находим распределение студенток по курсам обучения. Например, для первого
|
Y |
0 |
1 |
2 |
3 |
|
|
|
0,25 |
0,25 |
0,25 |
0,25 |
1,0 |
Пример 2. Пусть совместное распределение
![]() i =
1,2,3; k
=
1,2,3 случайных
доходов (в долларах) фирм Х
и
Y в течение
некоторого дня задано таблицей (без
i =
1,2,3; k
=
1,2,3 случайных
доходов (в долларах) фирм Х
и
Y в течение
некоторого дня задано таблицей (без
![]() и
и
![]() )
)
|
Y X |
-100 |
0 |
100 |
|
|
-200 |
0,20 |
0,10 |
0,05 |
0,35 |
|
0 |
0,05 |
0,25 |
0,02 |
0,32 |
|
200 |
0,01 |
0,02 |
0,30 |
0,33 |
|
|
0,26 |
0,37 |
0,37 |
1,0 |
Найти:
а) Маргинальное
распределение
![]() и
и
![]() .
.
б) Распределение дохода фирмы Y, если фирмой Х был получен доход Х=200$.
в) Средний доход
![]() .
.
Решение:
а)
|
X |
-200 |
0 |
200 |
|
|
Y |
-100 |
0 |
100 |
|
|
|
0,35 |
0,32 |
0,33 |
1,0 |
|
|
0,26 |
0,37 |
0,37 |
1,0 |
б)
|
Y |
-100 |
0 |
100 |
|
|
|
|
|
|
1,0 |
в)
![]() $.
$.
