19. Исследование функций

1. Найти наибольшее и наименьшее значения функции на отрезке .

Решение

Функция достигает наибольшего и наименьшего значений либо в точках, подозрительных на экстремум, либо на концах отрезка.

2.Исследовать функцию на экстремум

.

Решение

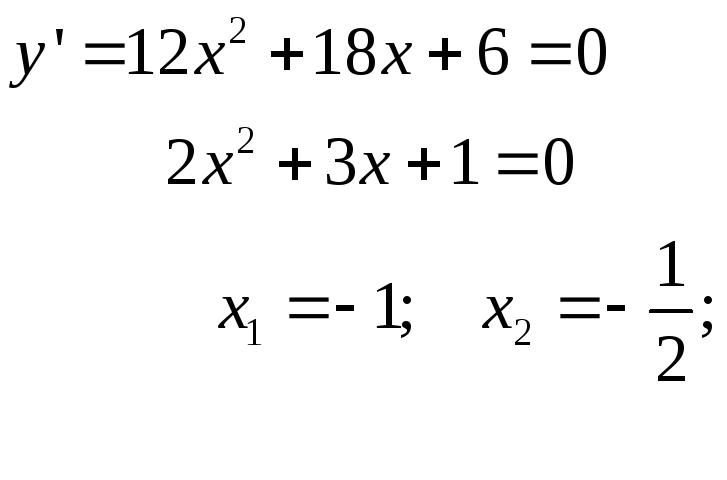
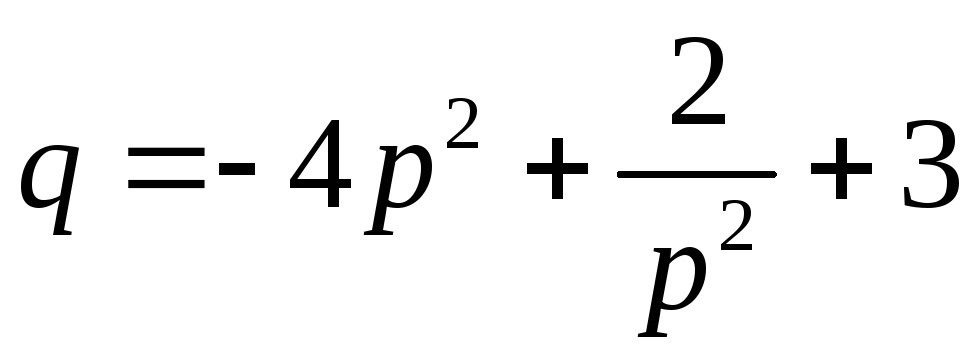3. Эластичность спроса относительно цены находится по формуле , где . Найти , если , (у. е.).

Решение

Задания для самостоятельной работы

1. Найти наибольшее и наименьшее значение функции у = 2х⁴– 4х² + 1 на отрезке [-2; 3].

2. Исследовать функцию у = 2х⁴– 4х² + 1 на экстремум.

Ответы:

1. у_наим. = -1 в точке х = -1 и х = 1, у_наиб. = 127 в точке х = 3.

2. х = -1, х = 1 – точки минимума; х = 0 – точка максимума.

20. Частные производные функции двух независимых переменных

1. Найти частные производные первого порядка функций:

а) ; б) .

Решение

а) чтобы найти , считаем постоянной величиной и дифференцируем как функцию одной переменной :

.

Аналогично, считая постоянной величиной, находим :

;

б) ;

.

2. Найти полный дифференциал функции .

Решение

Так как , то по формуле полного дифференциала находим

.

3. Найти частные производные второго порядка функции

.

Решение

Частные производные первого порядка для данной функции:

.

Дифференцируя и по переменным х и y, получим

,

;

;

.

4. Найти стационарные точки функции двух переменных

.

Решение

Стационарная точка – это точка, в которой частные производные первого порядка равны нулю:

,

Ответ: стационарная точка .

5. Найти градиент функции в точке .

Решение

Задания для самостоятельной работы

1. Найти стационарные точки функции двух переменных .

2. Найти частные производные первого порядка функций:

а) ; б) ; в) .

Ответы:

1. и .

2. а) ; ;

б) ; ;

в) ; .

21. Неопределенный интеграл. Замена переменной

в неопределенном интеграле. Интегрирование по частям

1.

2. .

3.

4. .

Задания для самостоятельной работы

1. .

2. .

3.

4.

Ответы: 1. 2. .

3. 4. .

22. Определенный интеграл.

Интегрирование по частям в определенном интеграле

1. Производительность труда в течение рабочего дня определяется функцией , где время. Определить объем продукции , произведенной рабочим за 6-ти часовой рабочий день, если .

Решение

.

Ответ: 462.

2. Найти площадь, ограниченную параболой и осью абсцисс.

Решение

Найдем точки пересечения параболы и оси абсцисс.

3х - х² =0  х(3 – х) = 0  х = 0, х = 3.

Следовательно, в формуле

а = 0, b = 3, y₂ = 3x – x², y₁ = 0.

(кв.ед.).

Ответ: (кв.ед.).

3. Вычислить интеграл .

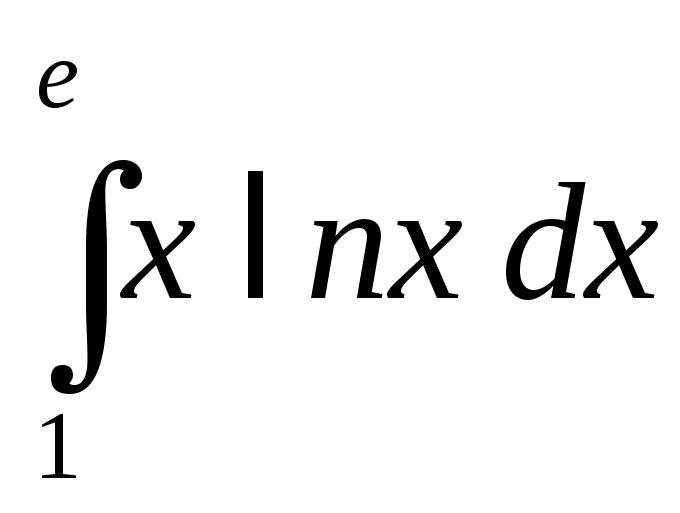Решение

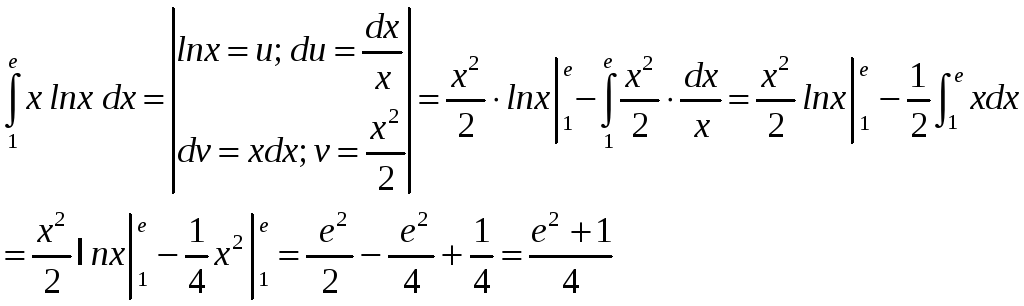
Задания для самостоятельной работы

1. Найти площадь фигуры, ограниченной графиками функции:

y = 2 – x² и y = x .

2. Вычислить интеграл .

3. Вычислить интеграл .

4. Вычислить интеграл .

Ответы:

1. 4,5 кв.ед.

2. 0.

3. .

4. 2 (2 - ln3).