6. Проекция вектора на ось
1.
Даны четыре точки: А
(3; 0; 2); В
(1; 3; –2); С
(–1; 0; 4); D
(2; 3; 4). Найти проекцию вектора
на вектор
,
а также проекцию
на
.
Решение
Пусть
(лин.
ед.).
(лин.ед.).
Ответ:
,
.
2.
Даны два вектора
(3;
4; 2),
(1;
1; 2). Найти проекцию вектора
на вектор
Решение
Найдем координаты векторов
и
.
.
.
Следовательно:
(лин.ед.).
Задания для самостоятельной работы
1.
Даны векторы
(3; 2; 1) и
(4;
0; 5). Найти проекцию вектора
на вектор
.
2.
Даны точки А
(3; 3; –2), В
(0; –3; 4), С
(0; –3; 0), D
(0; 2; –4). Найти проекцию
на
.
3.
Даны векторы
(1; -2; 4) и
(2; 4; -4). Найти длину вектора
.
Ответ:
1.
.
2.-6.
3. 12.
7. Прямая линия на плоскости
1. Вычислить площадь треугольника, заключенного между осями координат и прямой 7х + 2у – 14 = 0.
Решение
Преобразуем общее уравнение прямой к уравнению прямой в отрезках на осях.
7
.
Таким
образом, а=2,
b=7.
Следовательно,
(кв.
ед.).
Ответ: 7.
2. Составить уравнение прямых, проходящих через середины сторон треугольника с вершинами
А (1; 4); В (3; –2), С (5; – 4).
Решение
Найдем
середины сторон треугольника
:
– середина
АВ,
– середина
АС,
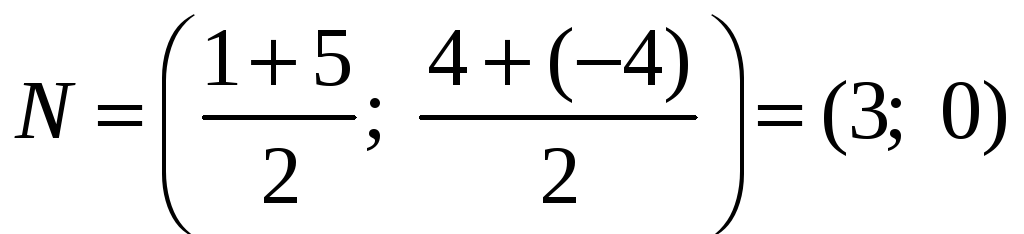– середина
ВС.
Тогда, используя уравнение прямой, проходящей через две точки, имеем:
прямая
MN:
прямая
МР:
прямая
NP:
3.Найти угол между прямыми:
Решение
Пусть
Тогда по формуле
находим
4. Дан треугольник с вершинами А (–3; 5), В (0; 4), С (–1; 8). Найти длину высоты, опущенной из точки В.
Р
Высота ВК равна расстоянию от точки В до прямой АС. Найдем общее уравнение прямой АС.
Вначале построим уравнение прямой АС как уравнение прямой, проходящей через точки А и С:
3х + 9 = 2у – 10 –3х + 2у – 19 = 0
– общее
уравнение прямой АС
.
Теперь,
используя формулу
,
получаем:
3,06.
(мы
подставили в формулу координаты точки
В
и вектора
).
Задания для самостоятельной работы
1. Вычислить площадь треугольника, заключенного между осями координат и прямой 5х - 2у – 10 = 0.
2.
Найти угол между прямыми
и
.
3. Найти длины отрезков, отсекаемых прямой 3х - 5у – 15 = 0 на осях координат.
4. Написать уравнение прямой, проходящей через точку А(1; 5) параллельно прямой 2х - 3у + 4 = 0.
Ответы: 1. 5.
2.
.
3. 5.
4. 2х - 3у + 13 = 0.
8. Прямая линия в пространстве
1. Составить параметрические и канонические уравнения прямой, проходящей через точку М0 (3; – 4; 2) параллельно прямой:
.
Решение
Из
уравнения заданной прямой выпишем
вектор
(4;
–2; 3) — направляющий вектор прямой. Он
же является направляющим и для прямой,
уравнение которой мы должны построить.
Итак, х0
= 3, у0
= –4, z0
= 2 – координаты точки М0;
m
= 4, n
= –2, p
= 3 – координаты направляющего вектора.
Имеем:
— параметрические
уравнения прямой.
Выражая параметр из этих уравнений, получим канонические уравнения искомой прямой
.
Ответ:
,
.
2. Составить канонические уравнения прямой в пространстве, если известно, что она проходит через точки А(2; 3; -5), В(-1; 4; 0).
Решение
Воспользуемся уравнением прямой, заданной двумя точками
.
Следовательно
.
Упрощая, получаем канонические уравнения
прямой
.
Задания для самостоятельной работы
1. Написать канонические уравнения прямой, проходящей через точки А(1; 2; 3), В(4; 5; 8).
-
Написать уравнение прямой, проходящей через точку М (2; 3; -4) перпендикулярно плоскости 3х - 4у + 2z – 1 = 0.
Ответы:
1.
.
2.
.