1. Матрицы. Действия с матрицами

1. Найти матрицу , если

Решение

;

.

Ответ: .

2. Найти матрицу , удовлетворяющую уравнению , если

, .

Решение

; .

Ответ: .

3. Даны матрицы . Выяснить, существуют ли произведения и , и если существуют, найти их.

Решение

Матрица имеет размер , матрица имеет размер . Матрицы и согласованные, поэтому матрица – произведение существует и имеет размер . Произведение также существует и имеет размер .

Ответ:

Задания для самостоятельной работы

1. Вычислить , если

, , .

2. Найти , если

3. Найти матрицу Х, если ,

где

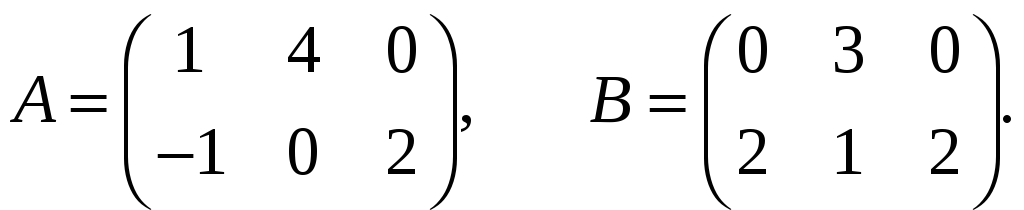
Ответы:

1. .

_2..

3. .

2. Обратная матрица и ее вычисление

1. Найти матрицу, обратную матрице , если

Решение

,

Ответ:

Задания для самостоятельной работы

Найти обратную матрицу:

а) ; б) ; в) ; г) .

Ответы:

а) ; б) ; в) ; г) .

3. Определители и их свойства

Найти определитель

1. .

2.

3. Решить уравнение

Решение. Вычислим определитель по правилу треугольников:

Ответ:

Задания для самостоятельной работы

С помощью правила треугольников вычислить определители

а) ; б) ; в) г) .

Ответы:

а) –25; б) 168; в) 21; г) 12.

4. Системы линейных алгебраических уравнений

1. Решить систему линейных алгебраических уравнений матричным способом

Решение

Основная матрица системы: .

Так как , то существует обратная матрица , и, следовательно, исходная система имеет единственное решение .

==.

Транспонируя матрицу , получим присоединенную матрицу

==.

Найдем решение исходной системы, учитывая, что В = .

= = В = ּ = = .

Ответ:

2. Решить систему линейных алгебраических уравнений по формулам Крамера

Решение. Вычислим главный определитель системы:

Вычислим побочные определители системы

По формулам Крамера получаем

Ответ:

3. Решить систему линейных алгебраических уравнений методом Гаусса

Решение

.

Ответ:

Задания для самостоятельной работы

Решить систему линейных алгебраических уравнений матричным способом и по формулам Крамера.

а) 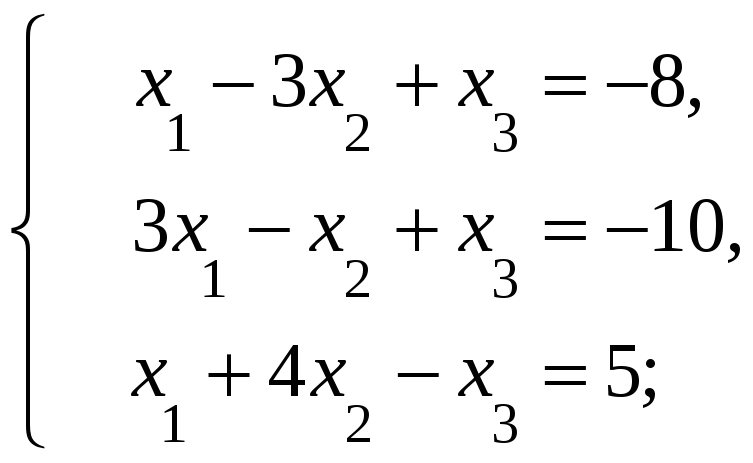б)

Ответ: а) ; б) система несовместна.

5. Векторы. Скалярное, векторное, смешанное произведения векторов

1. Даны векторы , .

Найти угол между ними.

Решение

Векторы и имеют координаты .

Ответ: .

2. При каком значении векторы и ортогональны, если

.

Решение

Так как , то составим скалярное произведение векторов и приравняем его нулю.

.

Ответ: .

3. Вычислить , если .

Решение

Ответ: 8.

4. Выяснить, является ли данная система векторов линейно зависимой или независимой:

.

Решение

Проверим, являются ли векторы компланарными. Найдем смешанное произведение векторов.

Смешанное произведение векторов равно нулю, векторы компланарны, значит, система векторов линейно зависима.

Ответ: линейно зависима.

5. Даны векторы . Найти их векторное произведение, синус угла между ними и площадь параллелограмма, построенного на этих векторах.

Решение

(кв.ед.)

Чтобы найти синус угла между векторами и , найдем их длины:

Следовательно:

Ответ: , , (кв.ед.).

6. Определить угол А в ∆АВС с вершинами А (1; 1; 1), В (2; –1; 3),

С (0; 0; 5).

Решение

Так как , то (из координат конца вектора вычитаем координаты начала).

Ответ: .

Задания для самостоятельной работы

1. Найти векторное произведение векторов

, .

2. Определить угол B в ∆АВС с вершинами А (1; 1; 1), В (2; –1; 3),

С (0; 0; 5).

3. Вычислить площадь треугольника с вершинами А (3; 0; –4),

В (–1; 0; 2), С (1; –2; 5).

Ответ: 1. .

2. .

3. .