1.8. Развертки поверхностей геометрических тел.

Разверткой многогранника называется плоская фигура, состав­ленная из его граней развернутых на одну плоскость.

Развертка призмы. Для развертки призмы применяют два метода нормального се­чения и раскатки.

М

Рис. 1. 98

етод нормального сечения. Построим развертку наклонной трехгранной призмы ABCDEF с помощью данного метода. (Рис. 1.98)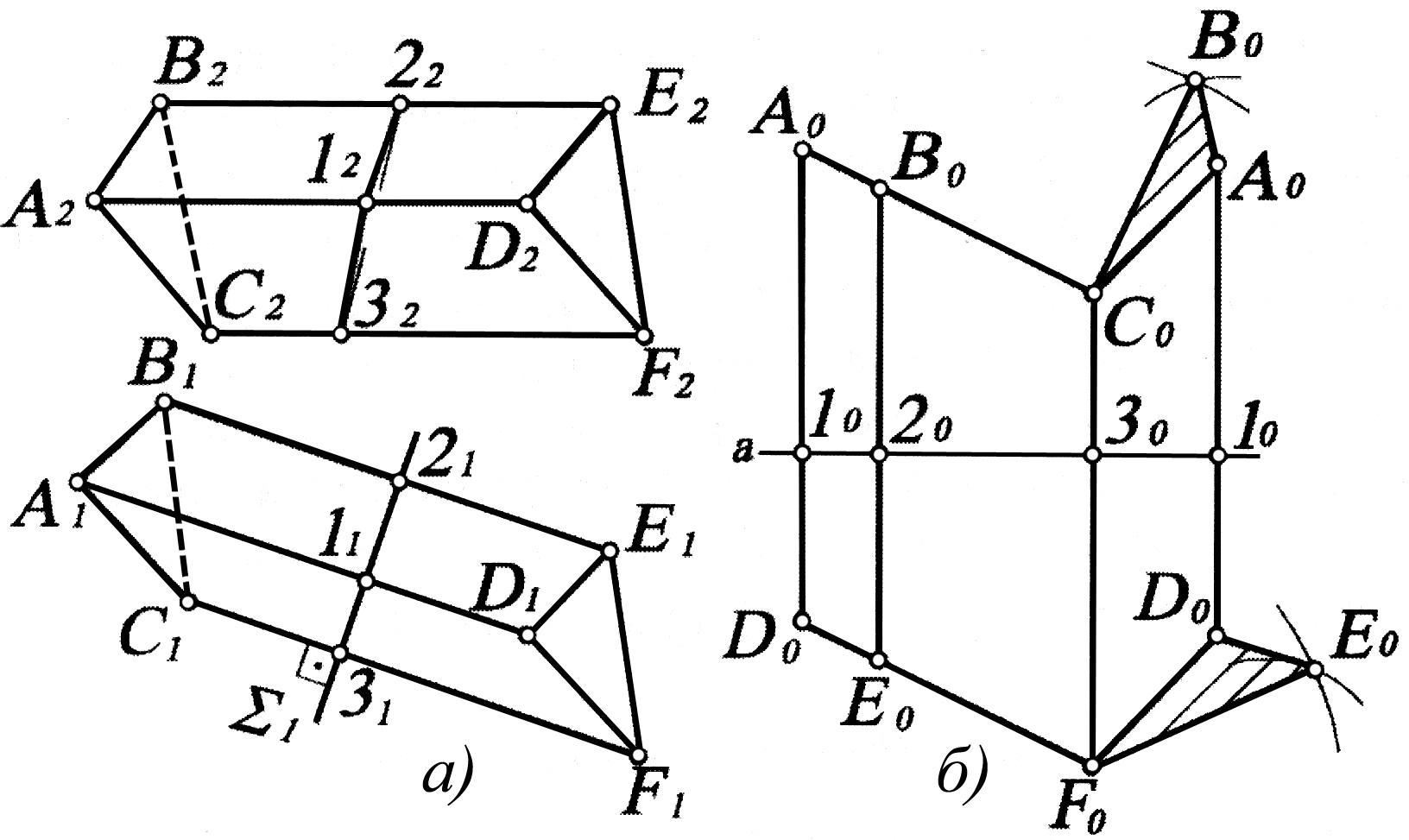

Пересечем призму ABCDEF плоскостью  перпендикулярной к ее боковым ребрам. Построим сечение заданной призмы этой плоскостью - треугольник 123 и определим его стороны. В свободном поле чертежа проведем прямую линию а (см. рис. 1.98 - прямая линия проведена горизонтально). От произвольной точки 1₀, взятой на этой прямой отложим отрезки 1₀2₀, 2₀3₀, 3₀1₀, равные сторонам треугольника 123. Че­рез точки 1₀, 2₀, 3₀, 1₀ проведем прямые, перпендикулярные прямой а, и отложим от точек 1₀, 2₀, 3₀, 1₀ отрезки, равные соответствующим длинам боковых ребер (1А, ID, 2В, 2Е, … ). Полученные точки А₀, В₀, С₀, А₀ и D₀, E₀, F₀, D₀ соединяем прямыми. Плоская фигура А₀В₀С₀А₀D₀E₀F₀D₀ представляет собой развертку боковой поверхности призмы.

Чтобы получить полную развертку призмы необходимо к раз­вертке боковой поверхности пристроить основания призмы – треугольники ABC и DEF, предварительно определив их неискаженные размеры (натуральную величину).

Метод раскатки. Раскатываем боковую поверхность призмы на плоскости черте­жа одну грань за другой.

У

Рис. 1. 99

добнее всего рассмотреть применение метода раскатки на при­мере развертки прямой пятигранной призмы частного положения. (Рис. 1.99)

Поскольку боковые грани призмы представляют собой горизон­тально проецирующие плоскости, то ребра основания проецируют­ся в натуральную величину на П₁, а длину боковых ребер можно измерить на П₂. Таким образом, имеем длину каждого ребра, чтобы раскатать все грани на плоскости чертежа. При этом, очевидно, что высота каждой боковой грани равна любому боковому ребру. Отме­тим в произвольном месте чертежа точку А₀ на горизонтальной линии. Затем строим последовательно В₀, С₀, D₀, E₀, А₀, перенося на эту линию длину отрезков А₁В₁, В₁С₁, С₁D₁, D₁E₁, E₁ А₁ соответственно. В результате раскатываем все боковые грани призмы.

Остается достроить на одной из сторон, например D₀E₀, ниж­нее основание А₀В₀С₀А₀D₀E₀А₀ (см. рис. 1.99) Это легко сделать, разбив пятиугольник А₁В₁С₁D₁E₁ на треугольники.

Тогда, например, точка А₀ будет лежать на пересечении дуг окружностей, проведен­ных радиусом E₁A₁ из точки E₀ и радиусом D₁A₁ из точки D₀. В том случае, когда призма занимает общее положение в пространстве, необходимо сначала определить натуральную величину каждого ребра одним из способов преобразования чертежа, а затем вычертить развертку призмы одним из вышеописанных методов.

Развертка цилиндра. Из всех поверхностей построение развертки возможно лишь для линейчатых поверхностей вращения. Например, цилиндр и конус. Развертку сферы и тора построить нельзя.

Построение развертки цилиндра и конуса осуществляется в оди­наковой последовательности. Сначала раскатываем боковую повер­хность, а затем достраиваем основание.

Р

Рис. 1.100

ассмотрим построение развертки прямого цилиндра. (Рис. 1.100)

Решение получить несложно ввиду того, что боковая поверхность цилиндра перпендикулярна к П₁. Развертка боковой поверхности пря­мого цилиндра представляет собой прямоугольник, высота которого Н равна длине образующей A₂A₂*, изображенной на П₂, а ширина длине окружности 2πR, где R - радиус основания конуса, заданного без искажений на П₁. Остается дополнить чертеж разверткой основа­ния, которая полностью совпадает с его горизонтальной проекцией. При этом точка К касания основания выбирается произвольно на длинной стороне полученного прямоугольника.

Р

Рис. 1.101

азвертка прямого конуса. (Рис. 1.101) Боковая повер­хность разворачивается в сектор окружности радиуса S₀A₀, равного длине образующей конуса.

В данном примере длина образующей конуса L = S₀A₀= S₂A₂, так как SA параллельна П₂. Центральный угол сектора вычисляется по формуле:

α =2πR/2πL ∙360=R/L ∙360,

где L = 2R, поэтому α = 180°. Тогда развертка боковой поверх­ности представляет собой половину круга радиуса L. Чтобы получить полную развертку прямого конуса, нужно достроить основа­ние, равное площади круга радиуса R, причем таким образом, что­бы этот круг касался развертки боковой поверхности в некоторой точке К.

Оба рассмотренных здесь примера позволяют получить доста­точно простое решение. Однако задача усложняется, когда необхо­димо построить развертку, например, наклонного конуса, располо­женного по отношению к плоскостям проекций произвольным об­разом. Тогда приходится производить построение по точкам, характеризующим натуральную величину переменной образующей. Основание в этом случае представляет собой эллипс.