1.5. Способы преобразования ортогонального чертежа.

Способы преобразования чертежа служат для решения метри­ческих задач по определению натуральной величины геометричес­ких объектов (отрезка прямой или плоскости), либо кратчайшего расстояния между геометрическими объектами.

Суть этих способов заключается в том, что необходимо преоб­разовать комплексный чертеж так, чтобы рассматриваемый геометрический объект занял положение, параллельное какой-либо плос­кости проекций, на которую он проецируется в натуральную вели­чину.

Такое преобразование комплексного чертежа может быть, осу­ществлено двумя основными способами:

- Способам вращения, при котором оставляют неизменной сис­тему плоскостей проекций, а меняют положение заданного геометрического объекта путем его вращения вокруг одной или последо­вательно вокруг двух подходящим образом выбранных осей так, что­бы интересующие нас прямые или плоскости оказались параллельными одной из плоскостей проекций. В качестве оси вра­щения обычно выбирают прямую, перпендикулярную одной и из плос­костей проекций.

- Способ плоскопараллельного перемещения является способом вращения вокруг проецирующей оси, с той лишь разни­цей, что геометрический объект можно не только вращать, но и пере­мещать вдоль плоскости, параллельной одной из плоскостей проек­ции. Этот способ используется при решении задач на перемещение прямой линии в положение прямой уровня или проецирующей и преобразования плоскости общего положения в проецирую­щую или в плоскость уровня.

- Способом замены плоскостей проекций, при котором оставляют неизменным положение в пространстве геометрического объек­та, а заменяют одну или последовательно две плоскости проекций так, чтобы интересующие нас прямые или плоскости оказались па­раллельными одной из новых плоскостей проекций.

Этими способами также можно решать задачи ни приведение геометрических объектов в проецирующее положение.

- Способом совмещения. Если плоскость вращать вокруг ее сле­да до совмещения с плоскостью проекций, в которой располо­жен этот след, то геометрические образы, расположенные в плоскости, изобразятся без искажения.

Способ вращения вокруг проецирующей оси.

Вращение точки. Рассмотрим вращение точки А вокруг оси i, перпендикулярной горизонтальной плоскости проекций П₁ (рис. 1.50). Ось вращения про­ецируется на плоскость П₁ в точку, а на плоскость П₂ - в прямую, перпендикулярную оси ОХ. Траекторией движения точки А б

Рис. 1.50

удет ок­ружность, лежащая в плоскости вращения, параллельной плоскости П₁, с центром вращения в точке О, лежащей на оси, и с радиусом вращения ОА (рис. 1.50, а). Траектория движения точки проецирует­ся на плоскость П₁ в натуральную величину, а на плоскость П₂ - в виде прямой, параллельной оси ОХ. Радиус окружности также про­ецируется на плоскость П₁ в натуральную величину. Таким образом, горизонтальная проекция A₁ точки А движется по окружности, а фрон­тальная проекция A₂ - по прямой, параллельной оси ОХ.

Для того, чтобы повернуть точку А на угол φ, откладывают этот угол на горизонтальной проекции (рис. 1.50, б) и получают горизон­тальную проекцию A₁ точки A в новом положении A₁*. Фронтальную проекцию А₂* этой точки находят с помощью линии проекционной связи которую проводят из точки A₁* до пересечения с прямой, про­веденной из точки A₂ параллельно оси ОХ.

Вращение прямой линии. Так как прямая линия однозначно определяется двумя точками, то вращение прямой сводится к вращению точек, расположенных на прямой.

Построения выполняется проще, если ось вращения проходит че­рез одну из конечных точек отрезка прямой. Эта точка при вращении остается неподвижной, поэтому достаточно повернуть любую дру­гую точку этой прямой чтобы найти новое ее положение. Например, чтобы определить длину отрезка AВ прямой общею положения, проведем ось вращения i через точку В перпендикулярно например, П₁ и повернем отрезок АВ так, чтобы он стал параллелен плоскости П₂, т. е. занял положение фронтали. Точка В остается неподвижной (рис. 1.51), точку A₁ пов

Рис. 1.51

орачиваем на некоторый угол φ, при этом горизонтальная проекция A₁*В₁ повернутого отрезка AВ расположится параллельно оси ОХ. Длина его фронтальной проекции A₂*В₂, будет равна длине отрезка АВ, т. к. А*В занимает положение фронтали.

При этом угол α - угол наклона АВ к П₁, так как при вращении прямой вокруг оси, перпендикулярной какой-либо плоскости про­екций, угол наклона к этой плоскости не изменяется. Длину отрезка прямой можно найти также вращением вокруг оси расположенной перпендикулярно П₂. При этом определяется угол наклона β прямой АВ к плоскости П₂.

П

Рис. 1.52

реобразование прямой линии (способом перемещения). При перемещении отрезка прямой в новое положение таким образом, что его крайние точки движутся параллель­но какой-либо плоскости проекций, длина проекции отрезка на эту плос­кость остается неизменной. (Рис. 1.52)

Преобразуем последовательно от­резок прямой линии общего положе­ния АВ сначала в положение горизон­тали, затем во фронтально-проециру­ющее. Для этого расположим фронтальную проекцию А₂В₂ отрезка АВ параллельно оси ОХ (А₂*В₂*ОХ) в любом месте чертежа. При этом точки А₁ и В₁ перемещаются в новое положение по прямым, параллельным оси ОХ, и будут ле­жать на линиях связи с A₂*, В₂* соответственно. Тогда новая гори­зонтальная проекция займет положение A₁*В₁*. Очевидно, что A₁*В₁* - натуральная величина отрезка АВ, т. к. А*В* является горизонта­лью. Затем A₁*В₁* переместим в новое положение, чтобы A₁**В₁** была перпендикулярна оси ОХ. Тогда A₂**=В₂**, т. е. АВ займет по­ложение проециру­ющей прямой. Сле­дует заметить, что при определении на­туральной величины АВ, которой соответ­ствует длина A₁*В₁*, удаленность проек­ции А₂*В₂* от оси ОХ не играет роли. Важно лишь выполнение двух требова­ний: А₂*В₂* должна быть равна А₂В₂ и параллельна оси ОХ.

П

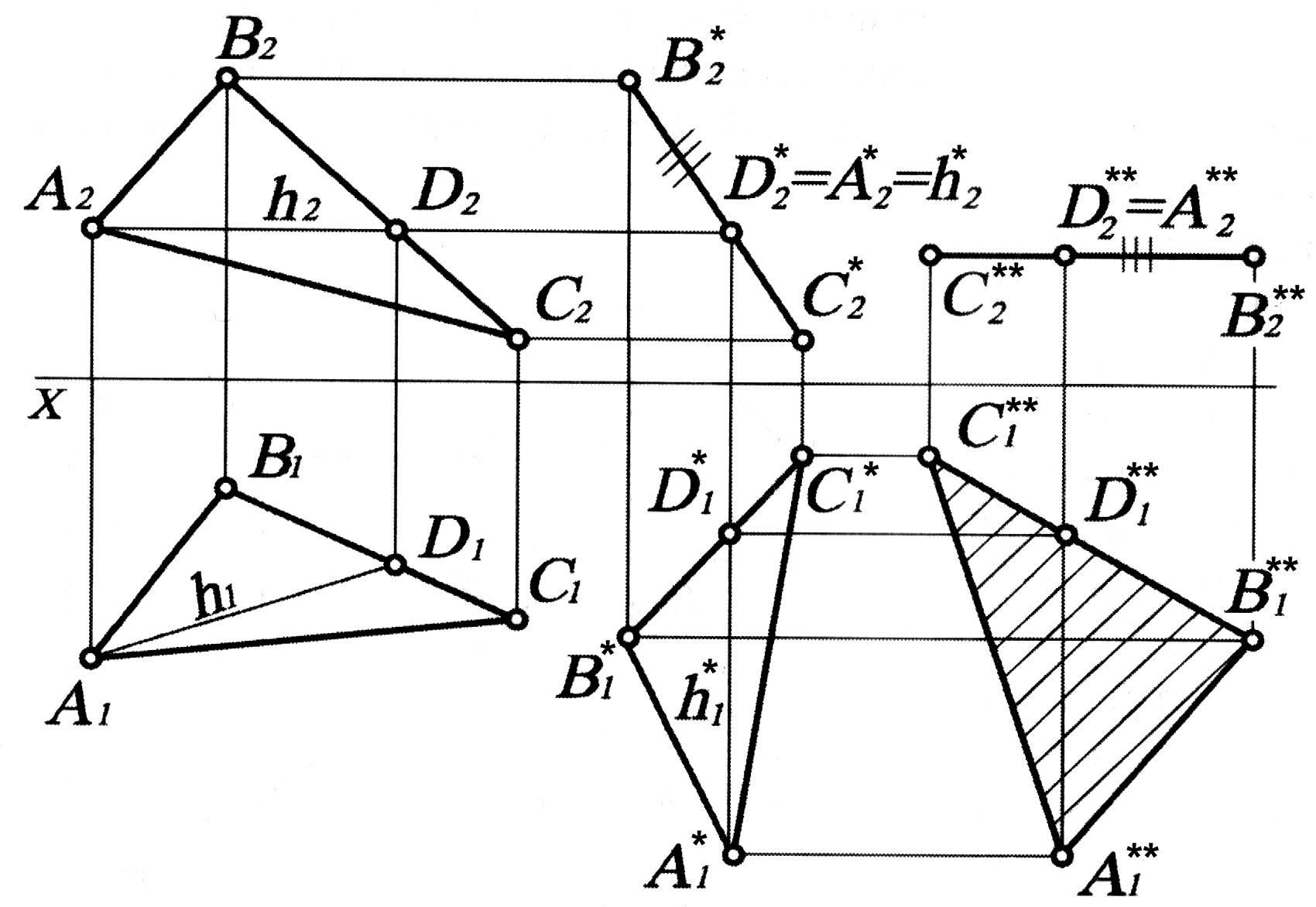Рис. 1.53

реобразование плоскости. Преобразуем плоскость ABC общего положения (рис. 1.53) в горизонтальную плоскость уровня. Одним преобразованием черте­жа эту задачу решить невозможно в рамках рассматриваемого спо­соба. Найдем решение, осуществив два перемещения ABC внача­ле, приведем его в проецирующее положение, а затем - в положение плоскости уровня.

Переместим плоскость ABC, например во фронтально-проеци­рующее положение, которое характеризуется тем, что горизонталь этой плоскости должна быть перпендикулярна П₂. Следовательно, сначала необходимо в плоскости ABC построить горизонталь, а затем переместить ее в новое положение так, чтобы горизонталь­ная проекция h₁ горизонтали стала перпендикулярна оси ОХ. При этом горизонтальная проекция  А₁В₁С₁ перемещается в новое по­ложение, не меняя своей величины. Поэтому построения на первом этапе осуществляются в следующей последовательности вначале перемещаем в новое положение А₁В₁С₁. Для этого на некотором расстоянии от него проводим перпендикуляр к ОХ на нем откладываем длину A₁*D₁* = A₁D₁, причем точку А₁* строим на произвольном расстоянии от ОХ. Далее необходимо перенести  А₁В₁С₁ в новое положение, не меняя его размеров, совместив h₁ и h₁*. Для этого до­статочно из точки А₁* провести дугу радиуса А₁С₁, а из точки D₁* — радиуса D₁С₁. На месте пересечения дуг получим точку С₁*. Анало­гично перенесем В₁ в положение В₁*.

Таким образом получаем ABC, в новом положении A₁*В₁*С₁*. Очевидно, что при этом фронтальные проекции точек А, В, С пере­мещаются по прямым, параллельным оси ОХ, и займут место на ли­ниях связи с точками A₁*, В₁*, С₁* соответственно. Поскольку ABC должен занять фронтально-проецирующее положение, его проекция A₂*В₂*С₂* представляет собой прямую.

Второе перемещение осуществляют так, чтобы ABC занял по­ложение горизонтальной плоскости уровня. Тогда его фронталь­ная проекция A₂**В₂**С₂** должна быть параллельна оси ОХ. Для этого отрезок В₂*A₂*С₂* перемещают на свободное поле чертежа, не меняя его длину. Получаем С₂** A₂**В₂** параллельный оси ОХ. А каждая из точек A₁*, В₁*, С₁* смещается по прямым, параллельным оси ОХ, до положения на линиях связи с точками A₂**, В₂**, С₂** соответственно.

Полученный A₁**В₁**С₁** " и есть натуральная величина  ABC, поскольку он является горизонтальной проекцией горизонтальной плоскости уровня.

Способ замены плоскостей проекций состоит в том, что одна из основных плоскостей проекций П₁ или П₂ заменяется новой плоско­стью - П₄, подходящим образом расположенной относительно изоб­ражаемого геометрического объекта, но перпендикулярной незаме­няемой плоскости проекций.

В результате замены одной из основных плоскостей на плоскость проекций П₄ получаем вместо старой системы плоскостей проекций П₁/П₂ новую систему П₁/П₄ (рис. 1.54), если заменялась плоскость П₂, и систему П₂/П₄, если заменялась плоскость П₁.

Например, на рис. 1.54, а плоскость П₄ может выступать в роли фронтальной плоскости проекций П₂. На рис. 1.54, б прямыми z_A отмечены р

Рис. 1.54

асстояния от точки А до горизонтальной плоско­сти проекций П_1. Естественно (см. рис. 1.54, а), эти расстояния равны А₂А₁₂ = А₄А₁₄, так как высота точки А над плоскостью П₁ проецирует­ся как на П₂, так и на П₄ в виде одинаковых отрезков. Расстояние же до П₂ и П₄ от точки А могут быть различными, поэтому А₁А₁₂А1А14. Способ замены плоскостей проекций рационально применять при решении задач по определению натуральной величины:

а) отрезка прямой линии,

б) натуральной величи­ны плоской фигуры;

в) натуральной величи­ны двугранного угла,

г) кратчайшего рассто­яния от точки до прямой линии или до плоскости;

д) кратчайшего рассто­яния между двумя парал­лельными или двумя скрещивающимися прямыми.

Решение задач данным способом рассмотрим на следующих примерах.

О

Рис. 1.55

пределение длины отрезка общего положения. Для определения натуральной величины (длины) отрезка АВ прямой линии общего положения необходимо сделать этот отрезок в новой системе плоскостей проекций линией уровня. Для этого заменим плоскость П₂ на плоскость П₄ параллельную АВ, и перейдем от системы П₁/П₂ к системе П₁/П₄. Новую ось проекций X₁₄ вы­бираем параллельно A₁В₁. (Рис. 1.55) Для построения новой проек­ции отрезка АВ проводим новые линии проекционной связи пер­пендикулярно оси X₁₄ и отмечаем на них новые проекции A₄, B₄ точек А и В. Для этого откладываем А_x1А₄ = A₂ A_x; В_x1В₄ = В₂В_x.

Соединяя найденные точки A₄В₄, получаем новую проекцию А₄В₄ отрезка АВ. Как видим, отрезок АВ в системе плоскостей проекций П₁/П₄ является линией уровня, так как A₁В₁ параллельна X₁₄, а следова­тельно, АВ параллельна П₄. Тогда очевидно, что А₄В₄ является нату­ральной величиной отрезка АВ.

Определение натуральной величины плоской фигуры. Для определения натуральной величины плоской фигуры необ­ходимо дополнительную плоскость построить так, чтобы она была параллельна рассматриваемой фигуре, и тогда на эту плоскость про­екций плоская фигура проецируется в натуральную величину. Если в качестве плоской фигуры выбрать треугольник, тогда задача фор­мулируется следующим образом: преобразовать плоскость треугольника общего положения в новой системе плоскостей проекций в плос­кость уровня.

Одной заменой плоскостей проекций эту задачу решить невоз­можно, так как необходимо соблюдать условие: новая плоскость дол­жна быть перпендикулярна незаменяемой. Поэтому решим эту зада­чу двумя заменами: первой - введем плоскость, которая перпенди­кулярна ABC, второй - плоскость, параллельную ABC.

Для того, чтобы построить плоскость П₄, перпендикулярную ABC, необходимо расположить ее так, чтобы она была перпенди­кулярна фронтали, либо горизонтали этого треугольника.

Пусть П₄ перпендикулярна горизонтали, тогда новая ось X₁₄ дол­жна быть перпендикулярна h₁ (рис. 1.56). Построим ее на произволь­ном расстоянии от А₁В₁С₁. Затем из точек А₁, В₁, С₁ проведем ли­нии связи перпендикулярно X₁₄. На каждой из них от оси X₁₄ отло­жим отрезок, равный расстоянию от фронтальной проекции соответствующей точки до оси Х₁₂. В результате получаем новую проекцию В₄А₄С₄ треугольника 

Рис. 1.56

ABC, которая представляет собой пря­мую, поскольку плоскость ABC перпендикулярна плоскости П₄.

Второй заменой вводим вместо П₁ плоскость П₅, параллельную плоскости треугольника ABC. Тогда получается система плоскостей проекций П₄/П₅, ось которой Х₄₅ параллельна B₄, A₄, C₄. Она может быть расположена на произвольном расстоянии от В₄А₄С₄. Далее из точек B₄, A₄, C₄ проводим линии связи перпендикулярно Х₄₅, и на каждой из них от оси Х₄₅ откладываем отрезок, равный расстоянию от гори­зонтальной проекции соответствующей точки до оси X₁₄. Получим точки А₅, В₅, С₅, соединив которые имеем А₅В₅С₅, который и явля­ется натуральной величиной ABC, поскольку в новой системе плос­костей проекций ABC параллелен плоскости П₅.

Определение натуральной величины двугранного угла. Для того чтобы решить задачу об определении натуральной величины двугранного угла, необходимо построить дополнитель­ную плоскость проекций, которая перпендикулярна ребру этого угла.

Одной заменой плоскостей эту задачу решить невозможно, так как дополнительная плоскость проекций должна быть перпендику­лярной не только ребру двугранного угла, но и одной из плоскостей проекций, о чем говорилось чуть выше. Поэтому необходимы две замены плоскостей проекций. Сначала вводим плоскость, парал­лельную ребру, а затем - перпендикулярную ему.

На комплексном чертеже (рис. 1.57) видно, что поскольку первая дополнительная плоскость проекций должна быть параллельна реб­ру АВ двугранного угла, то новая ось X₁₄ (П₁/П₄) должна быть парал­лельна либ

Рис. 1.57

о горизонтальной, либо фронтальной проекции ребра АВ. Пусть дополнительная плоскость П₄ параллельна АВ и перпендику­лярна плоскости П₁ тогда ось X₁₄ параллельна A₁В₁. Чтобы получить проекцию двугранного угла в плоскости П₄, необходимо каждую из точек А, В, С, D спроецировать на П₄.

Для этого из каждой точки A₁, В₁, С₁, D₁ проводим линию связи перпендикулярно оси X₁₄ и от этой оси откладываем отрезок, рав­ный расстоянию от фронтальной проекции точки до оси Х₁₂. Соеди­няя построенные точки A₄, В₄, С₄, D₄ соответствующим образом, по­лучаем проекцию двугранного угла в плоскости П₄.

Следующую ось Х₄₅ проводим перпендикулярно A₄В₄ так как плоскость П₅ должна быть перпендикулярна ребру АВ двухгранного угла. Проводим из точек A₄, В₄, С₄, D₄ линии связи перпендикулярно оси Х₄₅. Естественно, для точек A₄ и В₄ линия связи одна и та же. Теперь на линии связи, например для точки D, откладываем от оси Х₄₅ отрезок, равный расстоянию от D₁ до оси X₁₄, и получаем точку D₅. Аналогично получаем остальные точки. Поскольку A₁В₁ парал­лельна X₁₄, расстояние от A₁ и В₁ до оси X₁₄ одинаковое. Следователь­но, A_s = B_s. Полученный плоский угол α и есть натуральная величи­на двугранного утла.

Отметим очевидный факт, что натуральная величина любого геометрического объекта не меньше каждой из его проекций.

Определение кратчайшего расстояния от точки до прямой. Чтобы определить кратчайшее расстояние от точки до прямой, то есть длину перпендикуляра проведенного к прямой из заданной точки, необходимо построить плоскость проекций, параллельную этому перпендикуляру и перпендикулярную заданной прямой. Зна­чит, прямая должна по отношению к этой дополнительной плоско­сти проекции принять проецирующее положение и проецироваться на нее в точку. А это, в случае задания прямой общего положения возможно двумя заменами плоскостей проекций, как видно из реше­ния предыдущей задачи. (См. рис. 1

Рис. 1.58

.57)

Пусть требуется определить расстояние от точки С до прямой общего положения АВ. Приводим прямую в проецирующее положе­ние (рис. 1.58), аналогично построениям на рис. 1.57. Сначала строим ось X₁₄ параллельную А₁В₁, а затем ось Х₄₅ перпендикулярную A₄В₄. При этом А_А удалена от X₁₄ на то же расстояние, что и А₂ от оси X₁₂. В свою очередь, точка A_s удалена от Х₄₅, так же, как А₁ от оси X₁₄.

Поскольку точки A₅ и В₅ сливаются в одну, то длина отрезка C_5D5 есть кратчайшее расстояние между прямой АВ и точкой С.

Подобным образом решается задача на определение кратчайше­го расстояния между плоскостью общего положения и точкой, с той лишь разницей, что достаточно одной замены плоскостей проекций, чтобы привести плоскость в проецирующее положение. А перпендикуляр из заданной точки к прямой, в которую преобразуется заданная плоскость на новой плоскости проекций, и есть кратчайшее расстояние между плоскостью и точкой. Очевидно, если плоскость занимает частное положение в пространстве, тогда решение возмож­но без дополнительных построений на той плоскости проекций, к которой заданная плоскость перпендикулярна.

Определение кратчайшего расстояния между двумя скрещивающимися прямыми. Для решения этой задачи необходимо построить плоскость, па­раллельную перпендикуляру к обеим скрещивающимся прямым. Также эта дополнительная плоскость должна быть перпендикуляр­на одной из заданных прямых. Если прямые занимают общее поло­жение, тогда задача решается двумя заменами плоскостей проекций.

П

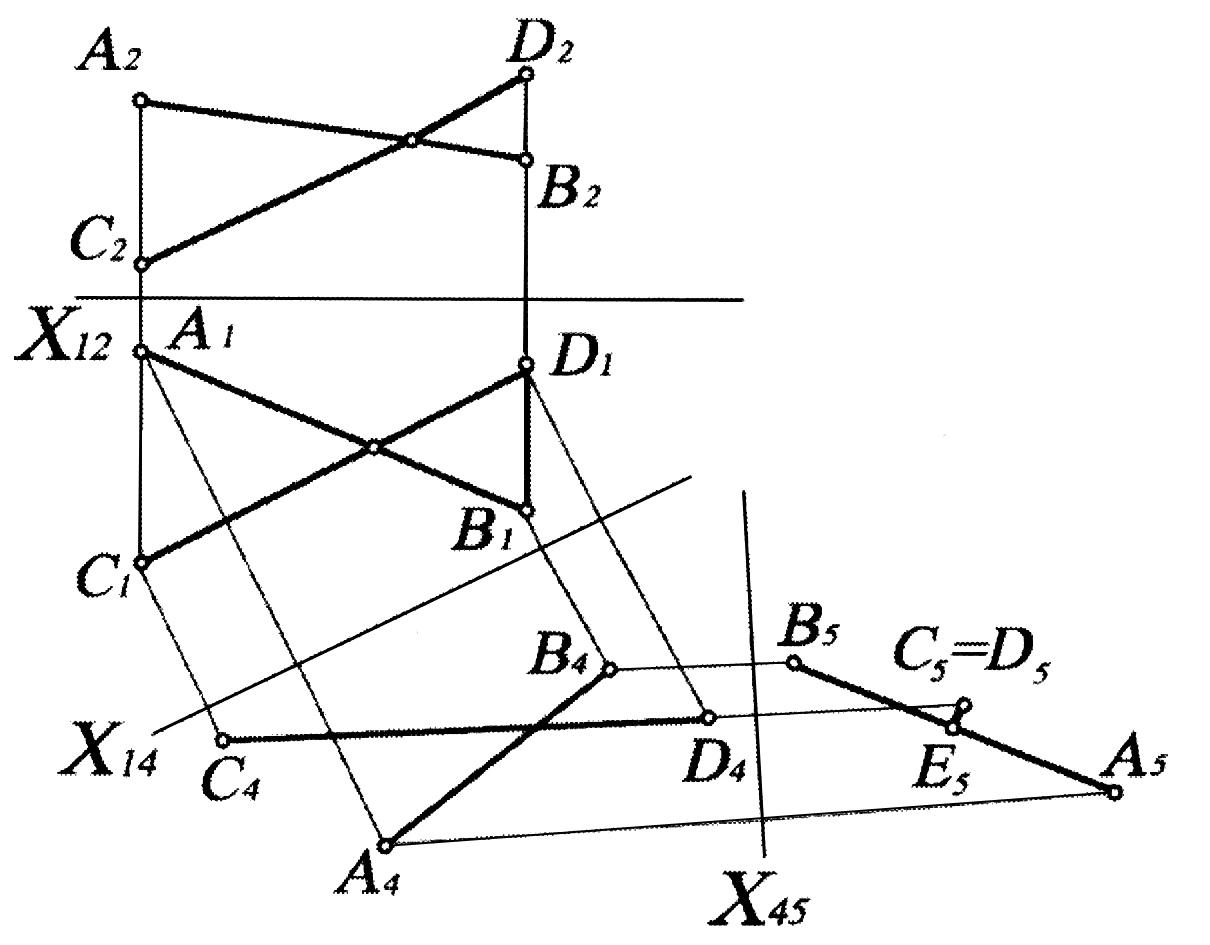Рис. 1.59

усть требуется определить кратчайшее расстояние между прямы­ми a и b. Необходимо каждую из них ограничить крайними точками A,В и CD .(Рис. 1.59)

Решение задачи сводится к приведению одной из прямых, на­пример CD, в проецирующее положение. Для этого первую допол­нительную плоскость П₄ располагаем параллельно CD и П₁, а вторую дополнительную плоскость П₅ - перпендику­лярно CD и П₄.

Все построения проекций точек А, В, С, D в плоскостях П₄ и П₅ аналогичны построениям в предыдущих задачах. Поскольку на П₅ проекции С₅ и D_s совпадают, т. е. CD является проецирующей по отношению к П₅, то кратчайшим расстоянием между прямыми а и b будет длина отрезка прямой С₅Е₅, который представляет собой перпендикуляр к A₅В₅ проведенный из точки С₅.

Следует отметить, что решение задачи упрощается, если одна из заданных прямых занимает частное положение.

Задача о нахождении кратчайшего расстояния между двумя па­раллельными прямыми решается аналогично сначала строим но­вую плоскость проекций параллельно заданным прямым, а затем перпендикулярно к ним. Тогда после второй замены плоскостей про­екций заданные прямые будут спроецированы в точки, и длина пря­мой, соединяющей эти точки, будет представлять собой кратчайшее расстояние между параллельными прямыми.

Таким образом, способ замены плоскостей проекций, позволя­ющий решать широкий спектр задач, является наиболее универсаль­ным и распространенным, сочетающим наглядность с простотой построений.

Поворот плоскости вокруг ее следа до совмещения с соответ­ствующей плоскостью проекций. Этот способ является случаем вращения вокруг горизонтали или фронтали, так как горизонтальный след плоскости можно рассматривать как «нулевую» горизонталь горизонтальной плоскости, а фрон­тальный след - как «нулевую» фронталь.

Каждый из следов плоскости является осью вращения, и, следовательно, все точки вращае­мой плоскости описывают окружности в пло­скостях, перпендикулярных к следу, вокруг которого происходит вращение.

В результате вращения плоскости вокруг горизонтального следа — горизонтали — все точки совмещаемой плоскости совместятся с го­ризонтальной плоскостью проекций, а в резуль­тате вращения плоскости вокруг фронталь­ного следа — фронтали все точки плоскости совместятся с фронтальной плоскостью проек­ций. Такое действие называют совмещением.

1. Совмещение плоскости общего положения α с плоскостью П₁. На рисунке 1.60, а показано наглядное изображение поворота плоскости общего положения вокруг горизонтального следа в направлении от плоскости к зрителю до совмещения с плос­костью П₁.

Для решения этой задачи надо совместить любую точку следа l с пло­скостью П₁ например точку А (см. рис. 1.60, а). След k является осью вращения. Точка F схода следов лежит на оси вращения и не из­менит своего положения.

Вводим плоскость вращения  для точки А, перпендикулярную к следу k; она будет гори­зонтально-проектирующей и пересечет след k в точке О — центре вращения.

Р

Рис. 1.60

адиусом вращения является отрезок ОА — линия пересечения плоскостей α и .

Точка А при вращении опишет в плоскости  дугу и на проекции ₁ определит место совме­щенной точки А₁, через кото­рую из точки F должен про­ходить совмещенный след l₁.

Рассмотрим выполнение на комплексном чертеже совмеще­ние следа l с плоскостью П₁. (Рис. 1.60, б).

На следе l берут произволь­ную точку А (А₁, А₂). Затем через проекцию А₁ этой точки проводят проекцию ₁ горизон­тально-проецирующей плоско­сти  перпендикулярно к про­екции k ₁ следа k, который при­нят за ось вращения.

Так как отрезок A₂F₁₂ при вращении плоскости не изменит своей величины, то точку А₁* можно получить как пересече­ние проекции ₁ с дугой, про­веденной из центра F₁₂ радиу­сом F₁₂A₂.

Прямая, проведенная из точки F₁₂ через точку А₁* является следом l₁*, совмещенным с пло­скостью П₁, что и определяет совмещение плоскости α с пло­скостью П₁.

В случае совмещения данной плоскости с плоскостью проекций П₂ следует в качестве плоскости вращения брать фронтально-проецирующую плоскость, перпендикулярную к следу l .

Совмещение точки, принадлежащей плос­кости общего положения, с плоскостями про­екций. Требуется совместить плоскость общего положения β, заданную проекциями k₂ и l₂ ее следов, с находящейся на ней точкой А с плоскостью проекций П₁. (Рис. 1.60, в). Для решения данной задачи воспользуемся горизонталью. Проведем через заданную точку А горизон­таль h, совместим ее и след l с плоскостью П₁ при помощи точки N (следа горизонтали), одновременно принадлежащей как горизонтали, так и следу l. Получим проекцию N₁* совмещенной точки N и проекцию l₁* совмещенного следа l.

Зная, что горизонтальные проекции горизон­талей параллельны следу плоскости, в которой они лежат, проводим из точки N₁* прямую па­раллельно следу k₁, получаем совмещенную горизонталь и на ней проведением из точки А₁ прямой, перпендикулярной к следу k₁, определяем место совмещенной точки А. Точка пересечения этой прямой с совмещенной горизон­талью является искомой совмещенной проек­цией А₁*.

При определении длины отрезка прямой, лежащего в плоскости общего положения, до­статочно совмещения его крайних точек с одной из плоскостей проекций, а при определении формы и размеров фигуры — совмещения ее вершин.

На Рис. 1.60, г приведен пример определения формы и размеров треугольника при помощи горизонталей, проведенных через его вер­шины.