1.3. Проекция прямой.

Следующим после точки геометрическим объектом, проециро­вание которого рассматривается, является прямая линия. Посколь­ку ее положение в пространстве однозначно определяется двумя точками, то и для определения положения проекций прямой также достаточно зафиксировать проекции двух точек. Поэтому для построения проекций прямой можно использовать все правила, касающиеся про­ецирования точки.

Прямые частного и общего положения. Прямая называется прямой частного положения, если она зани­мает в пространстве частное положение, а именно либо параллель­на, либо перпендикулярна одной из плоскостей проекций. Для об­легчения усвоения основных понятий рассмотрим проецирование прямых, расположенных в первой четверти.

П

Рис. 1.11

рямые уровня. Прямой уровня называется прямая, параллельная одной из плос­костей проекций. Поскольку плоскостей проекций три, то и прямых уровня тоже три.

1. Прямая, параллельная горизонтальной плоскости проекций П₁, называется горизонтальной прямой уровня или горизонталью и обо­значается h. (Рис. 1.11, а, б)

2. Прямая, параллельная фронтальной плоскости проекций П₂, называется фронтальной прямой уровня или фронталью и обозна­чается f.

3. Прямая, параллельная профильной плоскости проекций П₃, на­зывается профильной прямой уровня и обозначается p.

Исходя из положения прямых уровня в пространстве, фронтальные и профильные проекции выглядят так, как показано на рис. 1.11, в, г.

Горизонталь характерна тем, что ее фронтальная проекция па­раллельна оси ОХ. Фронталь характерна тем, что ее горизонтальная проекция параллельна оси ОХ. При этом по правилу взаимосвязи проекций расстояние от f₃ до оси OZ равно расстоянию oт f₁ до оси ОХ. У профильной линии уровня и фронтальная и горизонтальная проекции перпендикулярны оси ОХ.

Очевидно, что если прямая параллельна какой-либо плоскости, то на эту плоскость она проецируется в натуральную величину (без ис­кажений). Поэтому h_1, f_2, p₃ - это натуральная величина соответствую­щих прямых h, f, p, α - угол наклона прямой уровня к П₂; β - угол наклона прямой уровня к П₂; γ - угол наклона прямой уровня к П₃.

П

Рис. 1.12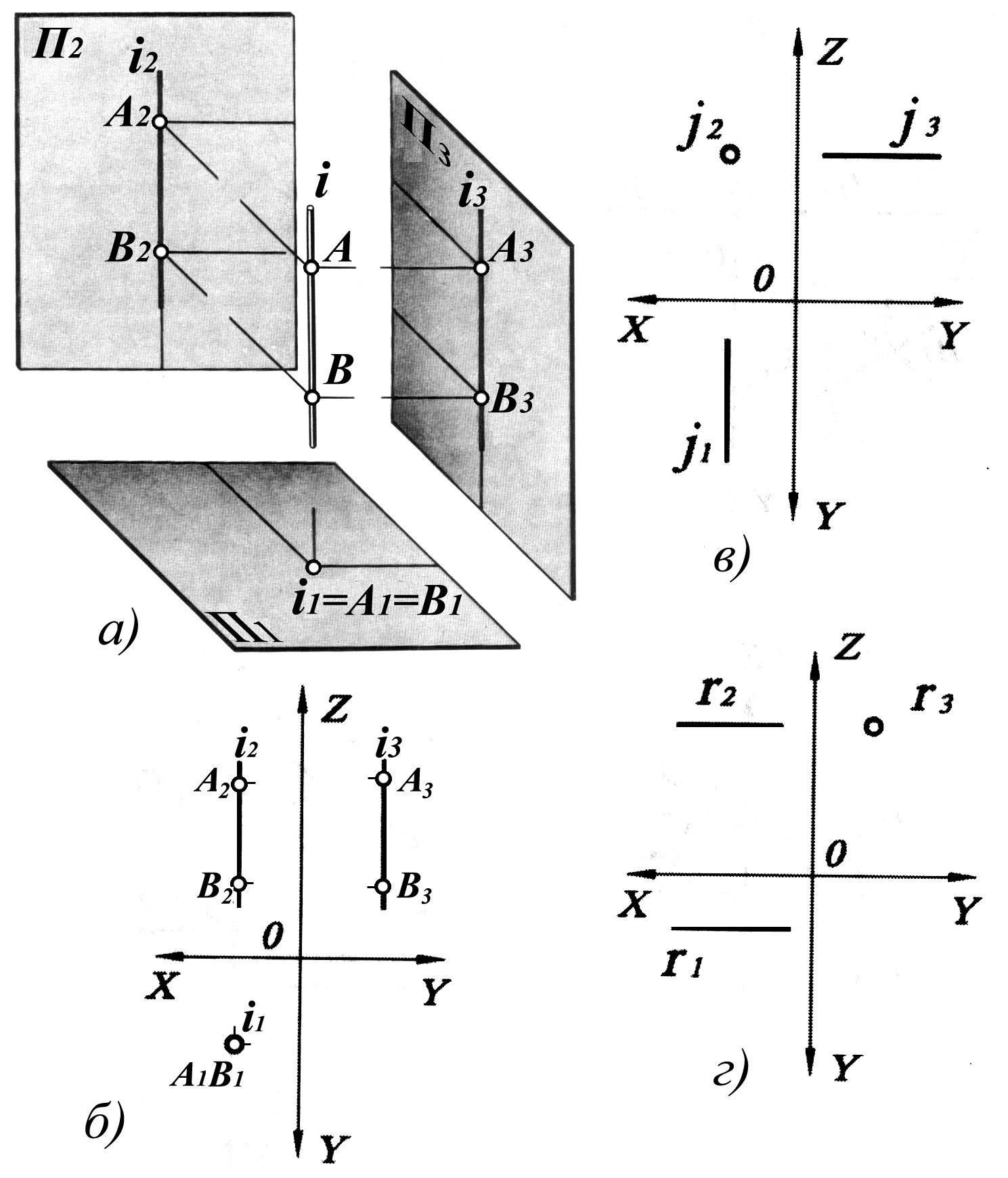

роецирующие прямые. Проецирующей прямой называется прямая, перпендикулярная одной из плоскостей проекций, а, следовательно, параллельная двум другим плоскостям проекций.

1. Прямая, перпендикулярная горизонтальной плоскости проек­ций П₁ называется горизонтально-проецирующей прямой и обозна­чается i. (Рис. 1.12, а, б)

2. Прямая, перпендикулярная фронтальной плоскости проекций П₂, называется фронтально-проецирующей прямой и обозначается j. (Рис. 1.12, в)

3. Прямая, перпендикулярная профильной плоскости проекций П₃, называется профильно-проецирующей прямой и обозначается r. (Рис. 1.12, г)

Горизонтально-проецирующая прямая характерна тем, что ее го­ризонтальной проекцией является точка, а фронтальная проекция перпендикулярна оси ОХ. Фронтально-проецирующая прямая характерна тем, что ее фронтальной проекцией является точка, горизонтальная проекция перпендикулярна оси ОХ. У профильно-проеци­рующей прямой фронтальная и горизонтальная проекции параллель­ны оси ОХ, а профильная проекция – точка.

У проецирующих прямых две проекции параллельны плоскостям проекций. Поэтому i₂, i₃, j₁, j₃, r₁, r₂ - это натуральные величины со­ответствующих прямых i, j, r.

П

Рис. 1.13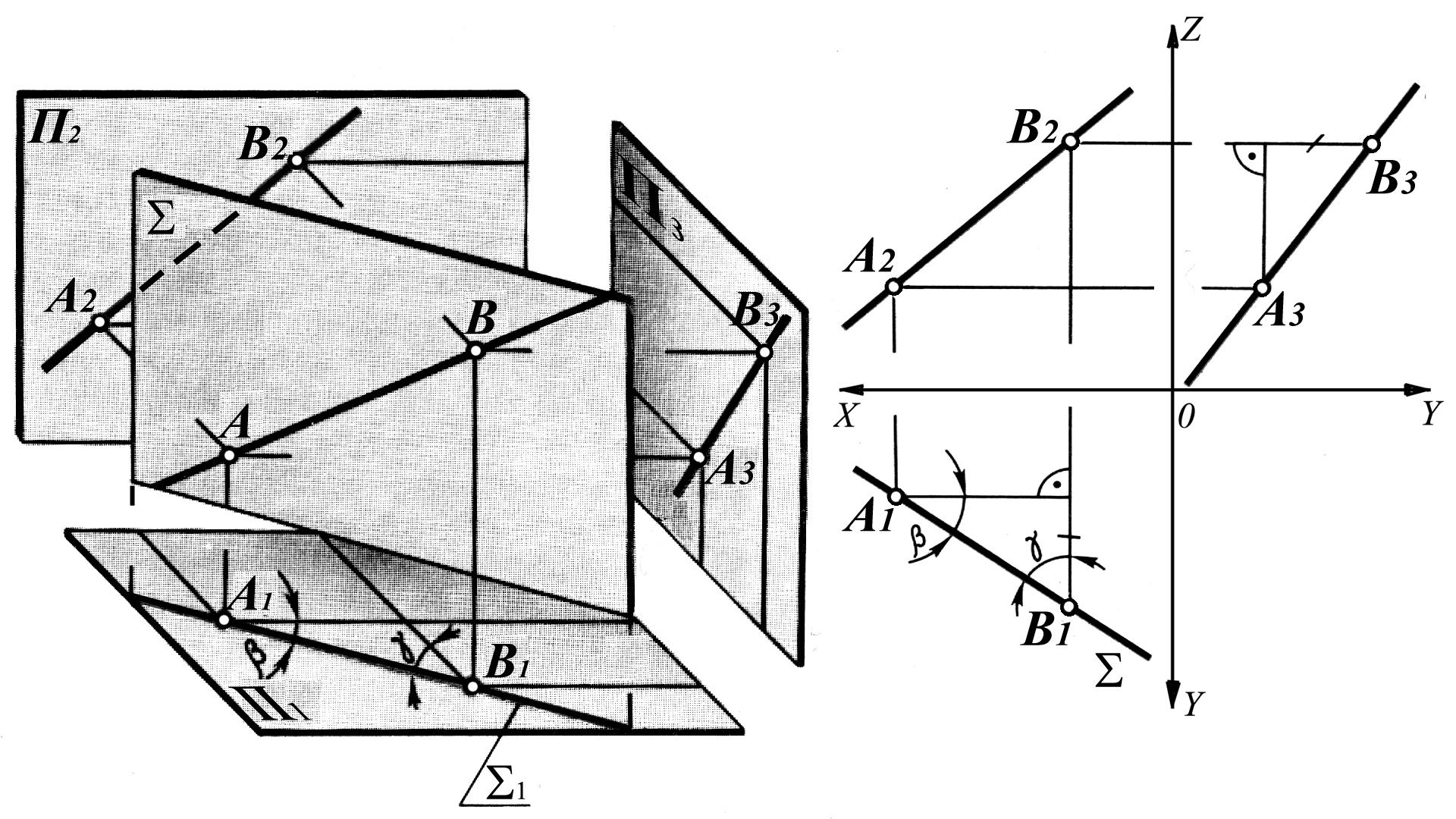

рямая общего положения. Прямой общего положения называется прямая, занимающая об­щее положение в пространстве, т. е. не параллельная ни одной из плоскостей проекций, а следовательно, расположенная к каждой из них под углом.

Естественно, что ни одна из проекций прямой общего положе­ния не показывает ее натуральную величину, а также угол наклона к одной из плоскостей проекций. (Рис. 1.13) Любая проекция такой пря­мой меньше самой прямой. Таким образом, для прямой общего положения верно утверждение натуральная величина больше или равна любой ее проекции.

Проецирование прямой, расположенной во II четверти (вII) изображено на рис. 1.14.

Деление отрезка прямой в заданном отношении. При делении отрезка прямой в заданном отношении используется теорема о подобии треугольников, известная из курса элементарной геометрии. Так, если необходимо отрезок АВ разделить в отношении 2 : 3, тогда и его проекции будут разделены в том же отношении. Для этого на одной из проекц

Рис. 1.14

Рис. 1.15

ий (например, горизонтальной) из любой граничной точки (например, В) отрезка проведем прямую линию d в произволь­ном направлении. (Рис. 1.15) Затем отложим на ней 5 равных отрезков, после чего соединим полученную точку В* с точкой А₁. Далее, через вторую засечку на линии d проведем прямую, параллельную А₁В*. На отрезке А₁В₁ получим точку С₁, которая делит его в заданном отноше­нии, т. е. В₁ С₁ : А₁ С₁=2:3.

Проведя соответствую­щие линии проекционной с вязи, получим точки деления на проекциях А₂В₂ и А₃В_3. Таким образом, разделив проекции отрезка в заданном отношении, мы тем самым решили задачу деления самого отрезка.

Определение натуральной величины отрезка прямой и углов наклона его к плоскостям проекций методом прямоугольного треугольника. Одним из методов определения натуральной величины отрезка прямой является метод прямоугольного треугольника, который мож­но сформулировать так натуральной величиной отрезка является гипотенуза прямоугольного треугольника, одним из катетов которо­го служит горизонтальная (фронтальная) проекция отрезка, другим - разность расстояний от граничных точек фронтальной (горизон­тальной) проекции отрезка до оси ОХ. При этом углом наклона от­резка к горизонтальной (фронтальной) плоскости проекции являет­ся угол между гипотенузой прямоугольного треугольника и гори­зонтальной (фронтальной) проекцией отрезка.

К

Рис. 1.16

ак видно из рис. 1.16, а длину отрезка прямой АВ можно определить из прямоугольного треугольника АВ*В, в котором: катет АВ* =А₁В₁ (проекции отрезка АВ на плоскость П₁), а катет ВВ* равен ∆z — разности расстояний точек А и В от плоскости П_1. Угол φ в том же треугольнике определяет угол наклона отрезка прямой АВ к плоскости П_1. (Рис. 1.16, б)

Если вместо плоскости П₁ взять плос­кость П₂, то длину отрезка АВ можно определить аналогичным путем из прямоу­гольного треугольника ABA* (рис. 1.16, в), где катет ВА* равен проекции А₂В₂, а второй катет АА* равен ∆y — разности расстоя­ний точек А и В от плоскости П₂. Угол ψ в том же треугольнике ABA* определяет угол наклона прямой АВ к плоскости П₂.

На рис. Рис. 1.16, б, в показано на эпюрах нахождение длины отрезка прямой и углов наклона его к плоскостям П₁ (угол φ) и П₂ (угол ψ).

В

Рис. 1.17

заимное положение прямых в пространстве. Конкурирующие точки. Видимость.

Прямые в пространстве могут занимать по отношению друг к другу одно из трех положений: рис. 1.17, а - быть параллельными, рис. 1.17, в - пересекаться, рис. 1.18, а - скрещиваться, т. е. не пересекаться, но и не быть параллельными. Рассмотрим, как располагаются их проекции. (Рис. 1.17, б, г, рис. 1.18, в)

В

Рис. 1.18

соответствии с одним из свойств ортогонального проецирова­ния, если прямые параллельны, то их одноименные проекции парал­лельны. (Рис. 1.17, а) Если прямые пересекаются, то их проекции пере­секаются, причем точки пересечения проекций лежат на одной линии проекционной связи (А - точка пересечения прямых с и d). (Рис. 1.17, в) Если пря­мые скрещиваются, то их проекции пересекаются, но точки пересече­ния проекций не лежат на одной линии проекционной связи (см. на рис. 1.18, а точки C₁ и В₂). Тогда, следуя по вертикальной линии связи от точки C₁, получим на каждой из прямых n₂ и m₂ соответственно две проекции точки - С₂ и некоторой точки D₂, а следовательно, на пере­сечении n₁ и m₁, лежат две точки С₁ и D₁, слившиеся в одну.

Точки, лежащие на одном проецирующем луче, называются кон­курирующими. Такие точки могут быть только на скрещивающихся прямых, что очевидно из их пространственного положения. Точки, горизонтальные проекции которых совпадают, называются горизон­тально-конкурирующими (см. рис 1.18, б, точки С и D), а если совпа­дают фронтальные проекции, то точки называются фронтально-кон­курирующими (см. рис. 1.18, б, точки В и Е).

При этом конкурирующие точки расположены на разном рассто­янии от плоскостей проекций. Фронтально-конкурирующая точка, расположенная ближе к П₂, будет закрыта от наблюдателя точкой, расположенной дальше от П₂, а следовательно, ближе к наблюдате­лю. Значит, ее горизонтальная проекция расположена дальше от ОХ. Тогда в нашем примере точка Е - видимая, а точка В – невидимая. Аналогично С - видимая, a D – невидимая. Таким образом, видимой является точка, у которой проекция расположена дальше от оси ОХ. Чтобы различать точки на чертеже, невидимую заключают в круг­лые скобки.

Следы прямой. Прямая общего положения пересекает все основные плоскости проекций. Точку пересечения прямой с плоскостью проекций назы­вают следом прямой.

В зависимости от того, с какой плоскостью проекций пересека­ется прямая, ее следы обозначаются следующим образом: M - гори­зонтальный след прямой, N – фронтальный. Соответствующие про­екции следов прямой обозначаются M₁ - горизонтальная проекция горизонтального следа, M₂ его фронтальная проекция. Отметим, что проекция M₁, совпа­дает с самим горизонтальным следом M, а его фронтальная проек­ция M₂ лежит на оси ОХ. Фронтальный след N совпадает с N₂ (фронтальной проекцией фронтального следа), а его горизонтальная проекция N₁, лежит на оси ОХ.

Д

Рис. 1.19

ля произвольного отрезка прямой АВ общего положения построим следы. (Рис. 1.19)

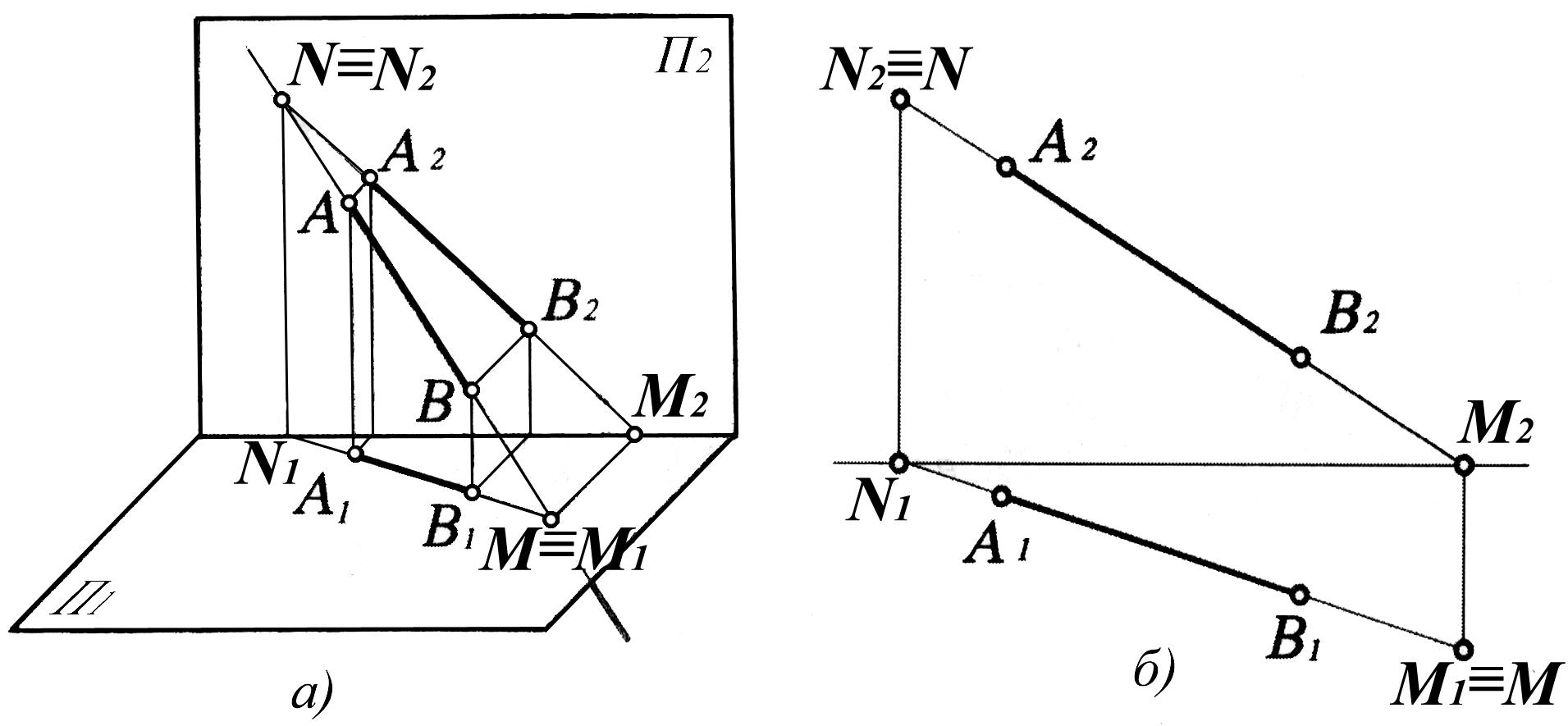
Чтобы найти горизонтальный след прямой, нужно продолжить фронтальную проекцию А₂В₂ до пересечения с осью ОХ. Полученная точка M₂ является фронтальной проекцией горизонтального следа. Из полученной точки проводим перпендикуляр к оси ОХ до пе­ресечения с продолжением горизонтальной проекции отрезка А₁В₁. Точка M₁ — горизонтальная проекция горизонтального следа, она со­впадает с самим горизонтальным следом.

Для нахождения фронтального следа продолжаем горизонтальную проекцию отрезка А₁В₁, до пересечения с осью ОХ через N₁ (го­ризонтальную проекцию фронтального следа) проводим перпенди­куляр до пересечения с фронтальной проекцией А₂В₂. Точка N₂ - фронтальная проекция фронтального следа, она совпадает с фронтальным следом N.

В

Рис. 1.20

заимно перпендикулярные прямые. Если две прямые пересекаются под прямым углом, то проекции их в общем случае образуют угол, не равный 90°.

Для того чтобы прямой угол проециро­вался в истинную величину, необходимо и достаточно, чтобы одна из его сторон была параллельна, а другая не перпенди­кулярна плоскости проекций.

Рассмотрим изображение на рис. 1.20, а пусть сторона АВ пря­мого угла ABC параллельна плоскости П₁. Докажем, что проекция его угол A_lB_lC_l = 90°.

Прямая АВ перпендикулярна плоскости α, так как АВ перпендикулярна двум пря­мым этой плоскости ВС и ВВ₁, проходя­щим через точку В.

Прямая АВ и ее проекция А₁В₁ — две параллельные прямые, а потому А₁В₁ так­же перпендикулярна плоскости α. Следо­вательно, А₁В₁перпендикулярна В₁С₁.

Докажем теперь, что если ортогональ­ная проекция угла ABC на некоторую плоскость П_1, является прямым углом и од­на из сторон угла параллельна той же плоскости, то угол ABC — прямой (рис. 1.20, а).

Прямая А₁В₁ перпендикулярна плоско­сти α, так как образует прямые углы с В₁С₁ по условию и с ВВ₁ по построению. Но А₁В₁ параллельна АВ. Значит, и пря­мая АВα. Следовательно, угол между АВ и ВС — прямой.

На основании изложенного можно ут­верждать, что углы, показанные на рис. 1.20, б, в, являются проекциями прямых углов. У первого из них сторона а параллельна плоскости П₁ у второго — сторона f па­раллельна плоскости П₂.