§ 12.7 Элементы комбинаторики

Определение Произвольное подмножество из множества называется выборкой объема .

Определение Выборка называется упорядоченной (неупорядочен ной), если порядок следования элементов в ней существенен (не суще ственен).

Определение Упорядоченная выборки объема из элементов называется - размещением.

ЗАМЕЧАНИЕ Количество всевозможных -размещений

вычисляется по формуле .

Определение Упорядоченная выборка объема из набора

элементов называется перестановкой.

ЗАМЕЧАНИЕ Число всевозможных перестановок в группе из элементов вычисляется по формуле .

Определение Неупорядоченная выборка объема называется

- сочетанием.

ЗАМЕЧАНИЕ 1 Число сочетаний из во множестве из

элементов вычисляется по формуле .

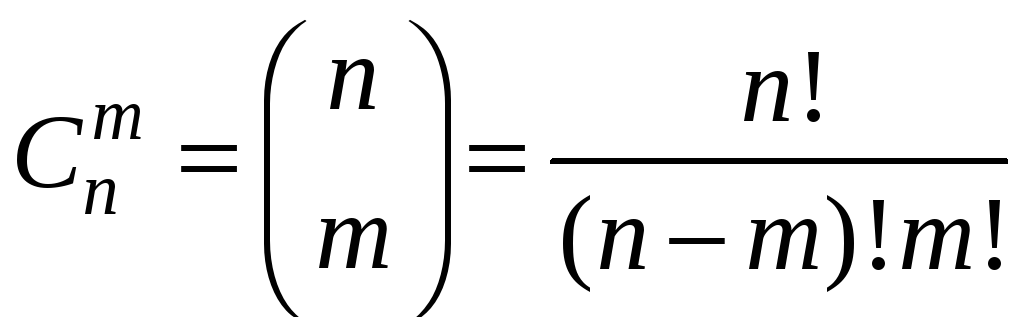ЗАМЕЧАНИЕ 2 Число всевозможных разбиений множества из

элементов на подмножеств объемов соответственно

вычисляется по формуле .

◄ Число всевозможных неупорядоченных выборок объема вычисляется по формуле . На втором шаге из оставшихся элементов можно произвести неупорядоченных выборок объема . И так далее. На последнем шаге из оставшихся элементов можно организовать неупорядоченных выборок объема . Искомое число всевозможных разбиений тогда равно

. ►

СЛЕДСТВИЕ 1 (обобщенная формула бинома Ньютона для

слагаемых) .

_____

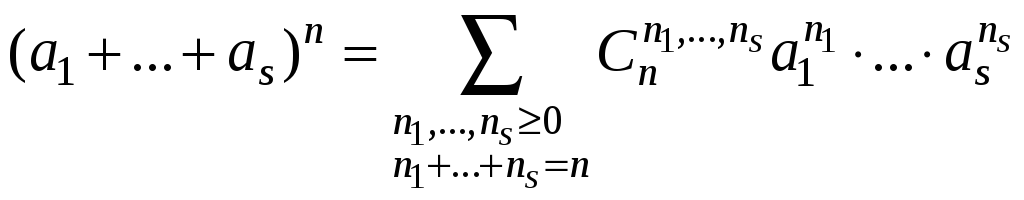ЗАМЕЧАНИЕ 1 (правило суммы) Пусть есть

подмножества множества . Обозначим число элементов

(длину, площадь) множества . Тогда

.

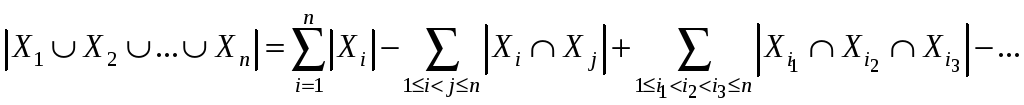
◄ Обоснуем замечание при .

.

Теперь воспользуемся этой формулой.

. ►

ЗАМЕЧАНИЕ 2 (правило произведения) Если множества

конечны, то число элементов декартова произведения

конечно и вычисляется по формуле

.