
- •Наземная фотограмметрия
- •7.1 Области применения наземной фотограмметрии
- •7.2 Съемочные камеры, применяемые в наземной фотограмметрии
- •7.3 Фотограмметрическая калибровка цифровых съемочных камер
- •7.3.1 Калибровка цифровых фотокамер по снимкам пространственного тест-объекта.
- •В которых:
- •В которых:
- •7.3.2 Калибровка цифровых фотокамер по снимкам плоского тест-объекта.
- •7.3 Системы координат, применяемые в наземной фотограмметрии и элементы ориентирования наземных снимков.
- •7.4 Основные случаи наземной стереофотограмметрической съемки
- •7.5 Точность наземной стереофотограмметрической съемки.
- •7.6 Особенности фотограмметрической обработки наземных снимков
- •7.8 Особенности наземной фотограмметрической съемки инженерных конструкций и сооружений
В которых:
f – фокусное расстояние съемочной камеры;
xo, yo – координаты главной точки в системе координат снимка;
x, y – координаты изображения точки тест-объекта в системе координат снимка;
X, Y, Z - координаты соответствующей точки тест-объекта в системе координат объекта;
XS, YS, ZS – координаты точки фотографирования (центра проекции);
aij – элементы матрицы преобразования координат (направляющие косинусы), являющиеся функциями угловых элементов внешнего ориентирования съемочной камеры , , ;
dx, dy – поправки в измеренные на снимке координаты x, y изображения точки тест-объекта за дисторсию объектива, определяемые уравнениями (7.1).
Полученную по всем измеренным на снимке изображениям точек тест-объекта систему уравнений решают методом приближений по способу наименьших квадратов. В результате решения системы уравнений определяют элементы внешнего ориентирования снимка XS,YS,ZS, ,, и параметры внутреннего ориентирования снимка f, xo, yo, k1, k2, k3, p1, p2 с оценкой точности их определения.
При решении исходные уравнения приводят к линейному виду, раскладывая их в ряд Тейлора с сохранением членов только первого порядка малости, и переходят к уравнениям поправок вида:
![]() , (7.3)
, (7.3)
В которых:
B – матрица коэффициентов уравнений поправок (частные производные от исходных уравнений по неизвестным) размерностью m x n (m – число уравнений, n – число неизвестных);
δ – матрица поправок к элементам внешнего ориентирования снимка и параметрам внутреннего ориентирования матрица размерностью 1 x n;
L – матрица свободных членов размерностью 1 x m;
V - матрица поправок в измеренные координаты точек снимка размерностью 1 x m.
В нашем случае m = 2k, где k – число точек тест-объекта, измеренных на снимке, а n = 14.
 ;
;
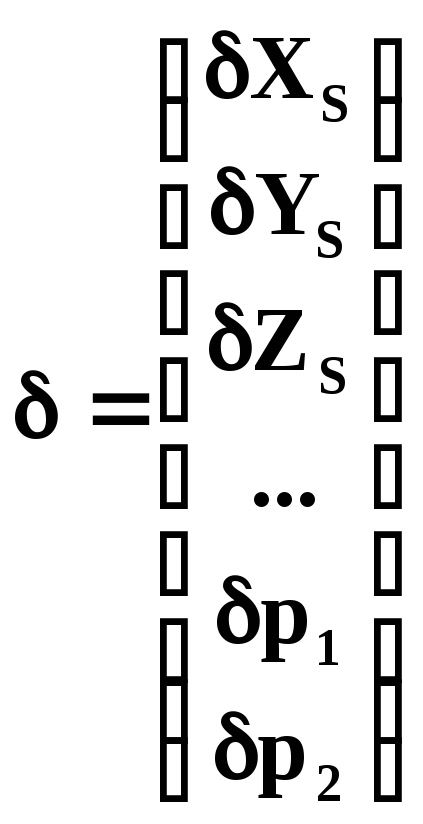 ;
;
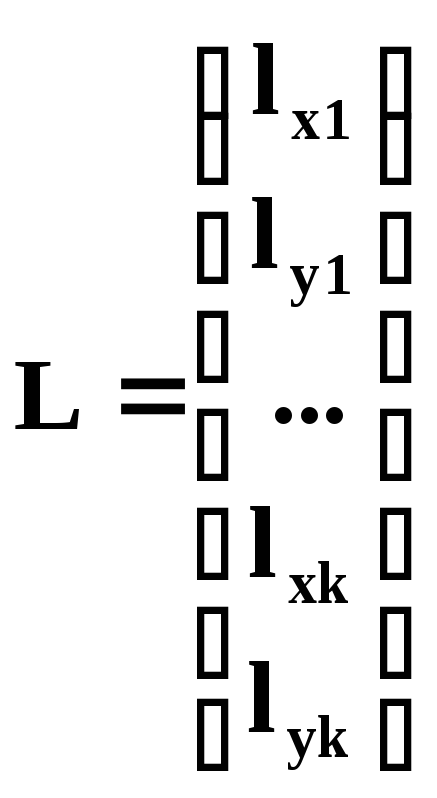 ;
;
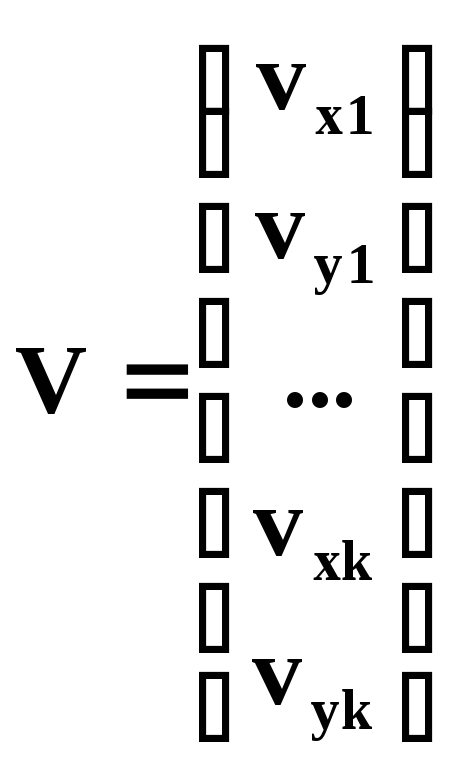
Значения коэффициентов уравнений поправок (7.3) ai, bi вычисляются по известным значениям координат х, у изображений точек тест-объекта измеренных на снимке, координат точек тест-объекта X, Y, Z и приближенным значениям элементов внешнего ориентирования снимка XS, YS, ZS, , , и элементов внутреннего ориентирования снимка f, xo, yo, k1, k2, k3, p1, p2.
Свободные члены ℓх, ℓу вычисляются по формулам (7.2) таким же образом.
Для решения системы линейных уравнений (7.3) по способу наименьших квадратов переходят к нормальным уравнениям:
![]()
или
![]() , (7.4)
, (7.4)
где N - матрица коэффициентов нормальных уравнений размерностью n x n; LN – матрица размерностью 1 x n свободных членов нормальных уравнений; P – диагональная матрица весов измерений:
 .
.
Pi = 1/ mi2
mi – средняя квадратическая ошибка i-го измерения.
В результате решения уравнений (7.4) получим:
![]()
или
![]() . (7.5)
. (7.5)
Здесь Q - обратная матрица коэффициентов нормальных уравнений.
Таким образом, получают поправки ко всем приближенным значениям неизвестных элементов внешнего ориентирования снимка и параметрам внутреннего ориентирования камеры и вычисляют уточненные их значения:
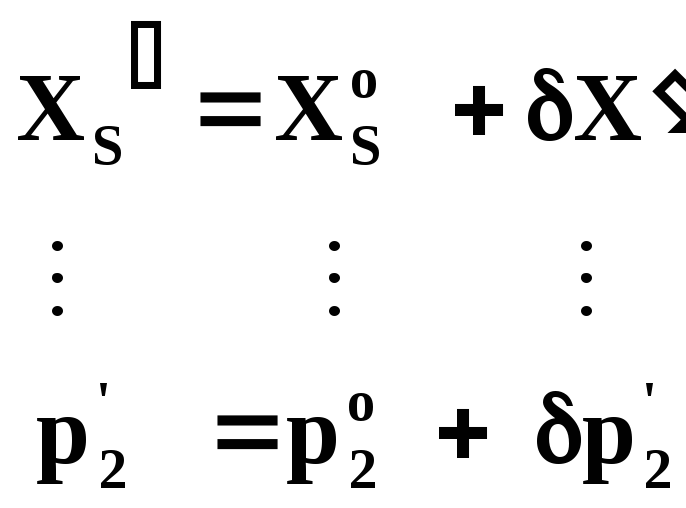
По уточненным значениям неизвестных снова составляют уравнения поправок (7.3) и решают полученную систему уравнений по способу наименьших квадратов. Так продолжают до тех пор, пока поправки к неизвестным станут пренебрегаемо малыми величинами. В результате получают уравненные значения элементов внешнего ориентирования снимка и параметры внутреннего ориентирования камеры. В последнем приближении выполняют оценку точности определения неизвестных, т.е. вычисляют средние квадратические ошибки неизвестных:
![]() (7.6)
(7.6)
![]() (7.7)
(7.7)
μ – средняя квадратическая ошибка единицы веса, Qjj – диагональные элементы обратной матрицы; m-n - число избыточных измерений.
При определении параметров фотограмметрической калибровки по методике изложенной выше, необходимо с достаточно высокой точностью знать приближенные значения элементов внутреннего и внешнего ориентирования съемочной камеры. Их значения определяют прямым методом, используя уравнения проективных преобразований координат соответственных точек снимка и объекта.
Эти уравнения имеют вид
![]()
(7.8)
![]()
В уравнениях (7.8):
x, y – координаты точки на снимке;
X, Y, Z – координаты соответственной точки объекта;
L1,…,L11 – коэффициенты проективных преобразований.
Уравнения (7.8) после преобразований можно представить в виде
L1 X + L2 Y + L3 Z + L4 – xX L9 – xY L10 – xZ L11 - x = 0
(7.9)
L5 X + L6 Y + L7 Z + L8 – yX L9 – yY L10 – yZ L11 - y = 0
Каждое изображение опорной точки, измеренное на снимке, позволяет составить два уравнения с одиннадцатью неизвестными. Для нахождения значений коэффициентов L1,…,L11 необходимо измерить на снимке координаты изображений не менее шести опорных точек, из которых, по крайней мере, одна не должна лежать с остальными в одной плоскости. Полученную систему линейных уравнений (7.9) решают по методу наименьших квадратов и находят значения коэффициентов проективных преобразований L1,…,L11.
По значениям коэффициентов проективных преобразований можно вычислить элементы внутреннего и внешнего ориентирования снимка по следующим формулам:
xo = (L1 L9 + L2 L10 + L3 L11) L2
yo = (L5 L9 + L6 L10 + L7 L11) L2
f = ( fx + fy ) / 2
![]()
![]()
(7.10)
α = sin-1 (L9 L)
= tg-1 (-L10/L11)
= cos-1 (L ( xo L9 - L1)) / fx ) / cosα
![]()
В уравнениях (7.10)
![]()
Полученные по формулам (7.10) значения элементов внутреннего и внешнего ориентирования используют в качестве начальных приближений при составлении уравнений поправок (7.3).
С целью повышения надежности и точности определения параметров внутреннего ориентирования калибруемых камер, целесообразно производить съемку тест-объекта многократно с поворотом камеры вокруг оптической оси объектива на 180о и определять искомые параметры в результате совместной обработки измерений выполненных по всем полученным снимкам.
Критерием оценки точности проведенной фотограмметрической калибровки цифровой камеры и, как следствие, критерием пригодности камеры для выполнения фотограмметрических определений являются значения остаточных погрешностей координат измеренных на снимке точек. Их значения в зависимости от типа калибруемой съемочной камеры должны лежать в пределах от 0.15 до 0.5 пикселя.
На рис. 7.11 и 7.12 представлены образцы сертификатов калибровки цифровой фотокамеры. В первом сертификате за единицу измерений был принят пиксель, а во втором миллиметр.


