3. Статистична перевірка моделі залежності

Коректність побудови регресійної моделі залежності перевіряється найчастіше за допомогою наступних характеристик:

1) показників мультиколінеарності між факторами з правої частини рівняння (10). Повна кореляція між двома такими факторами знеможливлює обчислення параметрів методом найменших квадратів. Часткова мультиколінеарність веде до збільшення стандартних помилок параметрів, і отже, до зниження ефективності оцінок [2];

2) стандартних помилок параметрів (коефіцієнтів) у моделі;

3) стандартної помилки рівняння;

4) коефіцієнта детермінації (або кореляції) для моделі;

5) автокореляції залишку . Чим більше автокореляція залишку, тим більше впевненості в тому, що існує деякий неврахований фактор, що пояснює зміну ендогенної перемінної Y і тим нижче ефективність оцінювання за методом найменших квадратів [2].

а) Покажемо, що для обраних залежностей (2) - (7) фактори не мультиколінеарні, тобто .

З (14) випливає, що - матриця системи нормальних рівнянь. (15) - (20) для цих залежностей.

Наприклад, для (17)

(21)

(22)

Аналогічно цей факт доводиться для інших систем нормальних рівнянь.

б) Після виключення з моделі перемінних (факторів) , що призводять до мультиколінеарності, тобто виключення , вирішується система нормальних рівнянь для визначення оцінок параметрів обраної моделі залежності. Статистичну значимість знайдених коефіцієнтів регресійного рівняння оцінюють за допомогою стандартних помилок параметрів.

Коваріаційна матриця параметрів , , визначається співвідношенням

, (23)

де - стандартна помилка обраної моделі залежності, обчислена з обліком ступенів свободи, тобто числа факторів у моделі. Як береться .

Матриця має розмірність , тому, що, крім дисперсій, оцінок впливу факторів x_i(t) (i=1; 2; . . .; m), b_i, вона містить дисперсію постійного члена b₀.

Стандартна помилка параметра , дорівнює квадратному кореню з i-го діагонального елемента матриці , тобто

(24)

Статистична значимість перевіряється за допомогою t-критерію в припущенні, що E(t) розподілені за нормальним законом. Для перевірки обчислюються розрахункові значення критерію для оцінок b_i, (i=1; 2; 3; . . . ; m) (25)

Якщо , де - табличне значення критерію для рівня значимості і числа ступенів свободи v = n-m-1, то оцінка параметра b_i, , значимо відрізняється від нуля, тобто вплив фактора на Y значимо.

При - вплив чинника не значущий, і він виключається з моделі. У цьому випадку оцінювання параметрів повторюється вже для нової моделі, без врахування впливу цього фактора, тобто знову складається і вирішується система нормальних рівнянь, але менша на число виключених із моделі факторів . Для знову отриманих оцінок роблять перевірку їхньої значимості. Якщо вони всі значимі, то модель залежності вважається отриманою, у противному випадку знову повторюється процедура виключення факторів із моделі і перерахування оцінок впливу для m факторів , що залишилися.

Розберемо на прикладі моделі (2) як знаходяться стандартні помилки оцінок параметрів a і b. Для цього знайдемо діагональні елементи матриці , С₁₁ і С₂₂.

З (23) і (24) випливає, що

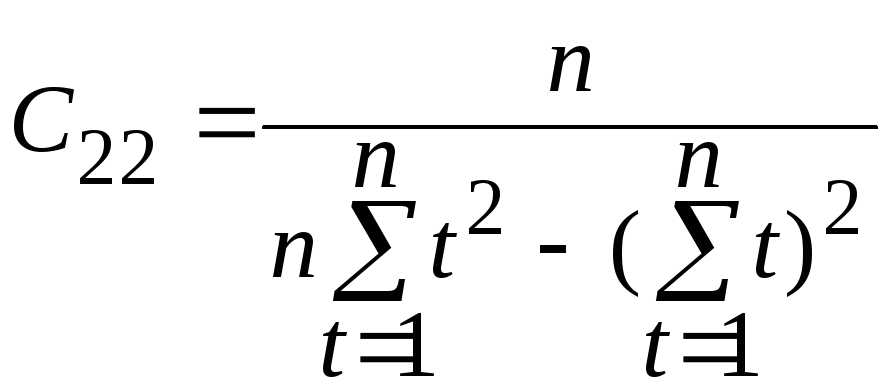
Тоді

де , m = 1.

Зауваження 2. Звичайно в парної регресії перевіряється значимість тільки коефіцієнта b [4].

в) Для оцінки якості отриманої моделі залежності вводиться коефіцієнт детермінації. Очевидно, чим ближче спостереження Y(t) примикають до отриманої лінії регресії (моделі залежності) , тим краще модель описує відповідну істину залежність (тренд) часового ряду і з більшою надійністю вона може бути застосована для практичних розрахунків. Тому коефіцієнт детермінації вводиться як

(26)

де

m - число факторів у моделі.

З визначення випливає, що коефіцієнт детермінації характеризує частку, що пояснюється моделлю , дисперсії в загальній величині дисперсії перемінної .

Статистична значимість коефіцієнтів детермінації перевіряється за допомогою F-критерію в такий спосіб [4], обчислюється величину

(27)

Якщо (m; v), де - табличне значення F-критерію для рівня значимості і числа ступенів свободи m і v = n-(m+1), то коефіцієнт детермінації вважається значущим. Тому, що з (26) і (27) випливає, що

, (28)

то значимість коефіцієнта детермінації означає адекватність отриманої моделі істинної залежності (тренду) часового ряду.

Зауваження 3. У випадку парних регресій (2) - (5) можна показати, що , де r = r_yx - коефіцієнт кореляції, а _- індекс кореляції або кореляційне відношення між Y(t) і X(t). [4] Тому, що для парної лінійної залежності , то у випадку значимості значиме й r, отже , і навпаки. Тому досить перевірити на адекватність отриману модель без перевірки значимості коефіцієнтів моделі або навпаки.

г) Розглянемо питання про автокореляцію залишків. При застосуванні методу найменших квадратів ми виходимо з гіпотези, що помилки E(t) представляють при різних t випадкові незалежні (некорелюючі) величини . Однак при роботі з часовими рядами таке допущення далеко не завжди вірне. Якщо вигляд моделі обраний невдало, то навряд чи можна говорити про те, що відхилення є незалежними. У цьому випадку звичайно спостерігається помітна концентрація позитивних і негативних відхилень від регресії і можна сумніватися в їхньому випадковому характері. Якщо послідовні значення E(t) корелюють між собою, то говорять, що має місце автокореляція помилок. Метод найменших квадратів і у випадку автокореляції дає незміщені й достатні оцінки. [3] Однак отримана за наявності високої автокореляції стандартна помилка має мало змісту в силу своєї ненадійності. А це призводить до неефективних оцінок параметрів із різким збільшенням їхніх стандартних помилок . У всякому разі, значна автокореляція говорить про те, що є невраховані фактори, що істотно впливають на , або вигляд моделі підібраний не зовсім вдало. Тому при аналізі відповідної моделі необхідно визначити, чи є у наявності автокореляція в , чи немає. Одним із самих простих і досить обгрунтованих прийомів виявлення автокореляції є метод Дарбіна - Уотсона. У основі методу лежить критерій, пов'язаний із гіпотезою про існування автокореляції першого порядку, тобто автокореляції між сусідніми членами часового ряду з =E(t). Відповідний критерій має вигляд:

(29)

Припускаючи, що , тому, що при великому n ці дві суми мало відрізняються одна від одної, одержимо

(30)

Якщо автокореляція відсутня, то і . Якщо існує повна автокореляція, то і, у випадку позитивної автокореляції, , а у випадку негативної автокореляції .

Для d-статистики знайдені критичні межі ( - верхня і - нижня), що дозволяють прийняти або відхилити гіпотезу про відсутність автокореляції при - ому рівні значимості й виборці обсягу n. Якщо

1) , то автокореляція відсутня;

2) або , то нічого про наявність або відсутність автокореляції не можна сказати;

3) , то існує позитивна автокореляція, , то існує негативна автокореляція з довірчою імовірністю .

Таким чином, якщо за критерієм Дарбіна - Уотсона виявлена істотна автокореляція залишків отриманого рівняння регресії (моделі ), то це означає необхідність або зміни моделі з додаванням нових факторів, або взагалі зміни вигляду моделі, тобто добору іншої залежності.

Більш зручним критерієм для перевірки автокореляції, на наш погляд, є критерій Неймана. Як статистика, використовується середня Неймана.

(31), де

Якщо обчислене за (31) Q менше деякого табличного QL, то для рівня значимості існує позитивна автокореляція залишків, якщо Q більше деякого табличного QU, то існує негативна автокореляція залишків. Для

;

;

.

Можна показати [2], що якщо , то . (32)