Преобразуем теперь условия другой системы.

1. .

2. .

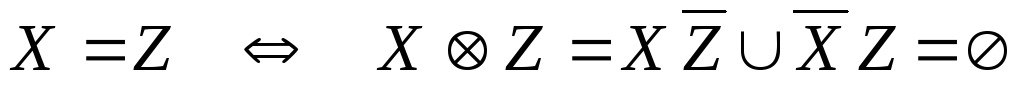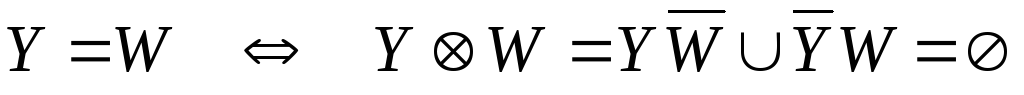Объединяя полученные условия в одно, имеем:

. На рис. 5 отмечаем пустые клетки этого условия.

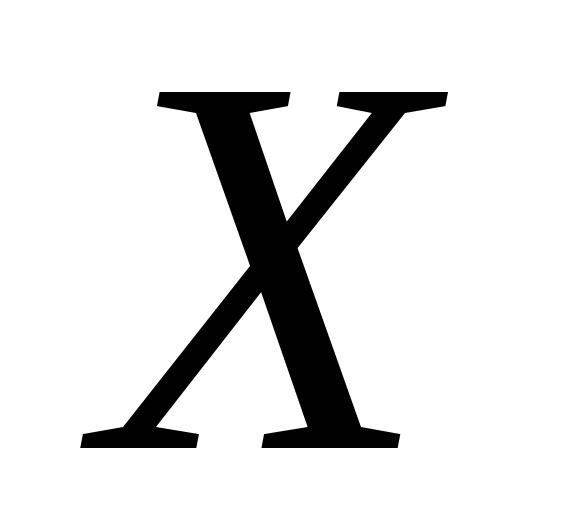
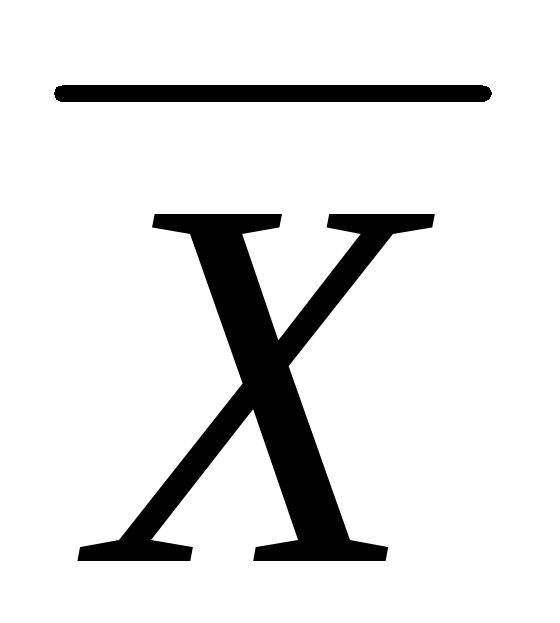
		Ø	Ø
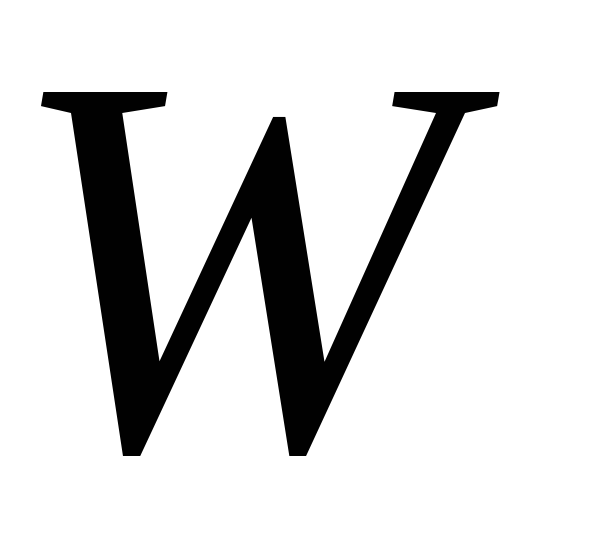
	Ø	Ø	Ø	Ø
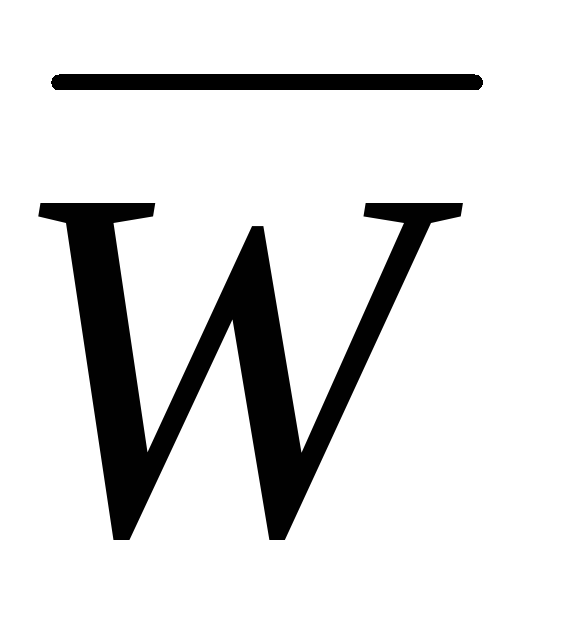
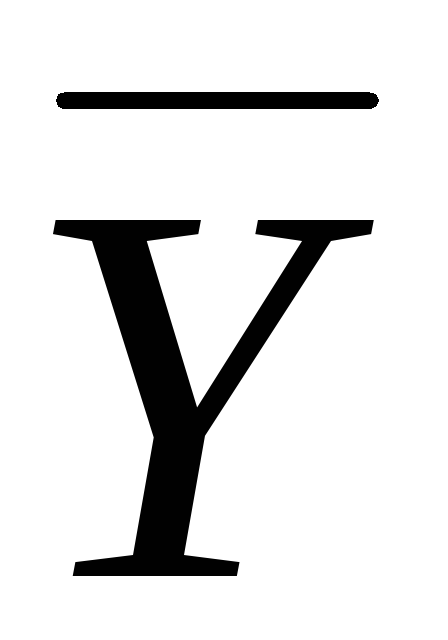
	Ø	Ø	Ø	Ø
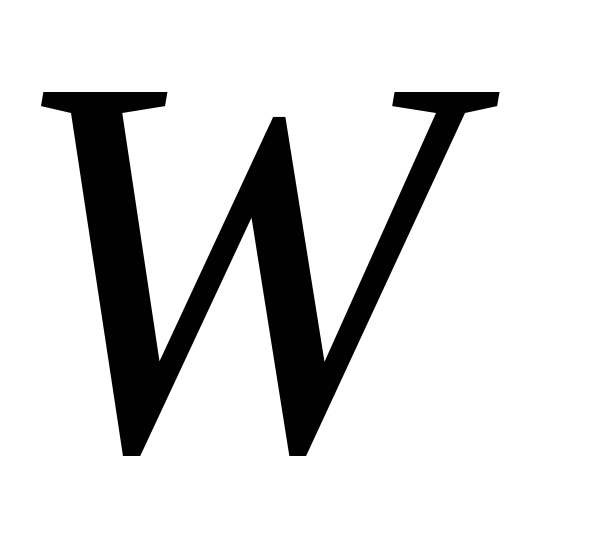
		Ø	Ø

Рис. 5

Сравнивая диаграммы, изображенные на рис.4 и рис.5, замечаем, что все пустые клетки диаграммы (рис.5) также пусты и на диаграмме (рис.4). Следовательно, утверждение верно.

С другой стороны, замечаем, что на рис.4 клетка равна Ø, а на рис.5 – нет, тогда заключаем, что соответствующие условия не равносильны. Действительно, если , то , что противоречит рис.4.

Пример 2. Доказать тождество:

.

Решение. Для доказательства этого тождества воспользуемся диаграммой Венна.

Рис. 6 Рис. 7

На рис. 6 двойная штриховка задаёт левую часть тождества, причём горизонтальная штриховка задаёт множество , а вертикальная – множество .

На рис. 7 горизонтальная штриховка задаёт множество , вертикальная – множество , тогда заштрихованные каким-либо образом клетки диаграммы задают правую часть тождества.

Таким образом, диаграммы Венна для левой и правой частей тождества совпадают, значит левая и правая части тождества задают одно и тоже множество. Тождество доказано.

§ 4. Уравнения и системы уравнений в алгебре множеств

В алгебре множеств имеется своя теория уравнений, значительно отличающаяся от той, которую мы знаем из курса алгебры. Рассмотрим метод решения одного уравнения с одним неизвестным.

Пусть – подмножества некоторого универсального множества , связанные формулами , где X — неизвестное множество. Множество называется решением уравнения

, (1)

если формулы задают одно и то же множество.

Совокупность всех частных решений есть общее решение уравнения (1).

По лемме 2 уравнение (1) равносильно уравнению:

. (2)

При помощи основных тождеств 1-18 алгебры множеств уравнение (2) приводится к виду:

, (3)

где A , B и C — некоторые множества.

Уравнение (3) равносильно системе условий:

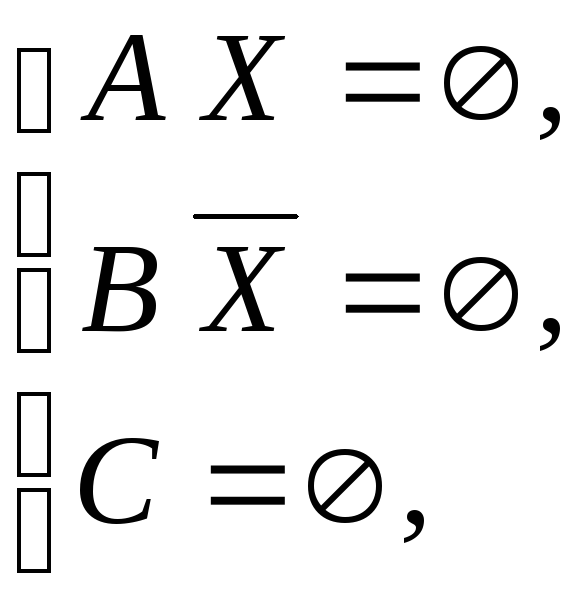
которые в свою очередь можно записать в виде:

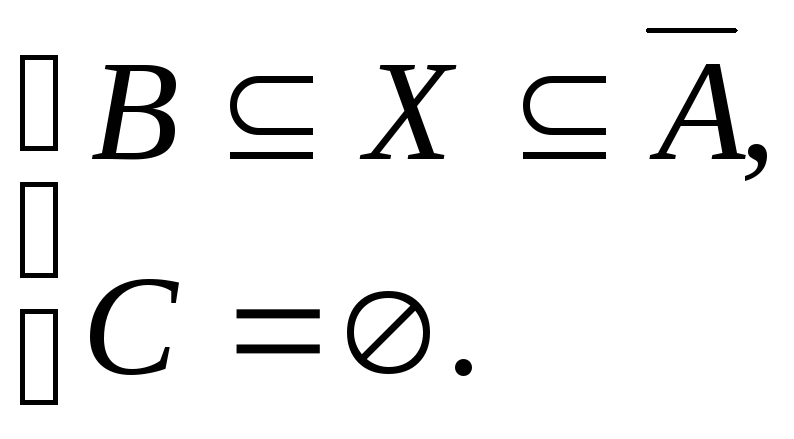(4)

Уравнение (1) имеет решение тогда и только тогда, если A , B и C удовлетворяют следующей системе условий:

, (5)

которая равносильна одному условию:

. (6)

Условия (5) или (6) представляют собой необходимые и достаточные условия существования решения уравнения (1).

Решением является любое множество, удовлетворяющее условию: Нетрудно заметить, что различные решения уравнения получаются при добавлении к “наименьшему” (по числу элементов) решению любых подмножеств разности . Всего таких подмножеств будет – это число различных решений уравнения (1).

Можно записать общее решение “в параметрической форме”: или , где параметр K – произвольное множество из U.

Пример 1. Решить уравнение: .

Найти необходимые и достаточные условия, при которых уравнение имеет решение. Оценить число решений уравнения.

Решение. Данное уравнение равносильно следующему: .

Преобразуем его к уравнению вида (3):

, откуда получаем:

Отсюда необходимые и достаточные условия существования решения следующие:

Первое условие выполнено при любых A и B. Тогда, решение уравнения существует при условии ; решением является любое множество X, удовлетворяющее условию .

Запишем решение в параметрической форме:

, где K – произвольное множество из U. Нетрудно заметить, что так как , то . Таким образом, заключаем, что число различных решений уравнения равно числу подмножеств множества , которое равно .

Проиллюстрируем теперь решение этого примера на диаграмме Венна, причём коэффициенты уравнения будем отмечать по вертикали, а неизвестное X – по горизонтали. Приводим исходное уравнение к виду (3): .

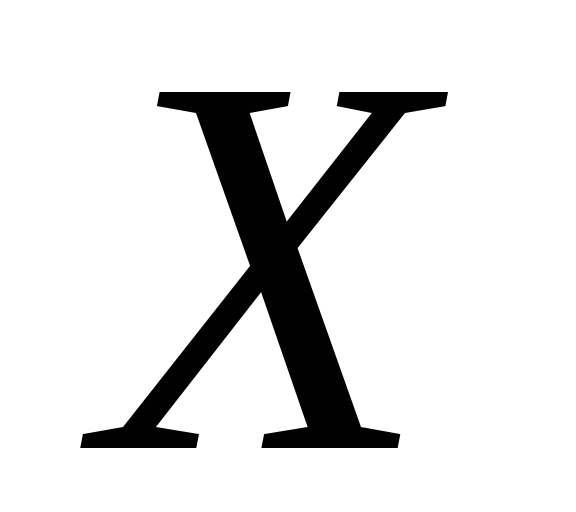
	(1) Ø		(1,3) Ø
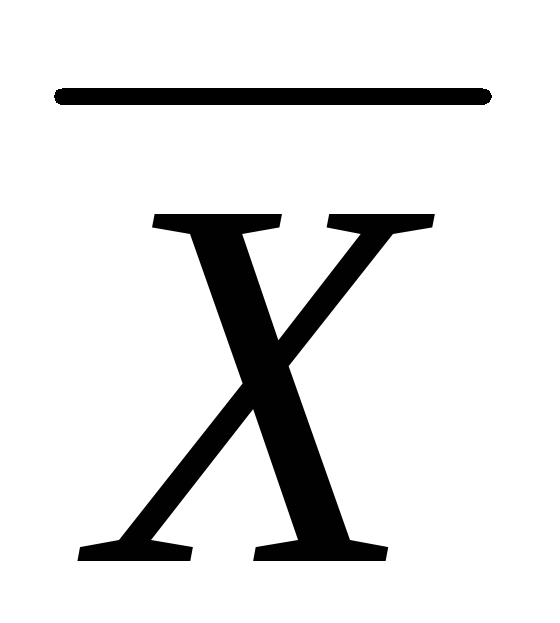
		(2) Ø	(3) Ø

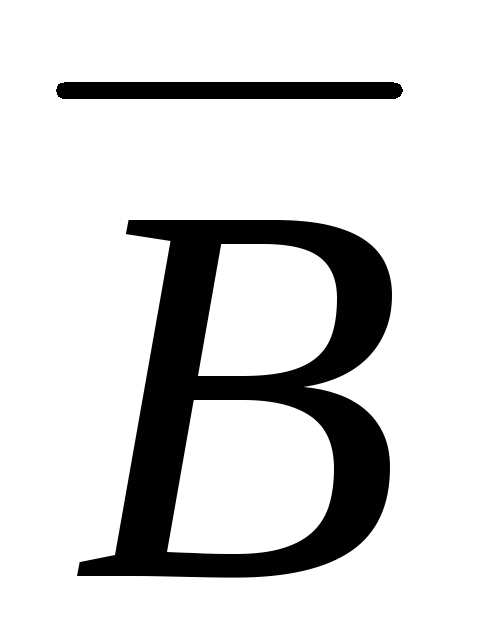
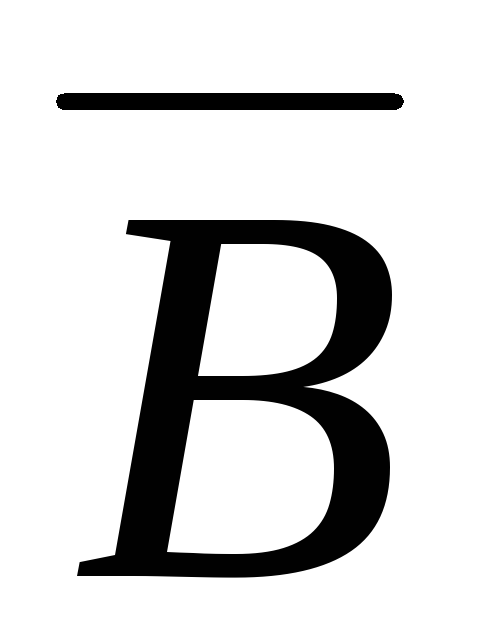
Рис. 8

Условие на диаграмме (рис.8) отмечено цифрой 1, условие — цифрой 2, а условие — цифрой 3.

Необходимое и достаточное условие существования решения задаётся множеством тех клеток диаграммы, которые пусты по вертикали и тем самым определяют условие, которое не зависит от X. В нашем примере это условие задаётся двумя клетками, которые соответствуют множеству , т.е..

Решение X образует множество элементов универса, расположенных в двух заштрихованных клетках диаграммы, причём “наименьшим” решением является множество (т.к. ), а “наибольшим” — множество .

Получаем, что решением является любое множество X, удовлетворяющее условиям .

Найдём теперь по диаграмме Венна общее решение в параметрической форме. Объединяя “наименьшее” решение с произвольным подмножеством множества , получаем (т.к. ). Число различных решений уравнения определяется числом подмножеств множества , которое равно .

Рассмотрим решение исходного уравнения для конкретных множеств . Пусть . Тогда , , решение X принадлежит множеству. Получили четыре решения.

Проверка. Подставив в уравнение, получаем.

Ответ: уравнение имеет решение при условии, что .

Системы уравнений с одним неизвестным .

Рассмотрим систему n уравнений с неизвестным X:

,

где .

Каждое из уравнений с помощью тождественных преобразований приведём к равносильному уравнению вида (3):

Объединяя все уравнения в одно, получим:

Таким образом, заданная система уравнений сводится к уравнению вида (3), решение которого мы уже знаем.

Пример 2. Решить систему уравнений:

.

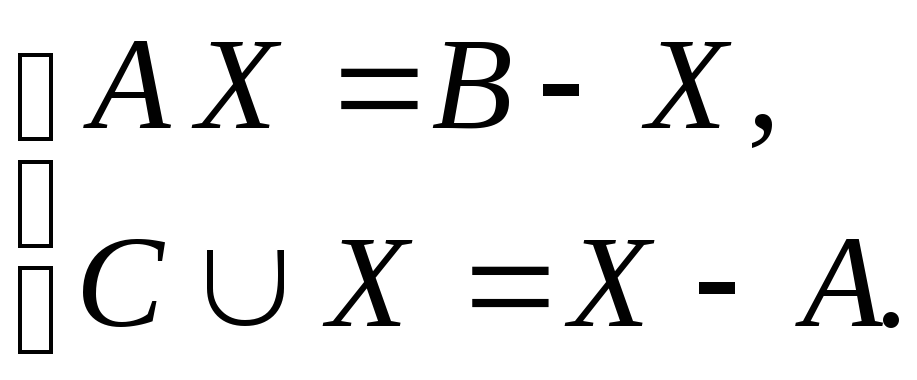Найти необходимые и достаточные условия, при которых система имеет решение. Оценить число решений системы уравнений.

Решение. При помощи равносильных преобразований приведём исходную систему уравнений к уравнению вида (3).

Таким образом, приходим к уравнению:

.

Решая это уравнение, получаем, что решением является любое множество X, удовлетворяющее условиям , причём решение существует при условии: .

Отсюда получаем необходимое и достаточное условие существования решения системы: .

Запишем теперь решение системы в параметрическом виде: , где параметр K — любое множество универса. Отсюда заключаем, что число решений системы равно числу подмножеств множества , которое равно .

Построим для этого примера диаграмму Венна, цифрой 1 (рис.9) отметим условие , цифрой 2 — условие , а цифрой 3 — условие .

(1,3) Ø	(1) Ø	(1,3) Ø	(1) Ø
(2,3) Ø	(2) Ø	(2,3) Ø		(2) Ø	(2) Ø	(2) Ø

Рис. 9

Три первых пустых столбца диаграммы дают необходимое и достаточное условие существования решения системы. Это условие можно записать в виде

.

Решение X расположено в четырёх заштрихованных клетках диаграммы. “Наименьшее” решение (по числу элементов) можно записать в виде:

, т. к. , а “наибольшее” – в виде: .

Тогда решением X является любое множество, удовлетворяющее условиям: , или в параметрическом виде: , где . Отсюда, число решений системы равно числу подмножеств множества , т.е. .

Проверка. Подставим в систему.

1) ,

.

2) ,

.

Получили, что каждое уравнение системы обращается в тождество.

Ответ: Необходимое и достаточное условие существования решения системы , решением является X – любое множество, удовлетворяющее условиям: , или в параметрическом виде: , где .