§ 3. Диаграммы Венна

Диаграммы Венна используются для наглядного представления о возможных отношениях между несколькими множествами.

Допустим дана система множеств в универсе Тип элемента относительно определяется тем, каким множествам из этот элемент принадлежит, а каким − нет. Элементы и однотипны, если они принадлежат одним и тем же множествам из или оба не принадлежат ни одному из них.

Легко понять, что диаграмма Венна для системы множеств представляет собой разбиение прямоугольника на клеток − по одной для каждого типа элементов.

При прямоугольник разбивается на 2 клетки:

Рис. 2

На рис. 3 показаны диаграммы Венна при и .

							*

Рис. 3

Из приведённых примеров легко понять, как можно построить диаграмму Венна для любого n: она получается из диаграммы для n-1 множеств после того, как мы разделим пополам все вертикальные (или горизонтальные) полосы и отнесём к все полосы с нечётными номерами, считая слева (сверху), а все полосы с чётными номерами отнесём к . Таким образом, каждая клетка предыдущей диаграммы разобьётся на две части, одна из которых относится к , а другая – к .

Тип элементов, лежащих в той или иной клетке, легко определить с помощью её указателей. Так, на рис.3 тип клетки, отмеченной *, есть , т.е. в ней располагаются элементы, принадлежащие множествам и , но не принадлежащие множеству .

Диаграмму Венна удобно использовать для доказательства тождеств, а также для упрощения условий.

Пример 1. Верно ли, что из условий:

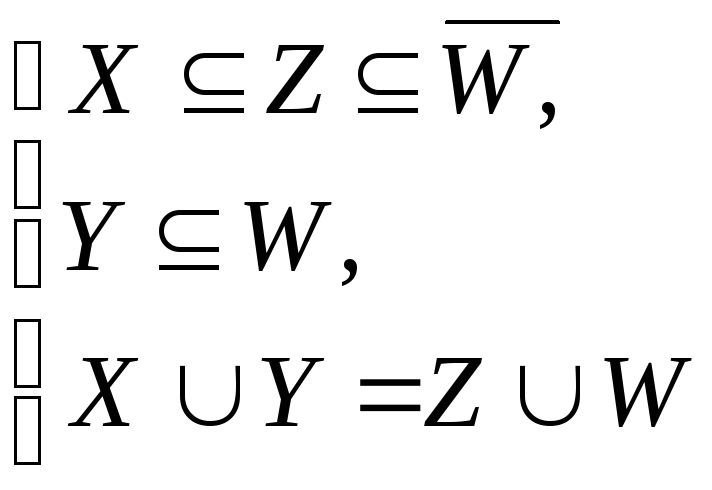следует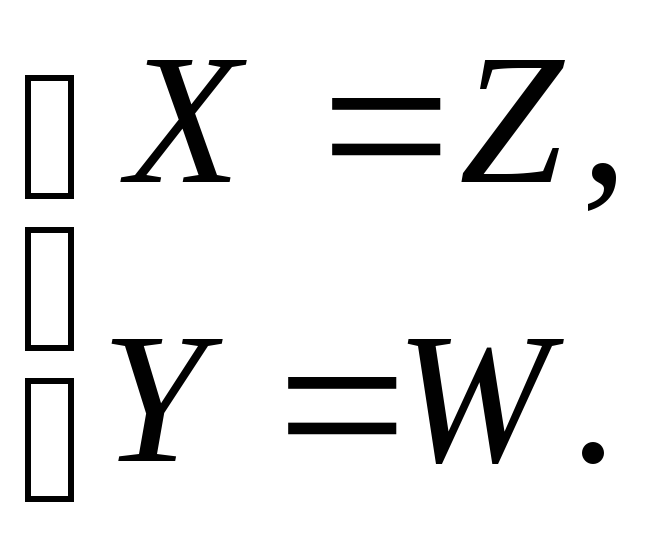

Решение. Данные условия равносильны следующим:

1. Ø.

2. Ø.

3. 

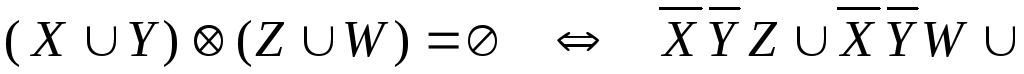
Объединив три условия в одно, получим:

.

После применения закона поглощения получаем:

Ø.

На диаграмме Венна (рис.4) отметим полученные условия.

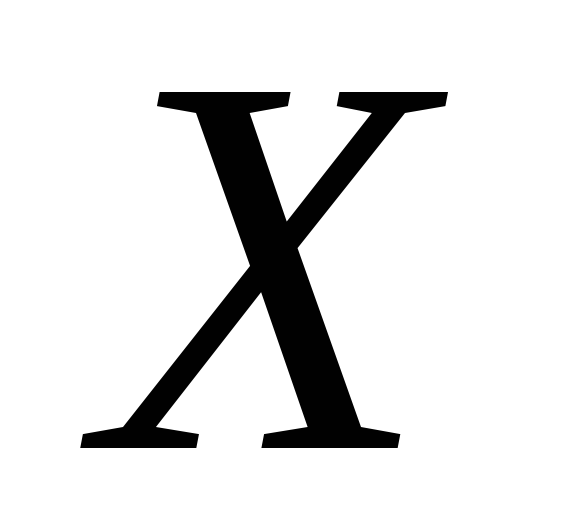
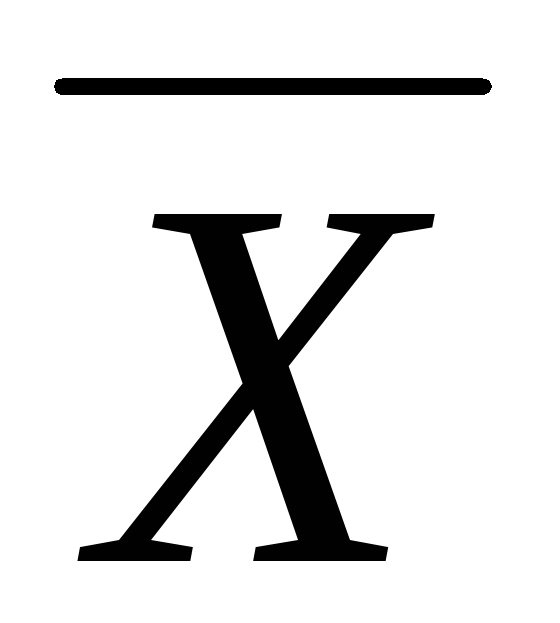
	Ø	Ø	Ø
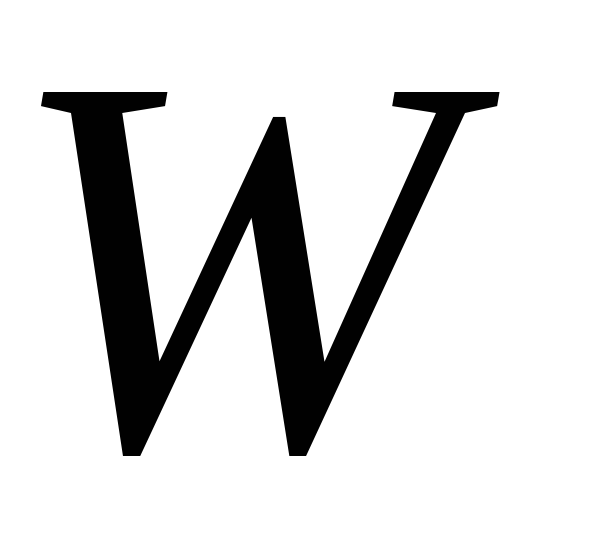
	Ø	Ø	Ø	Ø
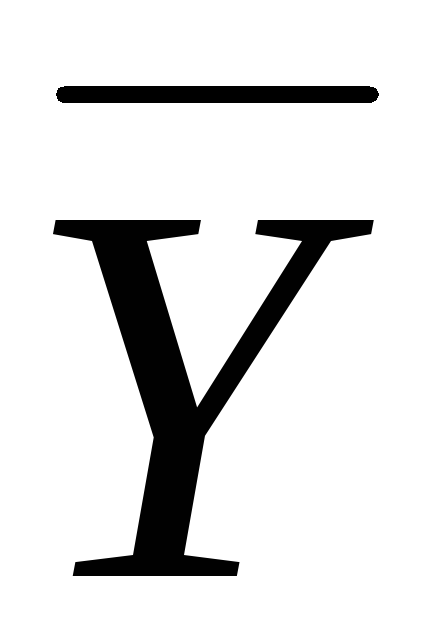
	Ø	Ø	Ø	Ø
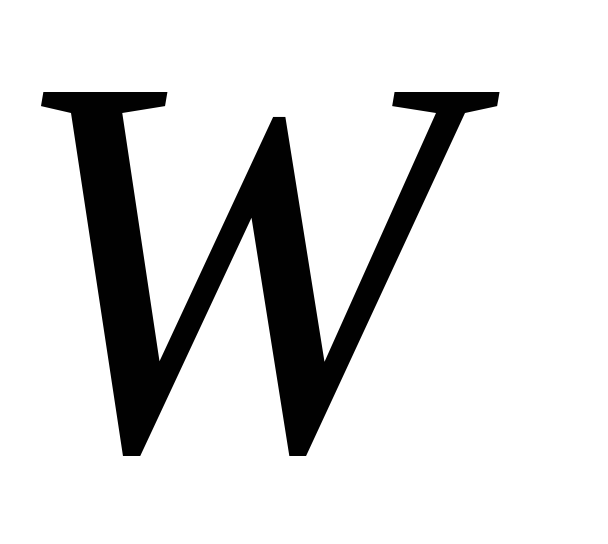
		Ø	Ø

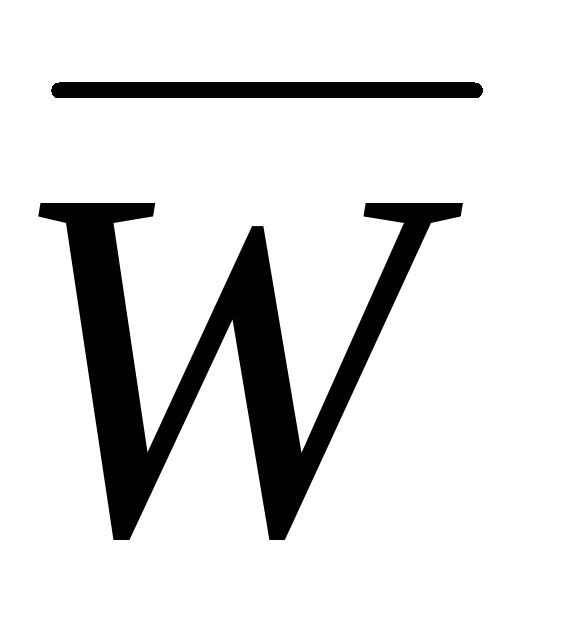
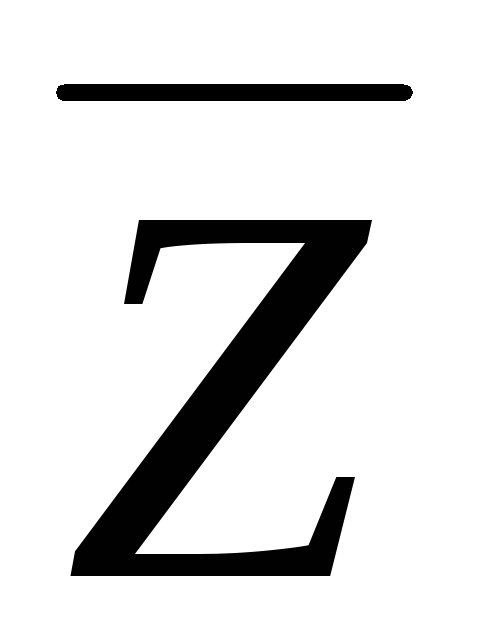
Рис. 4