Контрольная работа № 3

В задачах 161-180 найти неопределенные интегралы способом подстановки (методом замены переменной).

161.	171.
162.	172.
163.	173.
164.	174.
165.	175.
166.	176.
167.	177.
168.	178.
169.	179.
170.	180.

Решение типовых примеров.

1. Найти неопределенный интеграл .

Решение. Применим подстановку . Тогда и

.

2. Найти интеграл .

Решение. Применим подстановку . Тогда ; , откуда

.

В задачах 181‑200 найти неопределенные интегралы, используя выделение полного квадрата.

181. . 182. . 183. . 184. . 185.. 186. . 187.. 188. . 189.. 190. .

191.. 192. . 193. . 194. . 195.. 196. . 197. . 198. . 199.. 200. .

Решение типового примера. Найти интеграл .

Решение. Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом:

х² - 4х + 8 = х² – 4х + 4 = (х – 2)² + 2².

Тогда после подстановки получаем

При этом при вычислении интеграла мы воспользовались заменой переменной . Тогда , откуда

.

В задачах 201‑220 найти неопределенные интегралы, применяя метод интегрирования по частям.

201. . 202. . 203. . 204. . 205.. 206. . 207. . 208. . 209. . 210. .

211. . 212. . 213. . 214. . 215. . 216. . 217. . 218. . 219. . 220. .

Решение типовых примеров.

1. Найти интеграл .

Решение. Применим формулу интегрирования по частям

.

Положим, что . Тогда . Следовательно,

Найти интеграл .

Решение. Положим . Тогда . Отсюда

.

Применяя в последнем интеграле подстановку , получаем ,

следовательно,

Отсюда,

В задачах 221‑240 найти неопределенные интегралы, пользуясь разложением рациональных дробей на простейшие.

221.. 222. . 223. . 224. .	231.. 232.. 233. . 234. .
225. . 226. . 227. . 228. . 229. . 230. .	235. . 236. . 237. . 238. . 239. . 240. .

Решение типовых примеров.

1. Найти интеграл .

Решение. Разложим знаменатель на множители: .

Тогда

Освобождаемся от знаменателя:

.

Теперь приравниваем коэффициенты при одинаковых степенях х:

х² 0 = А + В; А = -В;

х¹ 1 = А – В + С;

х⁰ 0 = А – С; А = С.

Из второго уравнения получаем

1 = А + А + А = 3А; А = .

Отсюда А = ; В = -; С = .

Следовательно,

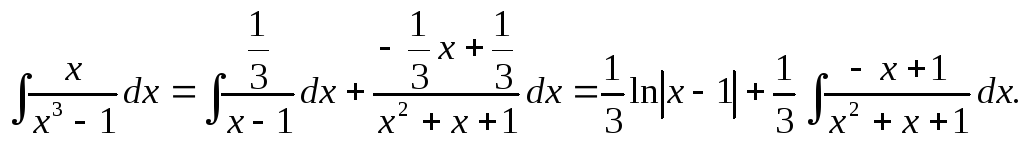
Воспользуемся равенством

х² + х + 1 = х² + 2*

После замены переменной t = x + , dt = dx, x = t - и

Ответ:

2. Найти интеграл

Решение. Из равенства

получаем .

Приравниваем коэффициенты при одинаковых степенях :

х² 0 = А + В; А = -В;

х¹ 1 = А – В + С;

х⁰ 0 = А – С; А = С.

Отсюда А = ; В = -; С = . Таким образом,

В задачах 241‑260 вычислить площадь фигуры, ограниченной заданными параболами.

241. у=х2 + х + 2 у= -х2 – 5х + 7	251. у=х2 + 3х - 2 у= -х2 – х + 3
242. у = -х2 + 4х – 1 у = х + 2х + 9	252. у = 3х2 + 5х – 2 у = -3 х – 4х – 3
243. у= 2х2+ 6х - 3 у= - х + х + 5	253. у= х2 – 3х – 4 у= - х – х + 8
244. у = х2 + 2х – 2 у = -х2 - 2х – 3	254. у =-х2 + 2х – 5 у = х2 – 2х+ 7
245. у= х2 – 3х – 1 у= -х2 – 2х + 5	255. у= 2х2 + 4х – 7 у= -х2 – х +1
246. у = х2 + 3х – 5 у = -х2 + 3х + 2	256. у = -х2 + 2х – 1 у = 2х2 + 2х + 5
247. у=х2 – 2х + 4 у= -х2 – х + 2	257. у = х2 + 2х – 5 у = -х2 - 3х + 3
248. у= 2х2 – 6х – 2 у= -х2 + х – 4	258. у = 2х2 + 8х – 5 у = -2х2 + 6х – 3
249. у = х2 + 5х – 3 у = -х2 – 7х + 4	259. у=х2 - 3х– 2 у= -х2 – 7х + 3
250. у = х2 +5х – 2 у = -х2 – 3х + 2	260. у= х2 – 2х – 5 у= -х2 – х + 1

Решение типового примера. Вычислить площадь, ограниченную параболами (рис. 4) )

у = 2х² – х – 2;

у = -х² + х – 1.

Решение. Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:

2х² – х – 2 = -х² + х – 1.

Отсюда 3х² – 2х – 1 = 0, D = 16,

х₁ = , х₂ = .
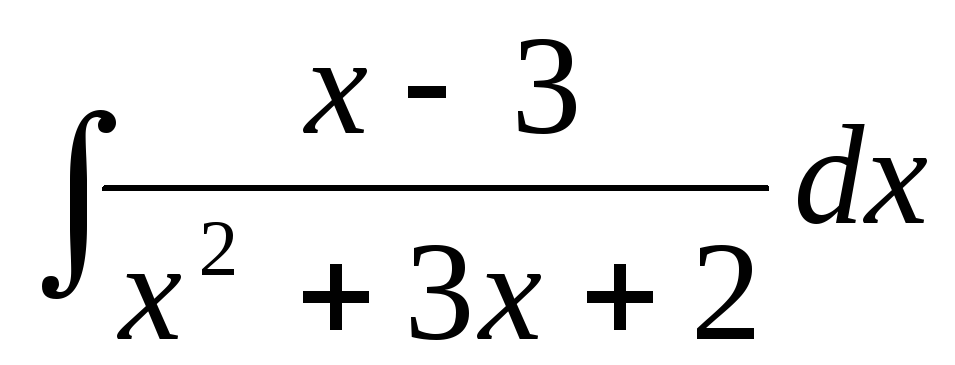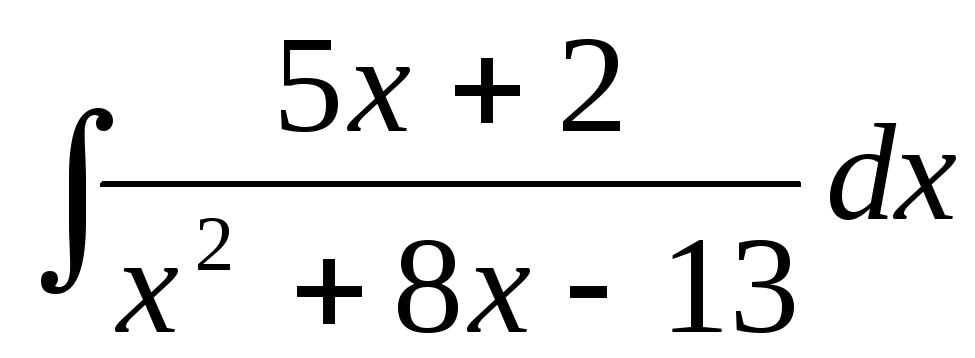