Вопросы для самопроверки

1. Как определяется сумма и разность двух векторов?

2. Дайте определение коллинеарных и компланарных векторов.

3. Дайте определение проекции вектора на ось.

4. Как выглядит разложение вектора в системе орт на плоскости и в пространстве? Что такое координаты вектора?

5. Каковы свойства скалярного произведения векторов?

6. Как найти угол между векторами? Как найти длину вектора по его координатам?

7. Каково условие перпендикулярности двух векторов?

8. Как найти вектор, перпендикулярный двум данным векторам?

9. Как найти площадь треугольника, построенного на двух векторах?

10. Как найти объём пирамиды с вершинами в заданных точках?

11. Как выглядит условие компланарности трёх векторов?

12. Что Вы можете сказать о соответственных координатах двух коллинеарных векторов?

13. Как выглядит уравнение плоскости, проходящей: а) через заданную точку с заданным нормальным вектором; б) через три заданные точки?

14. Напишите формулу для вычисления угла между двумя плоскостями.

15. Какие Вы знаете виды уравнений прямой в пространстве?

16. Как выглядит формула для отыскания угла между двумя прямыми в пространстве.

17. Как найти координаты точки пересечения плоскости и прямой?

18. Как найти расстояние от заданной точки до заданной плоскости?

Контрольная работа №1

В задачах 1-20 решить заданную систему уравнений, пользуясь формулами Крамера. Сделать проверку полученного решения.

1.	11.
2.	12.
3.	13.
4.	14.
5.	15.
6.	16.
7.	17.
8.	18.
9.	19.
10.	20.

Решение типового примера. Пусть требуется, используя формулы Крамера, решить систему

Подсчитаем сначала главный определитель системы , воспользовавшись следующим правилом вычисления определителей третьего порядка:

.

У нас

.

Так как ≠0, делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители , , .

,

,

.

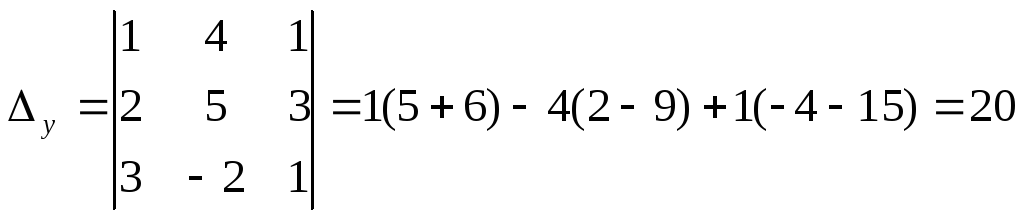Далее, воспользовавшись формулами Крамера, окончательно получим

Осуществим проверку правильности полученного решения, подставив его в каждое уравнение заданной системы:

0-2·(-1)+2=4,

2·0+(-1)+3·2=5,

3·0+4·(-1)+2=-2.

Все три равенства верные, поэтом делаем вывод о правильности полученного ранее решения x=0, y=-1, z=2.

В задачах 21-40 даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ, 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол В в радианах с точностью до 0,01; 4) уравнение медианы АЕ; 5) уравнение и длину высоты СD; 6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и точку М её пересечения с высотой СD.

21. А(-8; -3), В(4; -12), С(8; 10).

22. А(-5; 7), В(7; -2), С(11; 20).

23. А(-12; -1), В(0; -10), С(4; 12).

24. А(-10; 3), В(2; 0), С(6; 22).

25. А(0; 0), В(3; 4), С(4; 2).

26. А(0; 2), В(12; -7), С(16; 15).

27. А(-9; 6), В(3; -3), С(7; 19).

28. А(3; -3), В(6; 1), С(7; -1).

29. А(1; 0), В(13; -9), С(17; 13).

30. А(4; 0), В(7; 4), С(8; 2).

31. А(-2; 7), В(10; -2), С(8; 12).

32. А(-6; 8), В(6; -1), С(4; 13).

33. А(0; 2), В(3; 6), С(4; 4).

34. А(-10; 5), В(2; -4), С(0; 10).

35. А(-4; 12), В(8; 3), С(6; 17).

36. А(-3; 10), В(9; 1), С(7; 15).

37. А(4; -3), В(7; 1), С(8; -1).

38. А(2; -2), В(5; 2), С(6; 0).

39. А(-1; 1), В(2; 5), С(3; 3).

40. А(-5; 9), В(7; 0), С(5; 14).

Решение типового примера. Пусть А(-1;2), В(5;-1), С(-4;-5).

1. Расстояние d между точками A(x₁ ; y₁) и B(x₂; y₂) определяется по формуле

d= (1)

воспользовавшись которой находим длину стороны АВ :

2. Уравнение прямой, проходящей через две заданные точки плоскости А(x₁;y₁) и B(x₂;y₂) имеет вид

(2)

Подставляя в (2) координаты точек А и В, получаем уравнение стороны АВ:

Угловой коэффициент прямой АВ найдём, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом .

У нас то есть откуда

Аналогично получим уравнение прямой ВС и найдём её угловой коэффициент :

Далее т.е.

3. Для нахождения внутреннего угла нашего треугольника воспользуемся формулой

(3)

Отметим, что порядок вычисления разности угловых коэффициентов, стоящие в числителе этой дроби, зависит от взаимного расположения прямых АВ и ВС. Подумайте, как бы Вы стали искать внутренние углы А и С треугольника АВС?

Подставив ранее вычисленные значения и в (3), находим:

Теперь, воспользовавшись таблицами В.М. Брадиса или инженерным микрокалькулятором, получаем рад.

4. Для составления уравнения медианы АЕ найдём сначала координаты точки Е, которая лежит на середине отрезка ВС:

Теперь, подставив в (2) координаты точек А и Е, получаем уравнение медианы:

5. Для составления уравнения высоты CD воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом , которое имеет вид

(4)

и условием перпендикулярности прямых АВ и СD, которое выражается соотношением , откуда Подставив в (4) вместо значение , а вместо координаты точки С, получим уравнение высоты CD:

(CD).

Для вычисления длины высоты CD воспользуемся формулой отыскания расстояния d от заданной точки до заданной прямой с уравнением , которая имеет вид

(5)

Подставив в (5) вместо координаты точки С, а вместо А, В, С коэффициенты уравнения прямой АВ, получаем

6. Так как искомая прямая EF параллельна прямой АВ, то . Подставив в уравнение (4) вместо x_0, y₀ координаты точки Е, а вместо значение , получаем уравнение прямой EF:

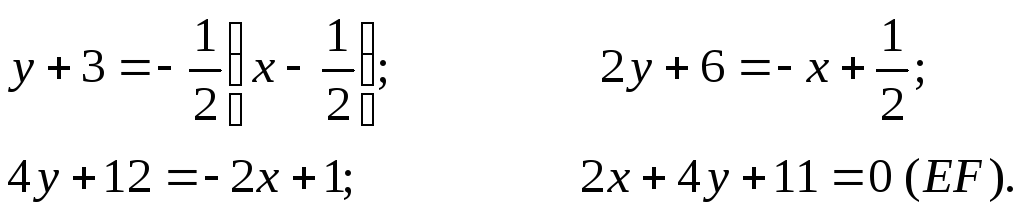
Для отыскания координат точки М решаем совместно уравнения прямых EF и CD:

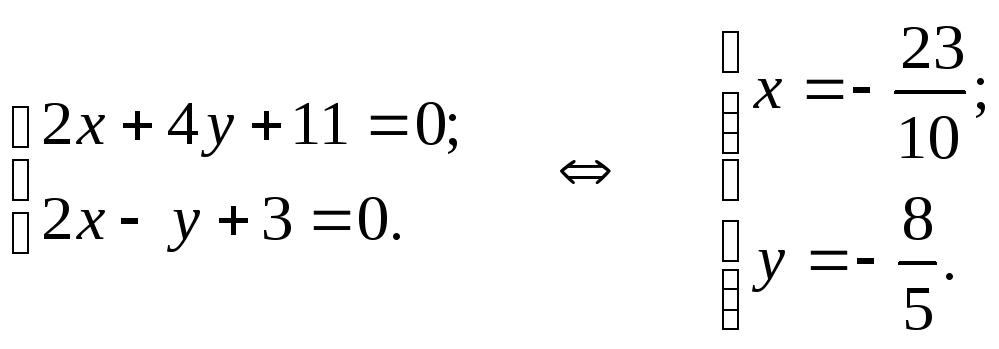
Таким образом, .

Треугольник АВС, высота CD, медиана AE, прямая EF и точка М построены в системе координат xOy на рис. 1.

В задачах 41-60 даны координаты вершин пирамиды ABCD. Требуется:

1. Записать векторы в системе орт и найти модули этих векторов;

2. Найти угол между векторами ;

3. Найти проекцию вектора на вектор ;

4. Найти площадь грани АВС;

5. Найти объём пирамиды ABCD;

6. Составить уравнение ребра АС;

7. Составить уравнение грани АВС.

41. А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2).

42. А(5; -1; -4), В(9; 3; -6), С(7; 10; -4), D(5; 1; -3).

43. А(1; -4; 0), В(5; 0; -2), С(3; 7; -10), D(1; -2; 1).

44. А(-3; -6; 2), В(1; -2; 0), С(-1; 5; -8), D(-3; -4; 3).

45. А(-1; 1; -5), В(3; 5; -7), С(1; 12; -15), D(-1; 3; -4).

46. А(-4; 2; -1), В(0; 6; -3), С(-2; 13; -11), D(-4; 4; 0).

47. А(0; 4; 3), В(4; 8; 1), С(2; 15; -7), D(0; 6; 4).

48. А(-2; 0; -2), В(2; 4; -4), С(0; 11; -12), D(-2; 2; -1).

49. А(3; 3; -3), В(7; 7; -5), С(5; 14; -13), D(3; 5; -2).

50. А(4; -2; 5), В(8; 2; 3), С(6; 9; -5), D(4; 0; 6).

51. А(-5; 0; 1), В(-4; -2; 3), С(6; 2; 11), D(3; 4; -9).

52. А(1; -4; 0), В(2; -6; 2), С(12; -2; 10), D(9; 0; 8).

53. А(-1; -2; -8), В(0; -4; -6), С(10; 0; 2), D(7; 2; 0).

54. А(0; 2; -10), В(1; 0; -8), С(11; 4; 0), D(8; 6; -2).

55. А(3; 1; -2), В(4; -1; 0), С(14; 3; 8), D(11; 5; 6).

56. А(-8; 3; -1), В(-7; 1; 1), С(3; 5; 9), D(0; 7; 7).

57. А(2; -1; -4), В(3; -3; -2), С(13; 1; 6), D(10; 3; 4).

58. А(-4; 5; -5), В(-3; 3; -3), С(7; 7; 5), D(4; 9; 3).

59. А(-2; -3; 2), В(-1; -5; 4), С(9; -1; 12), D(6; 1; 10).

60. А(-3; 4; -3), В(-2; 2; -1), С(8; 6; 7), D(5; 8; 5)..

Решение типового примера. Пусть А(0; 0; 1), В( 2; 3; 5), С(6; 2; 3), D(3; 7; 2).

1. Известно, что произвольный вектор представляется в системе орт по формуле

(1)

где ­ координаты вектора в системе координат, порождённой ортами, причём

Если заданы точки , то для вектора

то есть

(2)

Воспользовавшись формулой (2) и координатами заданных точек A, B, C, D, получим:

Если вектор задан формулой (1),то его модуль вычисляется следующим образом:

(3)

Используя формулу (3), получаем модули найденных векторов:

Известна формула

где ­ скалярное произведение векторов и , которое можно вычислить следующим образом:

У нас

то есть .

3. Известно, что

,

то есть в нашем случае

4. Воспользуемся формулой нахождения площади треугольника, построенного на векторах и

где ­ векторное произведение векторов, которое можно вычислить по следующему правилу:

.

В нашем примере , причём

Таким образом,

(кв. ед.).

Объём пирамиды, построенной на трёх некомпланарных векторах можно найти по формуле

где ­ смешанное произведение векторов, которое вычисляется следующим образом:

.

У нас , где

,

то есть (куб.ед.).

6. Известно, что уравнение прямой, проходящей через две заданные точки пространства , имеет вид:

(4)

Подставив в (4) координаты точек А и С, получим

то есть уравнение ребра АС окончательно запишется следующим образом:

или .

7. Уравнение плоскости, проходящее через три заданные точки можно записать в виде

Подставляя в него координаты точек А, В, С, получим