8. Задача коммивояжера

Коммивояжеру, находящемуся в Париже, необходимо посетить три города. Он получил информацию о стоимости проезда самолетом в каждый из выбранных городов и стоимость проезда из одного города в другой. На основе добытых данных он составил матрицу стоимостей (см. табл.) проезда в выбранные города и обратно. Зная матрицу стоимостей коммивояжеру надо так составить маршрут путешествия, чтобы затраты на путешествие были бы минимальными и чтобы выполнялось требование: каждый пункт посещается только один раз.

Пункты	Париж	Берлин	Рим	Лондон
Париж	0	270	430	160
Берлин	70	0	160	10
Рим	200	130	0	350
Лондон	210	160	250	0

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

0x₁₁+270 x₁₂+430 x₁₃+160 x₁₄+70 x₂₁+0 x₂₂+160x₂₃+10x₂₄+200 x₃₁+130x₃₂+0 x₃₃+ +350 x₃₄+210 x₄₁+160x₄₂+250 x₄₃+0 x_44 min,

Ограничения имеют вид:

x₁₁+x₂₁+x₃₁+x₄₁=1,

x₁₂+x₂₂+x₃₂+x₄₂=1,

x₁₃+x₂₃+x₃₃+x₄₃=1.

x₁₄+x₂₄+x₃₄+x₄₄=1,

x₁₁+x₁₂+x₁₃+x₁₄=1,

x₂₁+x₂₂+x₂₃+x₂₄=1,

x₃₁+x₃₂+x₃₃+x₃₄=1,

x₄₁+x₄₂+x₄₃+x₄₄=1,

u₂-u₃+3 x_23 2,

u₂-u₄+3 x_24 2,

u₃-u₂+3 x_32 2,

u₃-u₄+3 x_34 2,

u₄-u₂+3 x_42 2,

u₄-u₃+3 x_43 2.

Вид электронной таблицы, созданной для решения задачи, представлен на рис. 40. Значения переменных x_ij располагаются в блоке B3:E6. В данном блоке ячейки, расположенные по диагонали обнулены (пункт назначения не может быть одновременно пунктом прибытия) и выделены, для удобства задания ограничений. Даны стоимости проезда из города в город (блок B11:E14). Для вычислений необходимо задать размерность задачи n (количество городов)- ячейка F16.

Рис. 40

Целевая функция расположена в ячейке F8. Ограничения находятся в блоках B7:E7 (коммивояжер въезжает один раз в каждый город) и F3:F6 (коммивояжер выезжает из каждого города один раз) (см. рис. 40 и 41). Вид электронной таблицы в режиме отображения формул представлен на рис. 41. В задаче коммивояжера есть ряд специфических ограничений по дополнительным переменным u_i (см. мат модель). Формулы этих ограничений находятся в блоке ячеек B17:E19. Значения самих переменных располагаются в блоке B8:E8.

На рис. 42 представлена запись условий задачи в окне "Поиск решения". Как известно, дополнительные переменные не относятся к целевой функции, но они, также как и x_ij, являются изменяемыми, поэтому адреса содержащих их ячеек должны быть введены в поле Изменяя ячейки одновременно с адресами переменных целевой функции.

Операцию ввода удобно проводить с помощью мыши. Необходимо установить курсор ввода в поле Изменяя ячейки, затем выделить мышью блок ячеек переменных целевой функции, нажать <Ctrl> и, удерживая эту клавишу, выделить мышью блок ячеек рабочего листа, отведенный для переменных u_i. В поле ввода адреса блоков отделяются ";" (см. рис. 42).

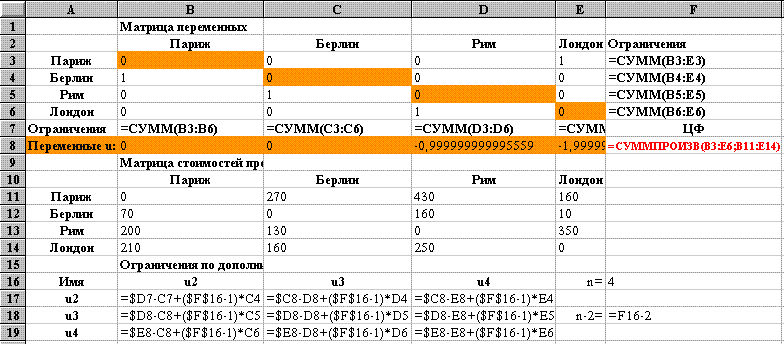
Рис. 41

Перечислим ограничения, которых не видно на рис. 42: $C$4=0; $D$5=0; $E$6=0; $F$3:$F$6=1.

Рис. 42

Первая запись в группе Ограничения представляет собой совокупность ограничений по дополнительным переменным u_i. Каждая ячейка блока в левой части неравенства содержит формулу одного ограничения (см. рис. 41 и мат. модель), правую часть представляет одно значение, равное n-2, содержащееся в F18. Такая запись означает, что каждая ячейка блока $B$17:$D$19 меньше либо равна 2 (4-2=2).

В поиске решения нельзя явно задать ограничение i j. Исходя из смысла переменных x_ij можно предположить, что значения тех x_ij, для которых i=j (расположенных по диагонали в блоке переменных), всегда должны быть равны 0 и ввести соответствующие ограничения. В группе Ограничения таких ограничений четыре: $B$3=0, $C$4=0, $D$5=0, $E$6=0.

По результатам поиска решения найден ответ задачи: из Парижа коммивояжер летит в Лондон, оттуда в Рим, затем в Берлин, откуда возвращается в Париж. Общая стоимость перелета составит 610 д. е. (см. рис. 40).