Практическое занятие № 16 Тема «Марковские процессы»

№1 Рассмотрим состояние банка, характеризующееся одной из процентных ставок: 2%, 3%, 4%, которые устанавливаются в начале каждого квартала и фиксированы на всем его протяжении. Таким образом, если за систему S принять рассматриваемый банк, то она в каждый момент времени может находится только в одном из следующих трех состояний: - процентная ставка 2%, - процентная ставка 3%, - процентная ставка 4%. Анализ работы банка в предшествующие годы показал, что изменение переходных вероятностей с течением времени пренебрежимо мало.

Определить вероятности указанных состояний банка в конце года, если в конце предыдущего года процентная ставка банка составляла 3%, а размеченный граф состояний банка представлен на рисунке.

S₁

S₂

S₃

0,4 0,3

0,2 0,3

0,2

0,1

№2 Предположим, что в условиях примера №1 переходные вероятности зависят от моментов установления процентных ставок. Матрицы переходных вероятностей задаются следующим образом:

. Построить размеченные графы состояний, соответствующие моментам времени - начало i-го квартала, i=1,2,3,4 и найти вероятности состояний банка в конце года, если в конце предшествующего года процентная ставка была 4%.

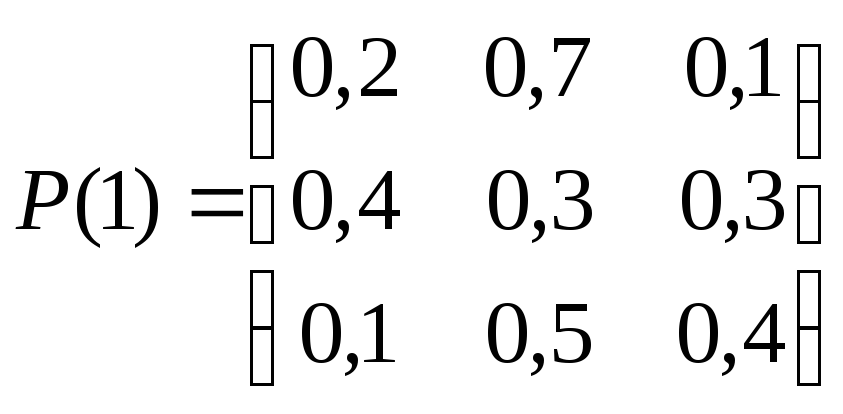
№3 Инвестиционный фонд размещает средства предприятий в наиболее ликвидные на рынке активы по одной из следующих годовых процентных ставок: 25%, 30%, 35%, которые устанавливаются фондом в начале каждого из рассматриваемых трех месяцев и остаются неизменными на всем его протяжении. Матрицы переходных вероятностей задаются следующим образом: . Построить размеченные графы состояний инвестиционного фонда, соответствующие рассматриваемым месяцам. Определить вероятности данных процентных ставок на третьем месяце, если в месяце, предшествующем первому из рассматриваемых месяцев, инвестиционный фонд мог разместить средства предприятий под 30% годовых.

№4 Рассмотрим состояние банка , , , характеризующееся соответственно процентными ставками 3%, 5%, 7%, 10%, которые устанавливаются в начале каждого месяца и фиксированы на всем его протяжении. Наблюдение за работой банка в предшествующий период показало, что переходные вероятности состояний в течение квартала остаются неизменными.

Определить вероятности состояний банка в конце квартала, если в конце предшествующего квартала процентная ставка составляла 55, а размеченный граф состояний банка имеет следующий вид:

S₁

0,6

0,2 0,1

S₂

S₃

0,3

0,4

S₄

0,3

0,3 0,4

№5 Допустим, что в условиях задачи №4 переходные вероятности зависят от моментов установления процентных ставок. Матрицы переходных вероятностей задаются следующим образом:

, , .

Постройте размеченные графы состояний, соответствующие началам каждого месяца в квартале, и найдите вероятности состояний банка в конце квартала, если в конце предшествующего квартала процентная ставка составляла 3%.