Практическое занятие №6 Тема «Целочисленные задачи линейного программирования. Метод Гомори»

Графическим методом и методом ветвей и границ решить задачу целочисленного программирования

№1

Ответ: =11 при х₁=1, х₂=5.

№2

,

Ответ: =29 при х₁=2, х₂=5.

Решить методом Гомори.

№3

Ответ:

№4

Ответ:

№5

Ответ:

№6

Ответ:

№7

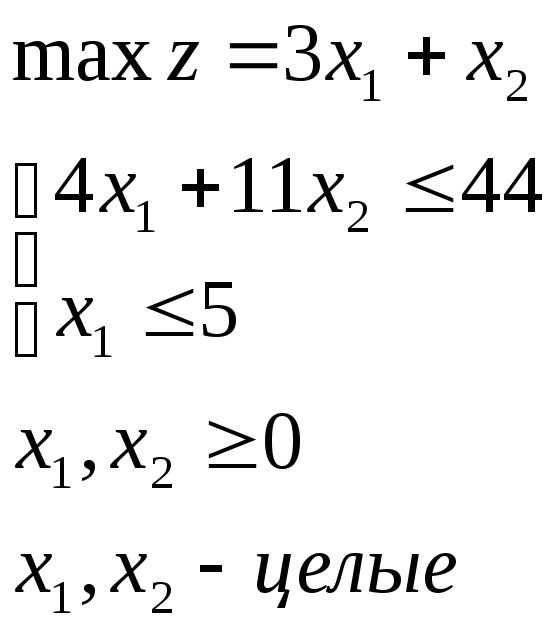
Ответ:

№8

Ответ:

№9

Ответ:

Практическое занятие №7 Тема «Транспортная задача»

В пунктах А₁, А₂, А₃ производится однородная продукция в количествах а₁, а₂, а₃ единиц. Готовая продукция поставляется в пункты В₁, В₂, В₃, В₄, потребности которых составляют b₁, b₂ , b₃ , b₄ единиц. Стоимости с_ij перевозок единицы продукции из пункта А_i в пункт В_j заданы матрицей . Требуется

1) Составить методом минимального элемента опорный план задачи;

2) Методом потенциалов найти план перевозок продукции, при котором минимизируются суммарные затраты по ее доставке потребителям;

3) Вычислить суммарные затраты.

№1 а₁=500 а₂=200 а₃=600 b₁=250 b₂=150 b₃=350 b₄=250

№2 а₁=500 а₂=900 а₃=100 b₁=200 b₂=650 b₃=150 b₄=300

№3 а₁=450 а₂=200 а₃=350 b₁=150 b₂=300 b₃=50 b₄=400

№4 а₁=750 а₂=200 а₃=550 b₁=450 b₂=300 b₃=350 b₄=250

Практическое занятие №8

Тема «Нелинейное программирование.

Решение задач нелинейного программирования

методом множителей Лагранжа»

Найти условные экстремумы функций методом Лагранжа

№1 при условии

Ответ:=2,77 в точке () или (1,38; 0,92).

№2 при условии ,

Ответ:=17278 в точке (91;89).

№3 при условии

Ответ: =0,6 в точке (0,83; 0,55), =-0,6 в точке (-0,83; -0,55).

№4 при условии ,

№5 при условии

№6 при условии

№7 при условии

Ответ: =9 в точке (1;-2;2) , =-9 в точке (-1;2;-2).

Практическое занятие №9

Тема «Нелинейное программирование.

Решение задач нелинейного программирования с помощью

теоремы Куна-Таккера»

Найти наибольшее и наименьше значения функции при заданных ограничениях.

№1 , при наличии ограничений

№2 , при наличии ограничений

№3 , при наличии ограничений

№4 , при наличии ограничений

№5 , при наличии ограничений

№6 , при наличии ограничений

Практическое занятие№10

Тема «Элементы теории матричных игр.

Решение матричных игр в чистых стратегиях»

№1 Участники парной игры независимо друг от друга могут записать одну из цифр: 3, 5 или 8. Если разность между цифрами, записанными игроками А и В, окажется положительной, то игрок А выигрывает столько очков, какова получившаяся разность; если разность будет отрицательной , то соответствующее количество очков выигрывает игрок В; если же разность окажется равной нулю, то и выигрыш игроков будет равен нулю. Составить платежную матрицу, найти нижнюю и верхнюю чистые цены игры, максиминную и минимаксную стратегии игроков.

Ответ: α=β=0

№2 Игроки А и В записывают цифры 1 и 2. Игра состоит в том, что кроме цифры 1 или 2 каждый игрок записывает еще и ту цифру, которую, по его мнению, записал партнер. Если оба игрока угадали или оба ошиблись, то партия заканчивается вничью; если же угадал только один, то он получает столько очков, какова сумма записанных им цифр. Составить платежную матрицу, найти нижнюю и верхнюю чистые цены игры, максиминную и минимаксную стратегии игроков.

Ответ: α=-2, β=2.

№3 Игрок А может записать одну из цифр: 2, 4 либо 7; игрок В может записать 1, 3, 4 либо 8. Если обе цифры окажутся одинаковой четности, то игрок А получает столько очков какова сумма записанных цифр; если разной четности – то очки достаются игроку В. Составить платежную матрицу, найти нижнюю и верхнюю чистые цены игры, максиминную и минимаксную стратегии игроков.

Ответ: α=-5, β=8.

№4 Для игр, заданных следующими платежным матрицами, найти нижнюю и верхнюю чистые цены, максиминную и минимаксную стратегии игроков, установить наличие седловых элементов в платежных матрицах (в последнем случае найти решение игры):

а) б) в) г)

д) е)

№5 Выполнить возможные упрощения платежных матриц

а) б)

№ 6 Выполнить возможные упрощения матриц в №4.

№7 Упростить следующие платежные матрицы

а) б) в)