Генезис моделей

Существуют различные виды организации моделей.

1) В первую очередь они зависят от способа организации выборки. Например, расходы от доходов. Можно сформировать ось абсцисс, например, разложить их по уровням доходов таким образом, чтобы в группах было приблизительно равное представительство.

Другая схема - случайное извлечение некоторого набора хозяйств, не ранжируя по уровням дохода.

Итак, стохастичность и нестохастичность определяются способом организации.

2) Возможен вариант уравнения с распределенными лагами: ;

3) формирование системы одновременных уравнений, например, при формировании модели национальной экономики. В правой части экзогенные и эндогенные переменные;

4) еще один вариант модели - в правой части только экзогенные переменные, но они измеряются с ошибкой, при этом сами они могут быть не стохастическими изначально.

Пример.

Пусть y - удельное потребление определенного вида оваров и услуг, i - номер домашнего хозяйства, - среднедушевой доход.

.

Среднедушевой доход практически всегда недостоверен.

Поэтому в подобных моделях чаще всего используется показатель среднедушевого расхода: . При этом . Таким образом, . Изначально, если x - случайная, то .

Тогда, .

.

,

.

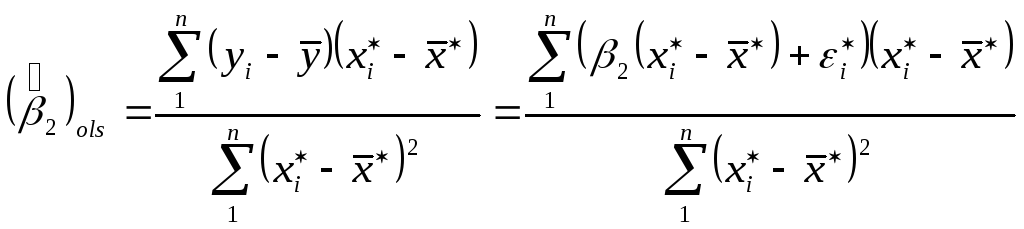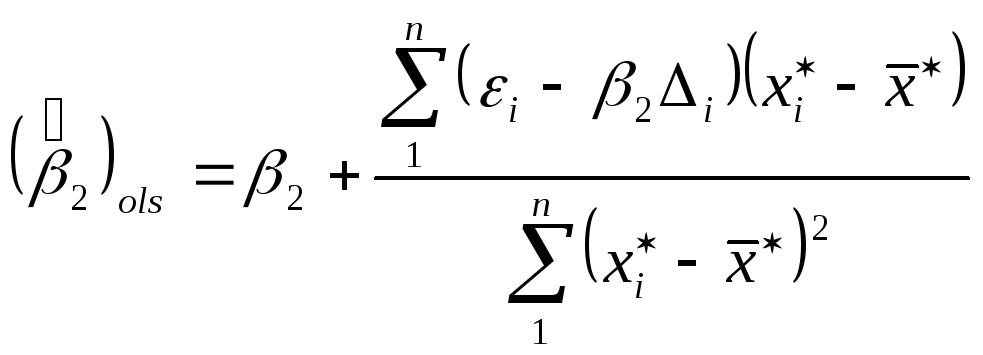Рассмотрим предел по вероятности:

.

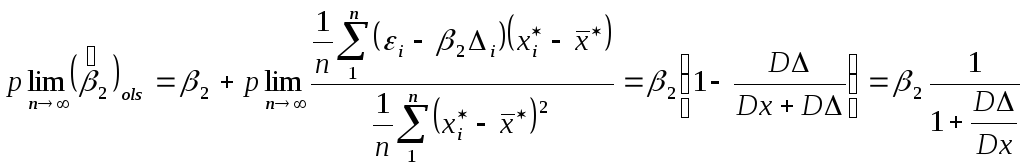Из формулы видно, что возникает неустранимое смещение, что оценка смещенная и несостоятельная.

Если , то использование оценок МНК удовлетворяет требуемой точности.

Но все-таки они перестают быть несмещенными и состоятельными.

Общая схема.

Возможны два случая: 1) взаимная некоррелируемость стохастических предикторов с остатками;

2) коррелированность.

. Для интерпретации: все выводы основываются на кокретной выборке.

, - условия гомоскедастичности и некоррелированности.

Ранг с вероятностью 1.

,

, .

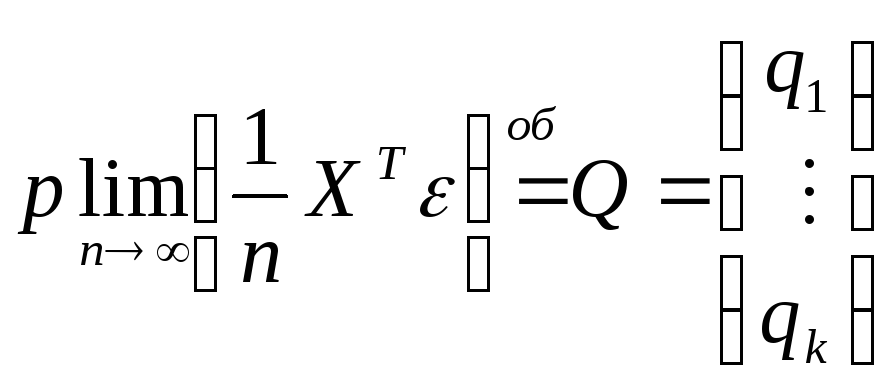Проанализируем оценку МНК в общем случае.

.

.

Если предикаты некоррелируют с, то . В этом случае МНК оценка является несмещенной.

Если в условном случае

,

.

МНК оценка не смещена и условно, и безусловно.

При фиксированной матрице наблюдений, имеем:

.

В классе линейных оценок по y наилучшими будут оценки , где 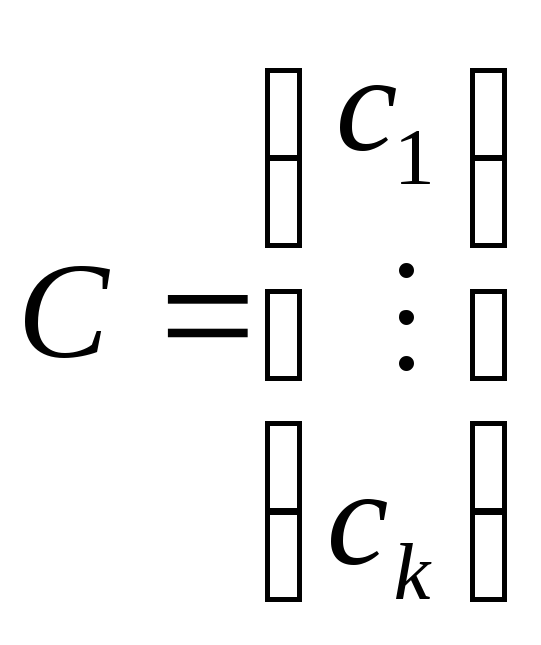- вектор-столбец коэффициентов, в смысле квадрата ошибки.

Свойство оптимальности по теореме Гаусса-Маркова сохраняется:

.

Рассмотрим второй случай: когда коррелируют с , тогда , оценки перестают быть состоятельными. Для этого вводится аппарат инструментальных переменных.

.

Допустим, что только одна переменная коррелирована, т.е. .

Тогда обозначим элемент обратной матрицы , тогда очевидно в формуле получим:

,

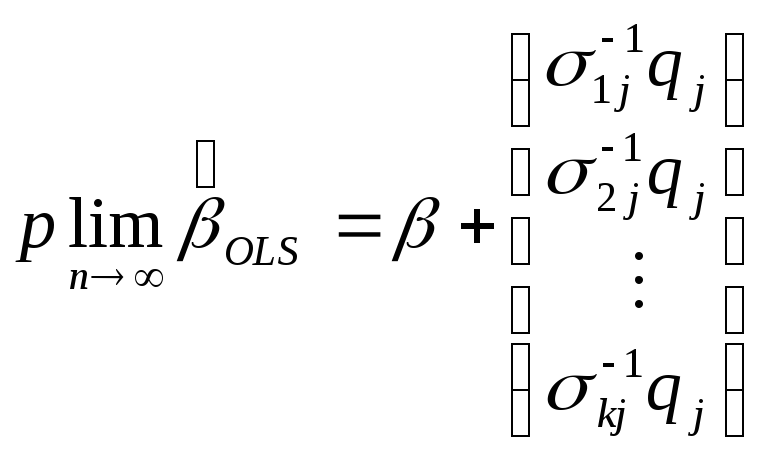тогда все коэффициенты регрессии могут оказаться несостоятельными и смещенными, т.е. метод наименьших квадратов не работает.

Применят метод инструментальных переменных. Чтсло этих переменных должно быть больше либо равно k. Рассмотрим случай равенства.

Требования:

1. часть исходных предикторов - которые слабо коррелируют с остатками;

дополнительные переменные, поддающиеся измерению на тех же объектах (или в те же моменты времени);

искусственно вуеденные переменные - переменные метки.

2. Инструментальные переменные некоррелированы с .

3. - положительно определенная

Каждый из предикторов, которые не вошли в инструментальные, заменить на инструментальные переменные, но так, чтобы новая переменная не коррелировала с остатками.

,

- матрица наблюдений инструментальных переменных.

,

,

- ковариационная матрица инструментальных переменных с точностью до центрирования.

Вместо МНК-оценки предлагается использовать следующую:

.

Утверждается, что эта оценка является состоятельной, условно несмещенной при фиксированных матрицах .

.

В данной формуле только один недостаток - неизвестна , мы имеем только ее оценку:

.

.

Проверка состоятельности:

1. , множитель 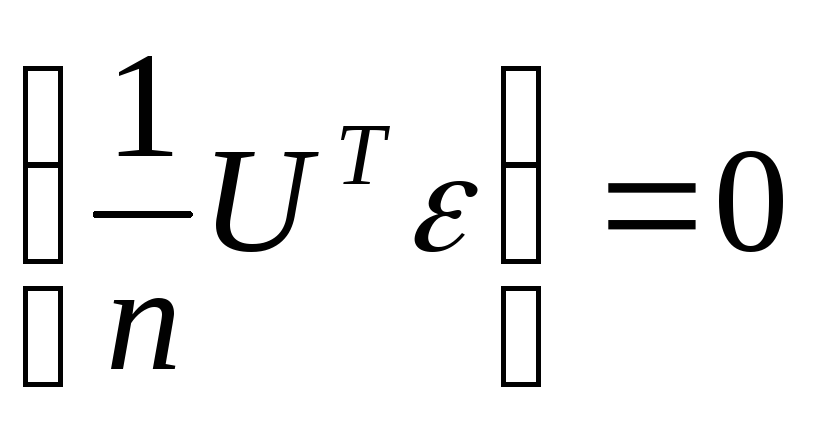в силу некоррелированности.

2. Условная несмещенность - происходит усреднение при условии фиксированных .

3. Вычисляется ковариационная матрица.

Рассмотрим случай парной регрессии.

,

.

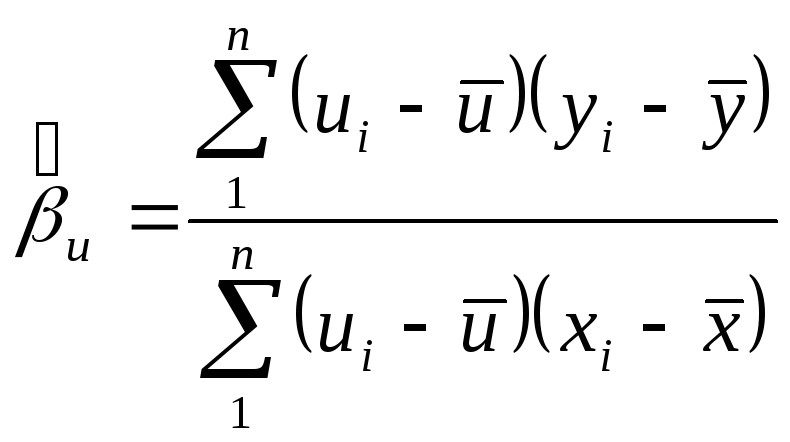Здесь - парный коэффициент корреляции. Необходимо добиться наибольшей корреляции.

Введение переменных меток

Пример.

Рассмотрим задачу о расходах и доходах.

Например, - объявленный доход.

В этом случае, коррелирует с , но нет оснований утверждать, что он коррелирует с остатками .

Первоначально было предложено разбить все наблюдения на два облака. Найти центры тяжести и провести через них прямую.

Согласно Вальда:

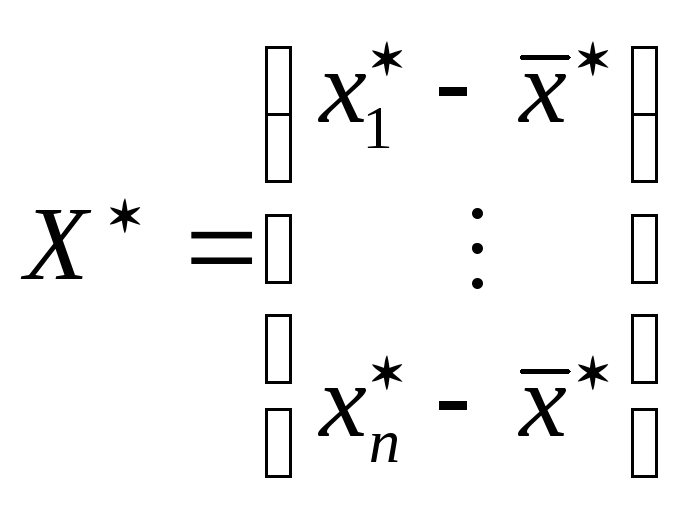и - центрированы, тогда

При таком определении

.

Есть обощение этого подхода в Айвазяне.