Геометрическая структура лага

, где . Предполагаем, что длина лага достаточно велика. Определим c: , , 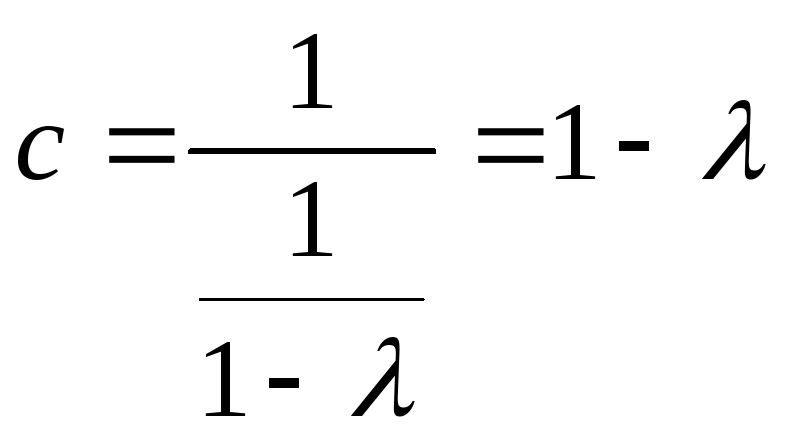тогда .

Итак модель принимает вид:

.

В данной модели имеем четыре параметра для оценивания: .

Преобразуем имеющуюся модель. Для этого выпишем следующее равенство:

.

Домножим уравнение на и вычтем из предыдущего:

,

.

Уравнение упрощается, но

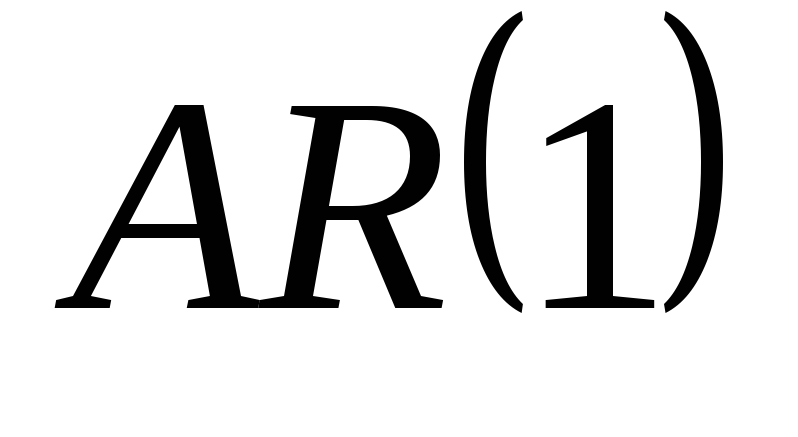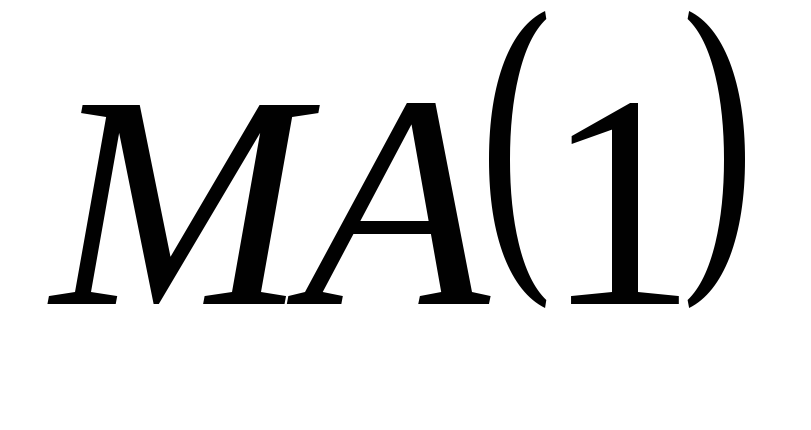1. портится остаток, в первом случае был , а во втором случае - скользящего среднего первого порядка.

2. Появляется стохастическая переменная и она может быть зависима с остатком.

В модели два предиктора и четыре параметра оценки.

Модель 1.

Модель частичной корректировки или частичного приспособления.

Пусть и связаны линейным регрессионным соотношением. Пусть существует , т.е. . Например, желаемая величина основных фондов. А в этой ситуации - выпуск, объем произведенной продукции (на самом деле в логарифмах).

Реальное же состояние модели:

.

В общей схеме добавляется случайный остаток. При близкой настройке . Для построения модели получаем следующую зависимость:

.

Можно подставлять в этом же виде, получим модель с распределенными лагами.

Пример 1.1.

Задача моделирования оптимальных объемов предложения.

- уровень продаж;

- оптимальный с точки зрения равновесия объем предложения;

- реальный объем.

Постулируется, что . Выписывается функция потерь от необходимой настройки:

,

здесь - стоимость перенастройки производства.

Минимизируем функцию потерь:

,

.

Пример 1.2.

Регулирование выплаты дивидендов от прибыли.

- прибыль;

.

Модель 2.

Модель адаптивных ожиданий.

Предполагается, что .

- поведение зависит от значения показателя в будущем, прогноз делается в момент времени t.

. Иначе, .

. Домножим на и вычтем из уравнения для момента времени t, получим:

.

Таким образом, получаем уравнение той же структуры.

Пример 2.1.

Задачи с инфляцией.

Модель гиперинфляции Кагана.

, - индекс изменения денег в обращении, - индекс потребительских цен. - уровень инфляции. .

Подбор параметра

Пусть имеется совокупность исходных данных . Выборка разбивается на две группы: обучающая и экзаменующая.

Например, кваратальные данные за 9 лет. 6 лет - обучающая, и 3 года - экзаменующая.

Выбирается сетка значений для от 0 до 1 с шагом 0,01 или 0,05 в зависимости от характера исследования. Строится решение для каждого по обучающей выборке.

Следующим шагом выбирается критерий качества модели. Например:

• для прогноза - по экзаменующей выборке;

• для структурных - критерий точности - сравнение нескольких методов и т.д.

Полиномиальная лаговая структура (Алмонд)

, k - глубина лага

,

,

,

Подставляем в модель, .

Получим:

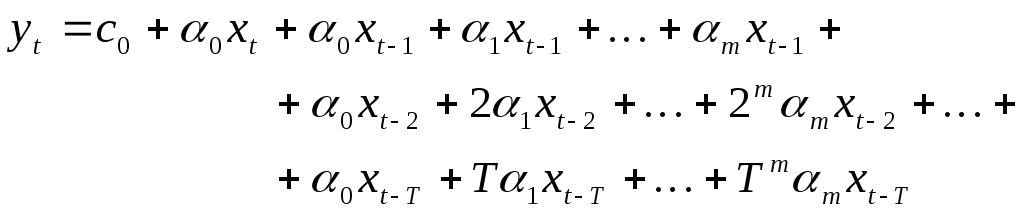
Группируем и суммируем:

.

На выходе получим оценки параметров .

При вероятностной интерпретации (например, для биномиального закона)

.
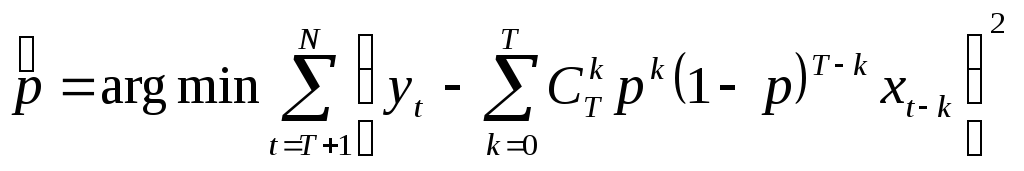