Тесты на гетероскедастичность

1. Тест White

Например, рассматривается регрессия: .

1. Применяем обобщенный метод наименьших квадратов.

2. Оцениваем вспомогательную регрессию:

.

Получаем вектор коэффициентов .

3. Оцениваем гипотезу 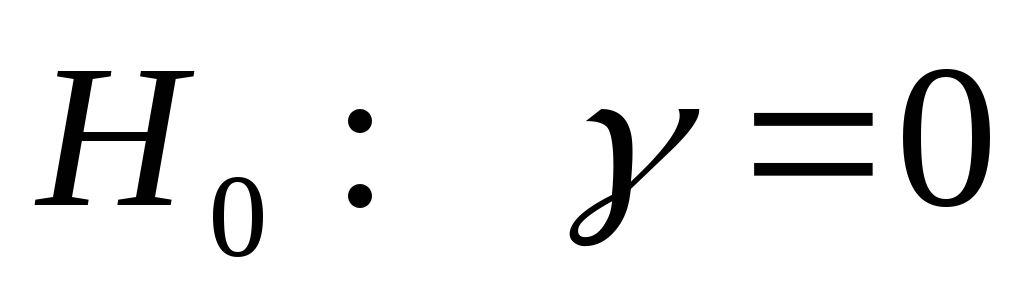. Можно использовать статистику Фишера. Лучше использовать асимптотически правильный тест. Вайт предложил следующий:

,

где q – количество регрессоров (в нашем примере 5). Плюсом этого теста является то, что он очень общий. А отрицательная сторона в том, что его мощность ниже, чем у других. Следовательно можно пропустить гетероскедастичность.

2. Тест Годфельд-Куандта

Здесь тестируется альтернативная гипотеза . Т.е. дисперсия растет с ростом регрессоров. Для этого все наблюдения упорядочиваются по x. Выбираем наблюдений вверх и вниз от середины. Далее эти наблюдения выбрасываются из рассмотрения. Остаются две группы наблюдений: верхняя с маленьким среднеквадратичным отклонением и нижняя с большим. Берем и вычисляем для каждой группы:

При этом известно, что ESS имеет распределение . Рассмотрим статистику:

.

Независимость достигается за счет независимости наблюдений. Здесь работает односторонняя альтернатива, если очень большое значение, то отвергаем нулевую гипотезу.

Проблемой является количество d. От этого зависит мощность теста. Эмпирически выбирают . Этот тест работает только для одной переменной.

3. Тест Бреуш –Пагана (Breush, Pagan)

В качестве альтернативной гипотезы принимается: . Для тестирования выполняются следующие этапы:

1) осуществляется регрессия обычным методом наименьших квадратов. В результате получаются оценки . Тогда можно получить оценку дисперсии: .

2) осуществляется вспомогательная регрессия . В результате получаем RSS. При выполнении нулевой гипотезы: . Здесь p – количество переменных z. Таким образом, если RSS маленькое, то принимается нулевая гипотеза. Для всех тестов нулевая гипотеза – наличие гомоскедастичности.

Другая формулировка этого же теста приводит к изменению второго этапа. Осуществляется регрессия: . При этом величина . Принятие гипотез аналогично предыдущему случаю.

Достоинство этого теста: готовый ответ при отвержении нулевой гипотезы. Недостаток – не знание формулы вспомогательной регрессии.

Автокорреляция остатков

В классической модели предикторы не случайны и определяют вид матрицы ковариаций. Рассмотрим:

Первое предположение – автокоррелированность остатков;

Второе предположение – отказ от неслучайности предикторов;

Третье предположение – предположение о дискретности модели (отказ от количественности модели;

Четвертое предположение – использование пространственны данных (панельные данные);

Далее: - отказ от линейности и по предикторам и по оцениваемым параметрам;

- оценивание модели по цензурированным выборкам.

Вернемся к классической модели:

.

k – число предикторов, включая свободный член.

- либо известна, либо оцениваема по исходным данным. Матрица X является матрицей полного ранга по столбцам. Применяя обобщенный метод наименьших квадратов, получим:

.

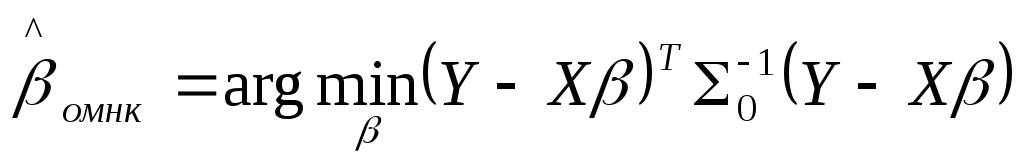Далее решаем оптимизационную задачу. Получаем:

.

Тогда оценка матрицы ковариаций будет иметь вид:

.

.

Вся сложность данного метода заключается в матрице . В некоторых случаях она состоятельно оценивается.

Оценки, полученные методом наименьших квадратов остаются состоятельными, при увеличении числа наблюдений стремятся к нужным. Но эти оценки не будут эффективными, есть более предпочтительные с точки зрения точности оценивания.

Итак, рассмотрим модель:

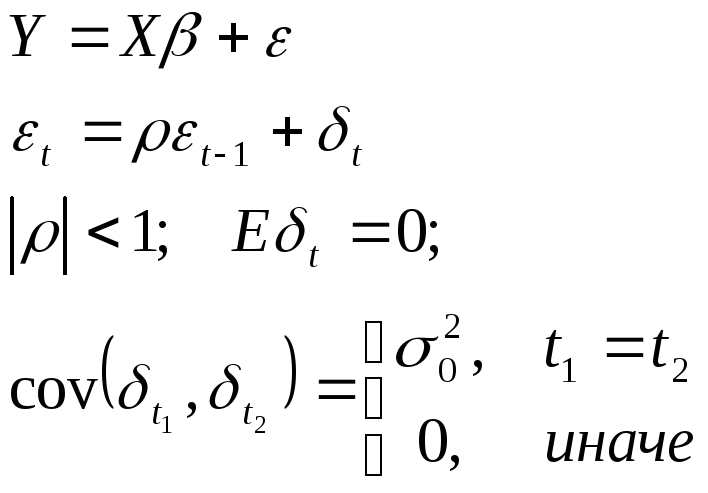
Чаще всего такая модель имеет место во временных рядах.

Необходимо найти математичекое ожидание и матрицу ковариаций. Тогда можно перейти к обобщенной модели:

1)

.

(попарные произведения можно игнорировать в силу некоррелированности).

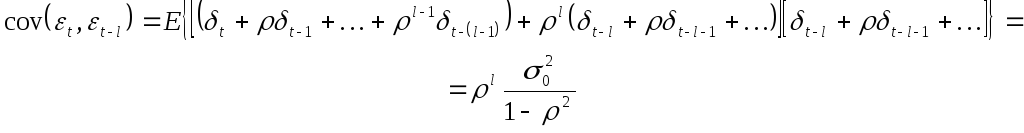
Следует из определения ковариации и того, что математическое ожидание равно нулю..

Тогда, , где , ,

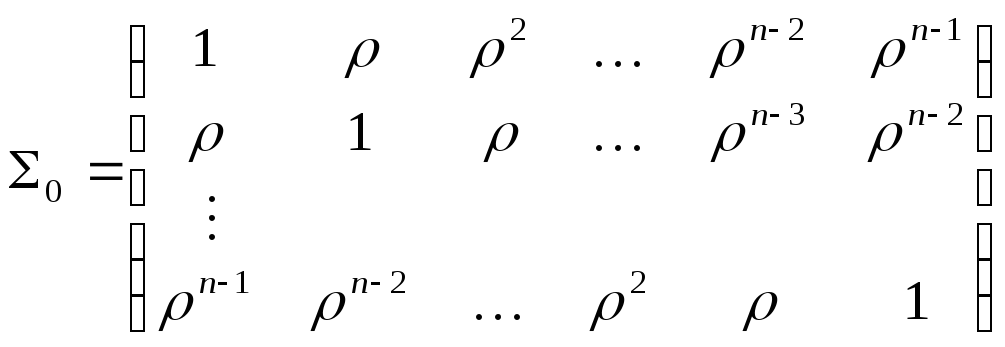- коэффициент корреляции. Таким образом возникает проблема оценивания параметра и его интерпретации.

2) Оценивание параметров модели.

Опишем процедуру Кохрейна-Оркатта. Она является итерационной.

Первым приближением являются оценки, получаемый методом наименьших квадратов . Далее строим первое приближение для невязок: . Исходя из это приближения оцениваем . . Отсюда получаем оценки для в явном виде . Строим матрицу ковариаций . Далее строим оценки обобщенного метода наименьших квадратов .

Далее строим следующее приближение: , и далее повторяем все шаги до достижения нужной точности. Этот метод требует правило останова.

Сходимость метода можно посмотреть в учебнике Айвазяна.

На выходе получим следующий набор параметров:

,

,

.

3) Оценки по методу Neway-West.

Рассматриваются оценки метода наименьших квадратов. Необходимо оценить матрицу ковариаций. Делаются следующие два допущения:

1. Гомоскедастичность не требуется, т.е. , т.е. дисперсия не обязательна постоянна.

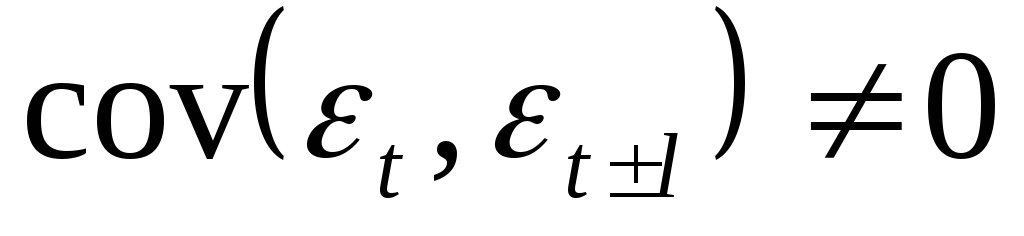2. при всех 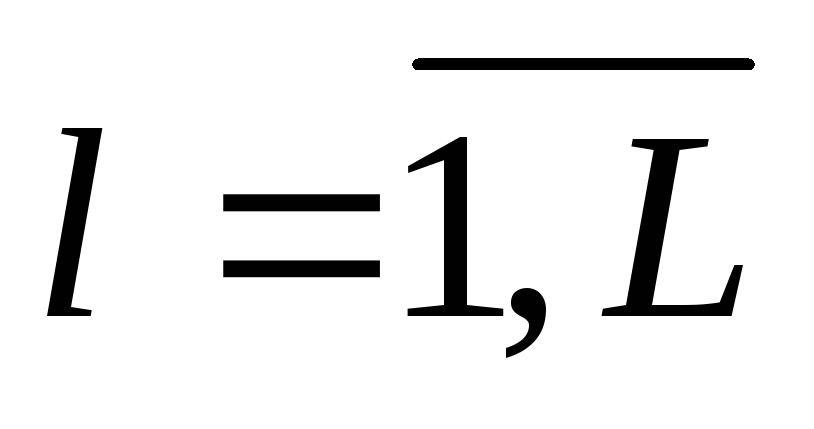, а при 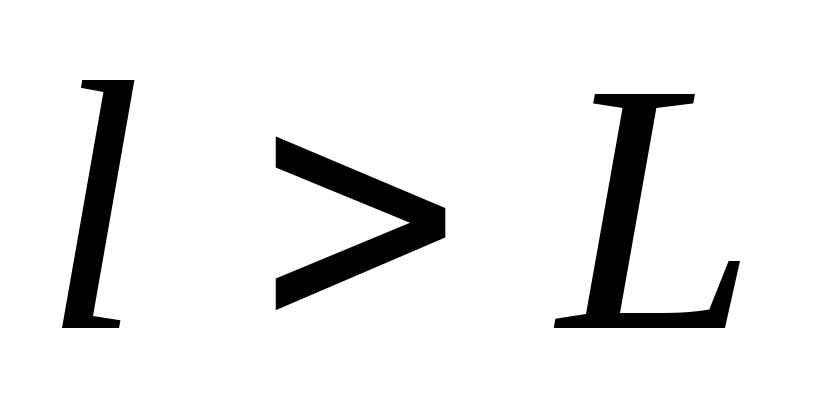ковариации равны 0. В нашем случае это условие выполняется.

,

- оценки по методу наименьших квадратов.

В данной формуле проблемным является нахождение весов. Существует несколько методов. Например, метод Барлета: