Различие между остатками регрессии и ошибками

1) , здесь - ошибки.

2) , e – остатки.

В силу случайности и , e является случайным вектором. Обычно говорят, что e является оценкой . При этом, ошибки являются ненаблюдаемой величиной, а остатки – наблюдаемой.

Мультиколлинеарность

Рассмотрим модель регрессии:

X – матрица данных, Y – столбец, - вектор случайных значений. Тогда оценка коэффициентов регрессии:

,

точность оценки рассчитывается по формуле:

.

При описании модели различают два вида мультиколлинеарности:

1. чистая или полная мультиколлинеарность: ранг матрицы X не полный по столбцам, т.е. меньше k, или 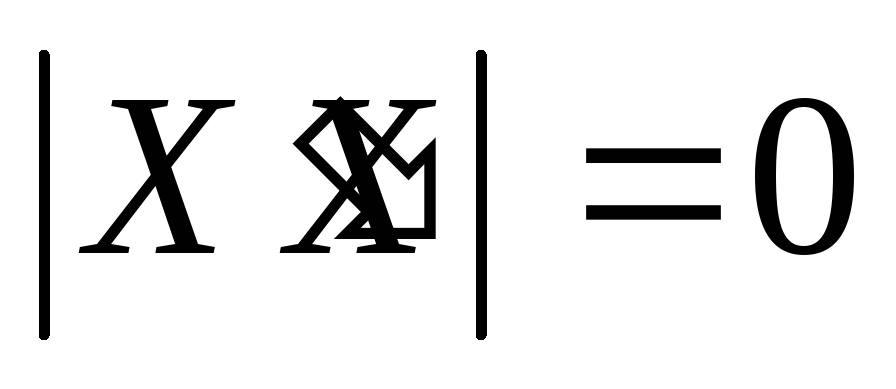. В этом случае по свойству определителей имеем чистую линейную зависимость между строками или столбцами.

2. Частичная или практическая мультиколлинеарность, т.е. матрица слабо обусловлена, т.е. 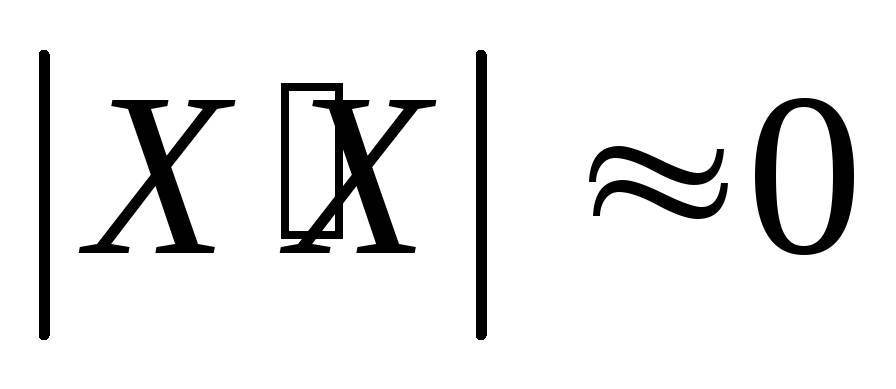, таким образом, определитель соизмерим с ошибкой измерения.

Возможны домодельные и постмодельные признаки мультиколлинераности:

домодельные	(i) или после подсчета собственных чисел матрицы и вычисления числа обусловленности æ=.
	(ii) корреляционная матрица со значениями от 0,7 до 1
	(iii) подсчет коэффициентов детерминации по всем за исключением одной переменной, и при этом близость хотя бы одного коэффициента к 1
	(i4) неустойчивость коэффициентов регрессии к варьированию исходных данных.
постмодельные	(i5) нельзя интерпретировать, коэффициенты, противоречат здравому смыслу

Например, если модель имеет вид: , и , между переменными почти линейная связь. Тогда модель можно записать в одном из видов:

,

.

Итак, эти три модели одинаковы («неустойчивость»).

По этой модели возможно прогнозирование, но точность оценки «расползается». А в структурном плане, т.е. экономической интерпретации доверять нельзя.

Одно из направлений борьбы с мультиколлинеарностью - переход к смещенному оцениванию (регуляризация).

Примером могут служить ridge-оценки (гребневые оценки). Т.е. оценку параметра регрессии заменяем оценкой вида:

Идея отказа от несмещенности состоит в следующем:

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются не интерпретируемыми.

Пример. Рассмотрим регрессию себестоимости единицы продукции (руб., y) от заработной платы работника (руб., x) и производительности его труда (единиц в час, z):

.

Коэффициент регрессии при переменной z показывает, что с ростом производительности труда на 1 ед. себестоимость единицы продукции снижается в среднем на 10 руб. при постоянном уровне оплаты труда. Вместе с тем параметр при x нельзя интерпретировать как снижение себестоимости единицы продукции за счет роста заработной платы. Отрицательное значение коэффициента регрессии при переменной x в данном случае обусловлено высокой корреляцией между x и z (). Поэтому роста заработной платы при неизменности производительности труда не может быть (если не учитывать инфляцию).

Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента.

Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют t-­статистики для параметров регрессии.

Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если .

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. В этом случае вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих причин:

• затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в чистом виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл;

• оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

Мультиколлинеарность может возникать в силу различных причин. Например, несколько независимых переменных могут иметь общий временной тренд, относительно которого они совершают малые колебания.

Выделим некоторые наиболее характерные признаки мультиколлинеарности:

• Небольшое изменение исходных данных (например, добавление новых наблюдений) приводит к существенному изменению оценок коэффициентов модели.

• Оценки имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой (высокой значение коэффициента детерминации и соответствующей статистики Фишера).

• Оценки коэффициентов имеют неправильные с точки зрения теории знаки или неоправданно большие значения.

При столкновении с проблемой мультиколлинеарности возникает желание отбросить «лишние» независимые переменные, которые, возможно, служат ее причиной. Однако, во-первых, далеко не всегда ясно, какие переменные являются лишними в указанном смысле. Во-вторых, во многих ситуациях удаление какой-либо независимой переменной может значительно отразится на содержательном смысле модели. В-третьих, отбрасывание существенных переменных, которые реально влияют на изучаемую зависимую переменную, приводит к смещенности оценок.

По такой модели удобно прогнозировать, но точность прогнозов невысокая.

Итак, рассмотрим классическую модель в тех же предположения, что и для парной регрессии.

.

Если , то - константа.

Все условия, налагаемее на - те же, что и для парной регрессии. Для вычисления оценок удобно перейти к матрицам. Будем считать, что в задаче имеется k регрессоров.

Направления борьбы с мультиколлинеарностью:

(а) переход к смещенному оцениванию (регуляризация). Например, ridge – оценки (гребневые оценки). Происходит замена исходной оценки на следующую:

.

Идея, на которой основан