2.8. Асинхронный двигатель как объект регулирования

Из структурной схемы (рис.2.10) следует, что для процессов в роторе в качестве входных переменных можно считать токи статора вдоль осей координат x и y. В этом случае процессы описываются уравнениями (2.58), которые в операторной форме записи приводятся к виду:

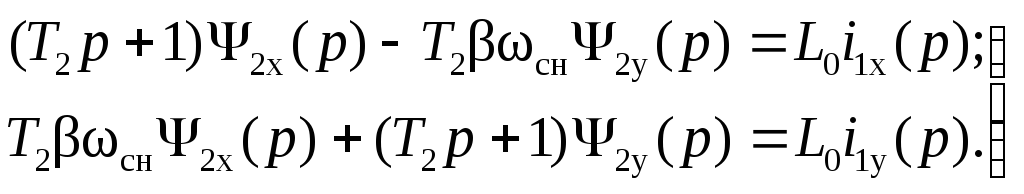(2.70)

Решая относительно потокосцеплений, находим:

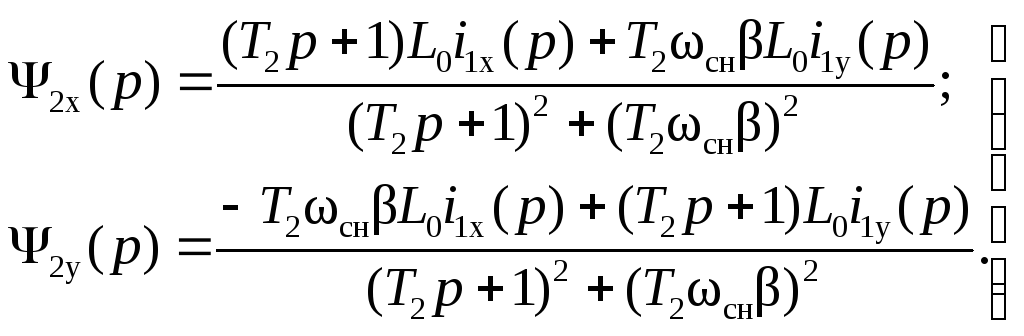(2.71)

При вычислении электромагнитного момента воспользуемся одним из уравнений в (2.48)

.

С учётом (2.68) после группировки отдельных переменных, получим:

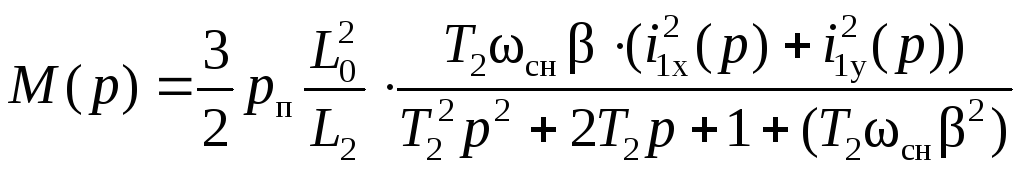, или

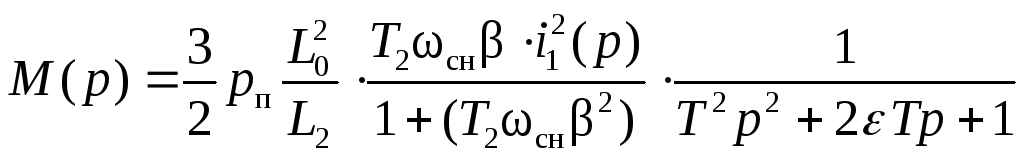(2.72)

Введём понятие передаточной функции

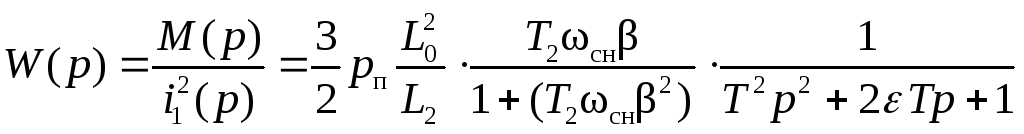.(2.73)

Постоянная времени Т и коэффициент демпфирования зависят от абсолютного скольжения и от постоянной времени ротора:

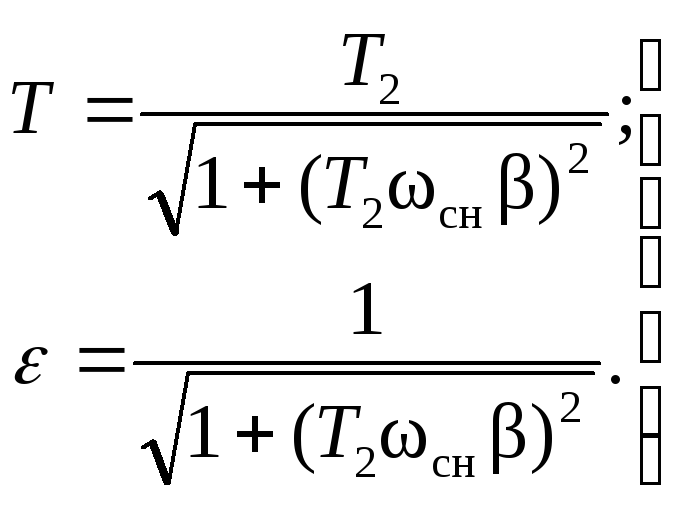(2.74)

Характеристическое уравнение имеет два сопряжённых комплексных корня

,

где коэффициент затухания и угловая частота колебаний рассчитываются по формулам:

(2.75)

С учётом (2.74) получим:

(2.76)

Период колебаний

(2.77)

Частота собственных колебаний совпадает с частотой переменных в роторе

(2.78)

Из приведенных уравнений видно, что электромагнитные процессы имеют колебательный характер, время затухания колебаний зависит от постоянной времени ротора (2.76), а частота колебаний пропорциональна абсолютному скольжению (2.78).

П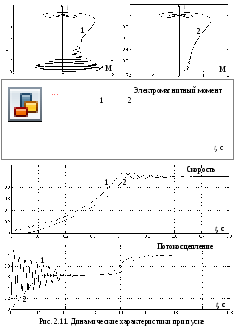 оведение двигателя при пуске характеризуется кривыми на рис. 2.11.

На приведенном рисунке рассматриваются два случая отмеченные цифрами 1 и 2.

В первом случае в момент времени скачком прикладывается номинальное напряжение с частотой 50 Гц.

Во втором случае на отрезке времени 0 < t < 0,1c напряжение меняется по линейному закону, а далее остаётся постоянным и равным номинальному значению. На начальном участке потокосцепление , также как и напряжение, тоже нарастает примерно по линейному закону. Благодаря этому существенно уменьшаются колебания электромагнитного момента возникающие в начальный момент пуска. Устройства, работающие по такому принципу, стали называть устройствами плавного пуска.

Выводы:

1. Асинхронный двигатель представляет собой замкнутую систему (рис. 2.10). Если его рассматривать со стороны приложенного напряжения, то это нелинейное колебательное звено пятого порядка с переменными параметрами. В качестве переменного параметра выступает абсолютное скольжение .

2. Коэффициент затухания колебаний (2.76) α и время затухания процесса зависят от постоянной времени ротора.

3. Частота колебаний (2.78) пропорциональна абсолютному скольжению .

2.9. Модели асинхронного двигателя

Модели бывают математические и виртуальные.

В качестве примера на рис.2.12 приводится математическая модель в системе координат x,y. При составлении модели в качестве исходных данных принималась система дифференциальных уравнений (2.62) – (2.64) и структурная схема (рис.2.10). Модель состоит из двух частей.

В верхней части располагаются элементы, моделирующие процессы в статоре, а в нижней части – процессы в роторе. Вычисление ЭДС, наводимой в статоре, выполняется по (2.60). Модель сложная, содержит большое количество элементов, она повторяет структурную схему и дополнена вычислениями токов ротора и потокосцеплений воздушного зазора. Предусмотрены узлы для задания начальных условий. Параметры указываются в рабочем окне параметров маски.

Виртуальное моделирование [10] стало возможным с появлением современных средств вычислительной техники и пакета специализированных программ типа Matlab. Модель можно составить с помощью схем замещения на рис.2.6.

Наиболее простой является модель в системе координат a, b (рис.2.13)

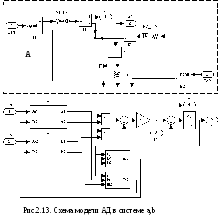
Модель содержит виртуальную часть и математическую.

В виртуальной части для каждой фазы взята отдельная схема замещения. В пространстве эти схемы располагаются по двум взаимноортогональным осям и .

Модель одной фазы показана в раскрытом виде. В ней на вход поступает напряжение: . На вход второй фазы подаётся напряжение .

Для вычисления электромагнитного момента достаточно взять в каждой фазе по два тока

.

Дополнительные ЭДС по осям a, b вычисляются по формулам:

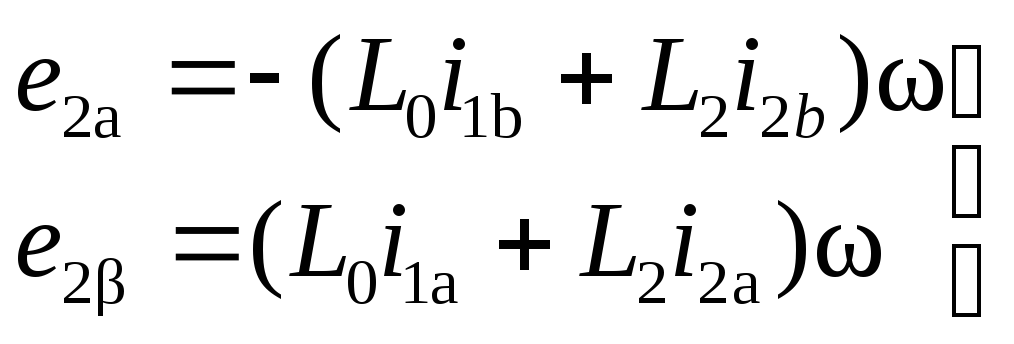
Е сли модель поместить в “черный ящик”, то она принимает компактный вид (рис.2.14).

Напряжение к двигателю поступает от источника синусоидального напряжения, у которого можно регулировать амплитуду, частоту и фазу выходного напряжения, его модель приводится на рис.2.15.

Модель 3-х фазной машины (рис.2.16) содержит три блока со схемами замещения для каждой фазы. От ранее рассмотренной модели эта модель отличается наличием прямых и обратных координатных преобразователей , и .

Модель 2-х фазной машины в системе координат , приводится на рис.2.17.

Рис.2.17. Модель АД в системе координат

Добавочные ЭДС вводятся в статор и ротор. Они вычисляются по формулам:

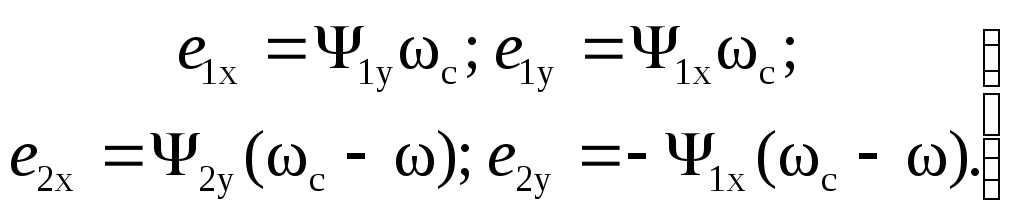
Электромагнитный момент вычисляется по формуле

.

Если взять виртуальную часть модели и сравнить с виртуальной частью модели в системе координат , то по внешнему виду они совпадают. Отличие состоит в том, что здесь в статор вводится дополнительная ЭДС. Эта особенность придаёт модели новые свойства.

Так как система координат и пространственный вектор напряжения вращаются с одной скоростью , то в этой системе координат вектор напряжения можно представить в следующих формах записи:

.

Здесь действительная ось комплексной плоскости совмещена с осью х.

Напряжения , поступающие на вход модели, не содержат синусоидальных функций, это напряжения для электрических цепей постоянного тока.

Таким образом, при анализе процессов в системе координат х, у приходится оперировать с переменными для электрических цепей постоянного тока. Процессы представляются в более наглядном виде, управлять такими процессами проще. Это одно из достоинств модели в системе координат х, у.

Виртуальная часть рассмотренных моделей содержит активные сопротивления и индуктивности. Так как параметры этих элементов в общем случае могут быть переменными и нелинейными, то при моделировании возникает потребность в составлении их моделей (рис.2.18).

Модель активного сопротивления (а) содержит измеритель тока в электрической цепи, безынерционный элемент R и источник ЭДС. Здесь моделируется напряжение на активном сопротивлении для участка электрической цепи, выходная переменная описывается равенством

.

Модель индуктивности (б) описывает напряжение на участке электрической цепи содержащей индуктивность

.

Операция дифференцирования выполняется с помощью реального дифференцирующего звена. Малая постоянная времени этого звена характеризует точность моделирования.

Модель нелинейной индуктивности (в) отличается от ранее рассмотренной модели наличием нелинейного звена HZ. С помощью этой модели удобно учитывать насыщение магнитной системы. Здесь напряжение для рассматриваемого участка описывается равенством, которое описывает явление электромагнитной индукции (1.1)

.

Система замкнутая, ток протекает под действием приложенного напряжения. Ток измеряется и его модуль формируется нелинейным звеном. В качестве нелинейного звена принимается кривая намагничивания . После дифференцирования формируется напряжение на индуктивности. Получается, что потокосцепление становится пропорциональным приложенному напряжению, а ток становится нелинейной функцией от приложенного напряжения. Особенность этого участка элект рической прокомментируем с помощью рис.2.19.

Здесь, в первом квадранте изображена нелинейная функция, состоящая из отрезков двух прямых. Во втором квадранте представлен отрезок синусоидальной функции . Эта кривая пропорциональна приложенному напряжению на индуктивности. В четвёртом квадранте располагается кривая мгновенного тока. При насыщении ток становится несинусоидальным, возрастает его амплитуда, появляются дополнительные составляющие и дополнительные потери, повышающие нагрев обмотки.

Так как виртуальные модели состоят из обмоток расположенных в пространстве, то при необходимости можно проводить исследование процессов с учётом магнитной и электрической несимметрии, если таковые имеются.

Характеристику “вход-выход ” нелинейного звена можно представлять не только в графическом, но и в аналитическом виде. По этому же принципу составляется модель нелинейного сопротивления.

85