2.5. Процесс преобразования энергии и электромагнитный момент
Асинхронный двигатель потребляет от источника питания активную и реактивную мощность.
Активную мощность можно записать в виде скалярного произведения вектора напряжения на вектор тока
.
(2.43)
Напомним, что здесь
и
.
Реактивная мощность идёт на создание главного поля и полей рассеяния
.
Важным энергетическим показателем является коэффициент мощности
.
Активная мощность состоит из двух составляющих
.
Первая составляющая представляет собой мощность потерь в активных сопротивлениях статора
.
Разность между
мощностью
и потерями мощности в активных
сопротивлениях статора
принято называть электромагнитной
мощностью
.
Эта мощность через воздушный зазор
передаётся в ротор.
Если в (2-43) напряжение
заменить вектором напряжения за активным
сопротивлением статора
(рис.2.2) , то получим уравнение для
электромагнитной мощности
.
(2.44)
З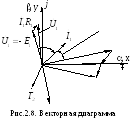
десь
представляет собой угол между векторами
(рис.2.8).
В (2.44) перейдём от
к
,
а затем к
При выполнении операций
с векторами целесообразно пользоваться
одной методикой. Дополнив угол
до
градусов, выполним формальный переход
от скалярного произведения к векторному
произведению
(2.45)
Напомним, что при
вычислении векторного произведения
отсчёт углов производится против часовой
стрелки от первого вектора
ко второму вектору
[11].
Электромагнитная
мощность, проходя через воздушный зазор,
преобразуется в механическую мощность,
и её можно выразить через электромагнитный
момент. Так как поле вращается со
скоростью
,
то можно записать
.
(2.46)
При совместном решении (2.45) и (2.46) находим
(2.47)
Ранее было показано, что процесс преобразования электрической энергии в механическую энергию происходит в пространственной области. В ортогональных системах координат можно выполнять формальный переход от временных векторов к пространственным векторам. Такой переход выполнен в (2.47).
Если от электромагнитной мощности отнять мощность электрических потерь в сопротивлениях ротора, то оставшаяся часть преобразуется в механическую мощность на валу двигателя
;
.
В ряде случаев удобно представлять электромагнитный момент в виде векторного произведения двух других векторов. В этом случае следует записать уравнение связи между этими векторами и перейти от одного вектора к другому.
Потокосцепления связаны уравнениями
,
.
Здесь
,
- полные индуктивности фазы статора и
ротора.
Токи связаны равенством
.
Допустим, что хотим
выразить электромагнитный момент через
потокосцепление
и ток статора
.
Процесс преобразований описывается
равенствами
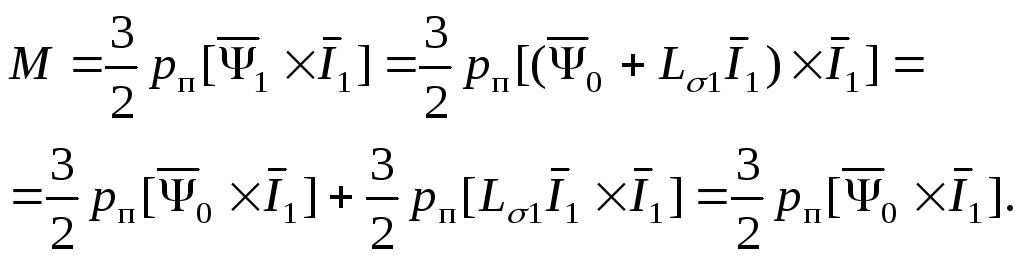
Если эту методику повторить для других векторов, то число уравнений для электромагнитного момента возрастёт. Его можно вычислять с помощью одного из следующих уравнений:
Здесь, в левой части момент представлен в виде векторного произведения двух результирующих векторов. Этими уравнениями можно пользоваться в любой из известных систем координат. В правой части записаны уравнения во вращающейся системе координат “xy”.
Если нужно перейти к
неподвижной системе координат a,
b,
то достаточно изменить лишь символику
для переменных. Символ x
следует заменить символом
,
а символ y
заменить на
.
Так, например уравнение с номером 2 в системах координат x, y и a, b принимает вид
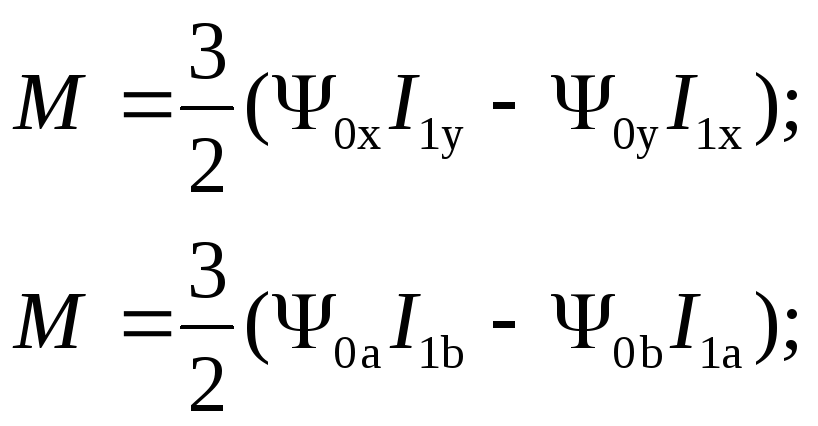
В первом уравнении
вектора
и
не совершают вращательного движения,
они лишь поворачиваются на определённые
углы и меняются по модулю. В вычислениях
электромагнитного момента нет
синусоидальных функций.
Во втором уравнении
эти же вектора совершают вращательное
движение со скоростью
.
Проекции этих векторов меняются по
законам синуса и косинуса и участвуют
в процессе вычисления электромагнитного
момента.
Сам процесс вычислений в разных системах координат имеет принципиальные отличия, а результат вычислений получается одинаковым.
Система координат
удобна для организации процесса
управления объектом и хорошо воспринимается
в процессе анализа отдельных явлений.
Процессы в неподвижных
системах координат
и
максимально приближены к реальным
процессам в электрических цепях
переменного тока.
Выводы:
1. Полезная работа совершается за счёт преобразования активной мощности, потребляемой из сети, в механическую мощность.
2. Реактивная мощность идёт на создание магнитного поля, с помощью которого возникает электромагнитный момент.