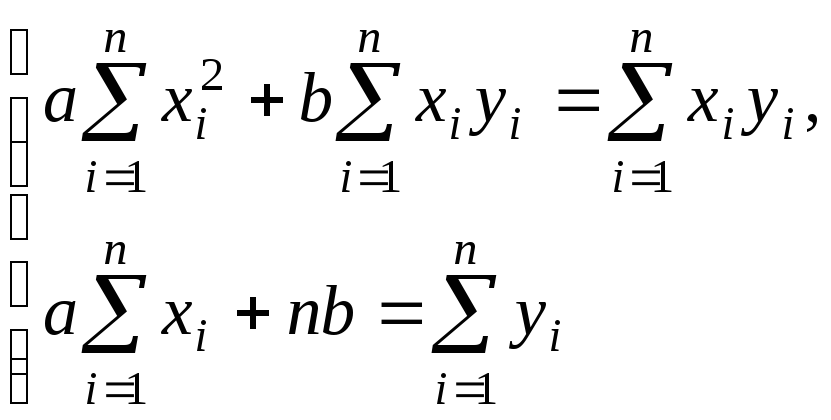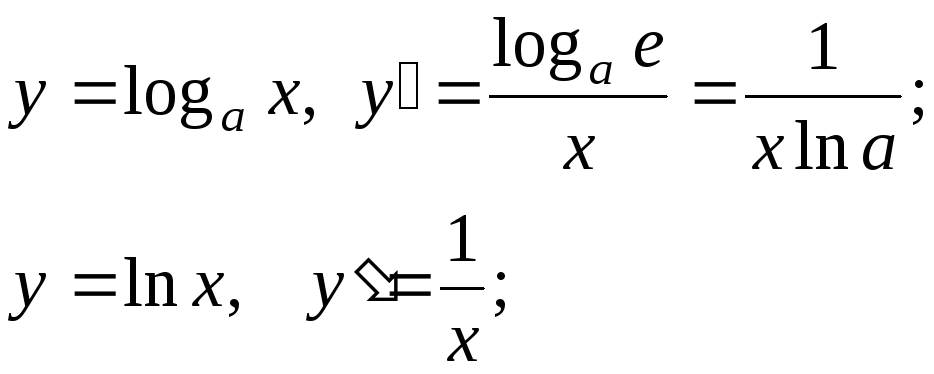Приложение а. Элементарные функции. Преобразование графиков функций
Основные элементарные функции:
-
степенная:
-
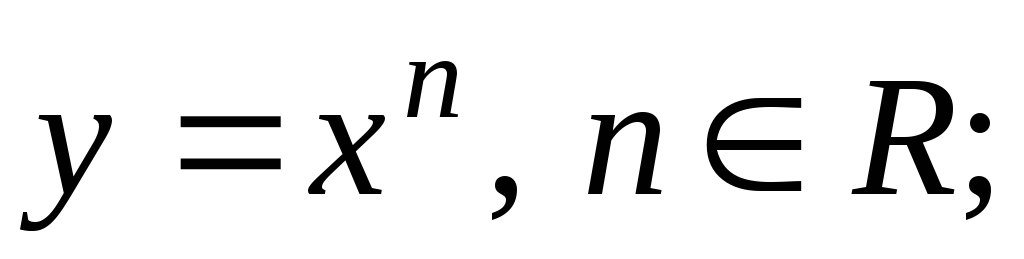
логарифмическая:
-
показательная:
-
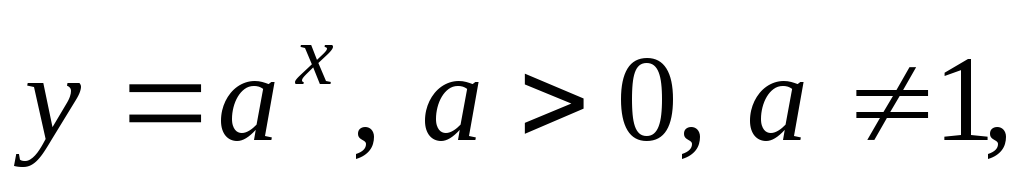
тригонометрические:
-
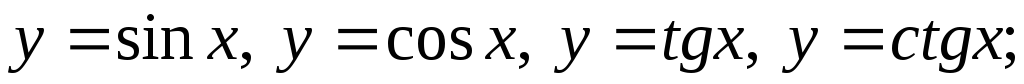
обратные тригонометрические:
Показательные
и логарифмические функции находят
применение в финансовых вычислениях.
Большинство банковских операций состоит
в выдаче денег «в рост» или «под процент».
Наращенный (конечный) капитал
вычисляется по формулам
(1)
или
, (2)
где
-
начальный капитал;
n – период начисления процентов;
i – процентная ставка.
По формуле (1) начисляют простые проценты, по формуле (2) – сложные. В формуле (1) используется линейная зависимость, в формуле (2) – показательная.
Множество
точек плоскости с координатами
называется графиком функции
.
Для построения графиков функций
используют следующие приемы: построение
по точкам; действия с графиками (сложение,
вычитание, умножение на число);
преобразование графика (сдвиг, растяжение
и сжатие по осям). Так, например, если
известен график функции
,
можно построить графики функций:
1)
– сдвиг графика функции
по оси Ox;
2)
– сдвиг графика функции
по оси Oy;
3)
– растяжение или сжатие графика
по оси Ox
4)
– растяжение или сжатие по оси Oy
5)
– график совпадает с графиком
для
и является его симметричным отображением
относительно оси Oy
для
;
6)
– график совпадает с графиком
для
и является его симметричным отображением
относительно оси O,
если
.
Приложение б. Производная
Производной
функции
в точке
(обозначается
или
)
называется предел отношения приращения
функции в этой точке
к приращению аргумента
при
,
если этот предел существует:
.
Операция нахождения производной называется дифференцированием.
Таблица основных производных
|
1)
|
6)
|
|
2)
|
7)
|
|
3)
|
8)
9)
|
|
4)
|
10)
11)
|
|
5)
|
12)
|
;
;
;
;
;
;
;
;
;
.
Правила дифференцирования
1)
;
2)
;
3)
.
Приложение в. Метод наименьших квадратов
В экономической практике часто требуется представить наблюдаемые (измеренные) данные в виде функциональной зависимости. При этом предполагается, что вид функциональной зависимости известен (например, в результате ранее проведенных исследований), и требуется определить только параметры этой зависимости.
Пусть в ходе исследования (например, покупательского спроса) получена следующая таблица, где х – аргумент (цена товара), а у – функция (количество товара):
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
Требуется по этим табличным данным получить функциональную зависимость (кривую спроса). Для оценки вида функциональной зависимости данные таблицы можно представить в виде точек на плоскости.
Допустим,
расположение точек позволяет предположить,
что функциональная зависимость –
линейная:
.
Задача сводится к нахождению таких
значений параметров а и b,
при которых функция
принимает наименьшее значение.
Чтобы
найти прямую, наилучшим образом
согласованную с экспериментальными
данными (
достаточно решить систему уравнений:
