9. Поверхневі процеси. Рівноважний контакт метал-плазма

У попередньому параграфі показано, що поверхневі процеси впливають на величину параметра нерівноважні, який визначає величину зміщення іонізаційної рівноваги. Тому представляє інтерес детально вивчити іонізаційно-рекомбінаційні процеси на поверхні конденсованої частинки.

Розглянемо контакт димова частинка – плазма в наближенні плоскої поверхні. Це означає, що нами приймається припущення про те, що довжина вільного пробігу електронів, іонів і нейтралів багато менше радіусу частинок. Довжина вільного пробігу  у низькотемпературній плазмі визначається концентрацією атомів буферного газу, яка складає при атмосферному тиску 2,710²⁵ м^-3; відповідно 3,310^-7 м. Отже, для частинок розміром більше 1 мкм наближення плоскої поверхні справедливе.

Частинка диму, знаходячись в рівновазі з плазмою, має достатньо високу температуру для того, щоб термоелектронна емісія істотно впливала на іонізаційну рівновагу плазми. Це вперше було знайдено у вуглеводневому полум'ї Сагденом і Трашем .

Модель рівноважної взаємодії частинок диму з плазмою з урахуванням як випромінювання, так і поглинання електронів була запропонована Ейнбіндером. У всіх випадках рівновага на межі частинка диму – плазма зводиться до балансу потоків термоелектронної емісії і зворотного потоку поглинання електронів.

Заряд частинок оксиду кремнію визначається як результат балансу струму електронів

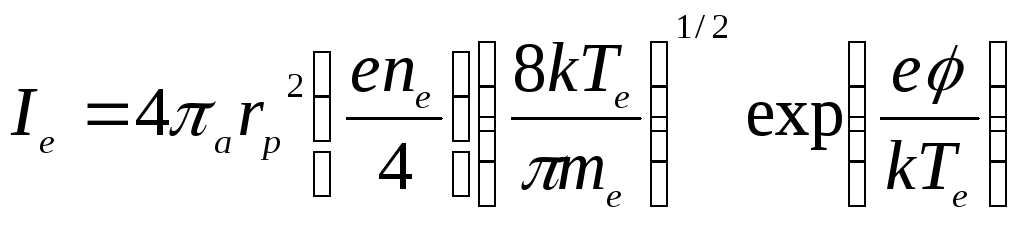
і струму іонів

на поверхню частинки радіусу . В цьому випадку на поверхні частинки відбувається повна рекомбінація електронів і іонів з вірогідністю рівній одиниці. Це дуже велика ідеалізація, оскільки поверхня частинок повинна бути достатньо активною, хоча б за рахунок рівнів Тамма, що утворюються в результаті обриву кристалічних зв’язків. Крім того, якщо термоелектронною емісією можна нехтувати, то іонізацію атомів на поверхні частинок необхідно враховувати, оскільки цей процес визначається емісією дірок з

Термоелектронна емісія визначається тільки роботою виходу і температурою. Робота виходу електрона це енергетичний зазор між рівнем Фермі частинки і рівнем вакууму. В даному випадку заряд частинки змінює роботу виходу. Таке можливе тільки при істотній зміні рівня Фермі в матеріалі частинки, що визначається загальною кількістю вільних електронів і, якщо частинка металева, то для цього необхідна густина заряду на рівні електронів на кубічний метр.

З проведеного аналізу виходить, що на поверхні частинок необхідно враховувати також іонізаційно – рекомбінаційні процеси, які виражаються в рекомбінації іонів і іонізації атомів.

Таким чином, на поверхні конденсованої частинки враховуватимемо наступні потоки:

(а) потік термоелектронної емісії Річардсона – Дешмана:

, (9.1)

де - густина електричного струму в напрямі від частинки в плазму,

- робота виходу електрона з частинки в плазму.

(б) потік поглинання електронів поверхнею частинки:

, (9.2)

де - теплова швидкість електронів,

- поверхнева концентрація електронів:,

- потенціал поверхні.

(в) потік поверхневої рекомбінації іонів:

, (9.3)

де - теплова швидкість іонів,

- поверхнева концентрація іонів:,

- коефіцієнт поверхневої рекомбінації.

(г) потік поверхневої іонізації атомів:

, (9.4)

де - теплова швидкість атомів ();

- поверхнева концентрація атомів;

- концентрація лужної присадки;

- коефіцієнт поверхневої іонізації.

Розглянемо умови протікання в плазмі електричного струму. При відсутності магнітного поля можливі тільки два механізми перенесення заряду в плазмі - дифузія і дрейф в електричному полі. Тому густину струму виразимо у вигляді:

, (9.5)

, (9.6)

де і - рухливості електронів і іонів.

Враховуючи больцмановській розподіл концентрації електронів і іонів, а також той факт, що потенціал, з виразів (9.5) і (9.6) одержимо:

(9.7)

(9.8)

Тут ми врахували, що

,

.

З викладеного виходить, що умовою протікання в плазмі струму є просторовий розподіл електрохімічного потенціалу і параметра нерівноважності, оскільки розподілом в плазмі продуктів згорання можна нехтувати:

. (9.9)

В стані термодинамічної рівноваги контакту метал – плазма рівень електрохімічного потенціалу плазми має постійне значення і співпадає з рівнем Фермі металу, тому струм кожної з компонент звертається в нуль, оскільки дифузійна складова струму компенсується дрейфовою складовою. Отже, на межі розділу фаз в стані рівноваги існує баланс струмів:

, (9.10)

. (9.11)

Енергетична діаграма контакту метал – плазма з урахуванням параметра зміщення іонізаційної рівноваги представлена на рис. 8. Енергетичні рівні і означають нижню межу енергетичного спектру вільних електронів і іонів (рівень валентного електрона атома) відповідно. Вважатимемо актом взаємодії

Рис.8. Енергетичні діаграми контакту метал – плазма.

іона або атома плазми з поверхнею частинки адсорбцію на поверхні, яка супроводжується перенесенням електрона в тому або іншому напрямі з подальшою десорбцією відповідно атома або іона, оскільки це є необхідною умовою іонізаційної рівноваги.

Робота виходу електрона з металу в плазму відрізняється від роботи виходу з металу у вакуум (саме це значення приводиться в довідковій літературі) на величину потенційного бар'єру в плазмі на межі плазма – вакуум. Величина потенційного бар'єру знаходиться з умови амбіполярної дифузії носіїв заряду:

ј. (9.12)

Отже, якщо робота виходу з димової частинки у вакуум є, то робота виходу з частинки в плазму дорівнює:

ј.

Сума потоків (9.10) дозволяє обчислити значення поверхневої концентрації електронів:

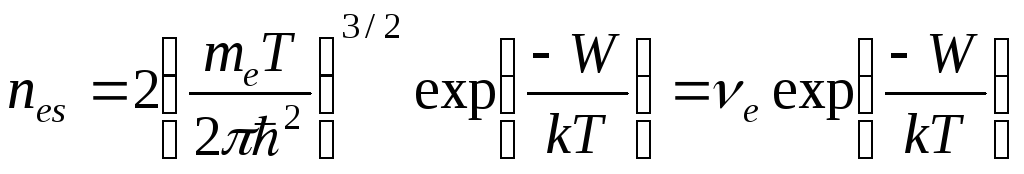, (9.13)

яке може значно перевищувати рівноважне значення в плазмі.

Поверхнева концентрація не залежать від властивостей плазми і визначає тиск насиченої пари електронів біля поверхні частинки в стані термодинамічної рівноваги.

Як видно з діаграм (рис.8), процес іонізації атомів домішки означає перехід валентного електрона з рівня на рівень Фермі металу, для чого електрону необхідна енергія . Відповідно коефіцієнт поверхневої іонізації, визначаючий вірогідність іонізації атомів на поверхні частинки плазми дорівнює:

, (9.14)

де gi, ga – статистична вага іонів і атомів відповідно;

- енергія активації десорбції іона.

Процес рекомбінації іона на поверхні частинки диму означає перехід електрона з рівня Фермі металу на вільний рівень валентного електрона іона, тобто енергія рекомбінації рівна . Відповідно коефіцієнт поверхневої рекомбінації рівний:

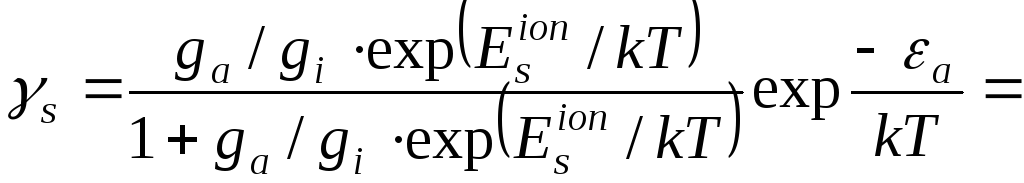
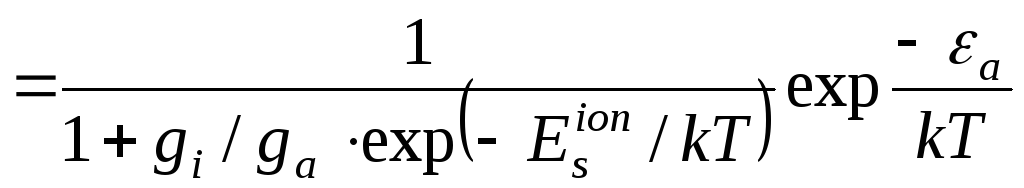, (9.15)

де - енергія активації десорбції атома.

Тепер, використовуючи вирази (9.14) і (9.15) можна визначити через суму потоків (9.11) ступінь іонізації атомів присадки у поверхні частинки диму (відоме як рівняння Саха - Ленгмюра):

. (9.16)

З рівнянь (9.13) і (9.16), одержуємо вираження для рівноважної поверхневої іонізації:

. (9.17)

Для визначення коефіцієнтів поверхневої іонізації і рекомбінації необхідно знати величини енергії активації десорбції іона і атома з поверхні частинки, які в даний час визначити не представляється можливим. Тому визначимо різницю в енергіях активації десорбції. Оскільки іон відрізняється від атома присадки тільки наявністю заряду, то різниця в енергіях активації десорбції визначиться величиною потенційного бар'єру на межі частинка – плазма .

_ Тоді рівняння іонізаційної рівноваги (9.17) можна представити в наступному вигляді:

, (9.18)

де параметр характеризує зміщення іонізаційної рівноваги біля поверхні частинки як за рахунок впливу об'ємного заряду плазми в поверхневому шарі () [147], так і властивостей поверхні розділу фаз ().

Розподіл потенціалу приймемо в наближенні Дебая. Тоді параметр нерівноважності дорівнює:

. (9.19)

Отже, поверхневе значення параметра нерівноважності дорівнює:

. (9.20)

Значення параметра нерівноважності визначає поверхневе значення квазінезбуреної концентрації . Відповідно, поверхневе значення електронної густини . Тоді рівняння (9.18) можна привести до вигляду:

.

Для випадку субмікронних частинок, коли, це рівняння можна спростити, до простого вираження . Звідси видно, що квазінезбурена концентрація може бути як менше, так і більше рівноважного значення, що визначається рівноважною концентрацією електронів біля поверхні частинки. Якщо, припустимо, значення роботи виходу і потенціалу іонізації такі, що рівняння (9.13) дає таке ж значення концентрації, що і рівняння Саха, то .

_Майже така ситуація реалізується для частинок алюмінію. Робота виходу електрона з алюмінію у вакуум рівна 3.74 eВ. Поправка на величину потенційного бар'єру на межі плазма – вакуум для цезію складає 0.6 eВ, тому робота виходу з алюмінію в плазму рівна eВ. В результаті, з рівняння (9.13) набуваємо значення поверхневої концентрації електронів. Рівняння Саха дає значення незбуреної концентрації , яке мало відрізняється від розрахованого по формулі (9.18) значення квазінезбуреної концентрації. Відповідно мале значення має параметр неравноважності . Таким чином, можливі випадки, коли частинки мало збурюють плазму, якщо їх параметри задовольняють рівноважному стану плазми.

Розглянемо випадки гранично малих і гранично великих концентрацій лужної домішки.

(а) При малих значеннях концентрації домішки рівняння (9.18) приводиться до вигляду:

. (9.21)

Як видно, величина потенційного бар'єру визначається відношенням концентрації електронів в поверхневому шарі до концентрації атомів домішки, що вводиться. При цьому частинка має великий позитивний заряд, оскільки . Беручи до уваги вираз (9.13), можна зробити висновок про те, що величина потенційного бар'єру більшою мірою визначається термоелектронною емісією, ніж іонізацією атомів домішки. Отже, заряд частинок також залежатиме, в основному, від поверхневих властивостей частинок, не дивлячись на те, що ступінь іонізації атомів домішкиу поверхні частинки, відповідна рівновазі в контакті, набагато більше одиниці. При малих значеннях концентрації атомів рівновага досягається за рахунок збільшення ступеня іонізації домішки.

_ (б) При великих значеннях концентрації домішкирівняння (9.18) можна перетворити до наступного вигляду:

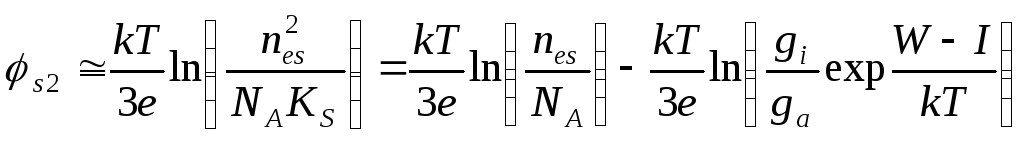. (9.22)

Відзначимо, що другий член в правій частині рівняння є виразом Саха - Ленгмюра, який описує рівноважну іонізацію атомів на електронейтральній поверхні металу. Дійсно, якщо слідує допустити, що то рівняння (9.22) приводиться до вигляду:

.

Звідси витікає, що при підвищенні концентрації атомів домішки в газовій фазі істотнішу роль в придбанні заряду частинкою грають процеси іонізації атомів і рекомбінації іонів на її поверхні з одночасним зниженням ролі термоелектронної емісії.

Результати розрахунку величини потенційного бар'єру на межі розподілу конденсованої фази з роботою виходу електрона з поверхні частинки = 4,7 еВ і газової плазми з присадкою атомів цезію при температурі 2000 К залежно від концентрації атомів домішки показані на рис.9. Конденсована фаза представлена сферичними частинками радіусом 3 мкм і концентрацією 10¹³ м^-3.

На графіках суцільна крива описує результати розрахунку, проведені по формулі (9.18), крапками позначена крива, розрахована по формулі (9.22), а пунктирна крива описує наближення малих концентрацій (9.21). Як видно, наближення низьких і високих значень концентрацій атомів достатньо добре співпадають з точним розрахунком у відповідних областях. При концентрації атомів порядка 10¹⁶ м^-3 величина потенційного бар'єру рівна нулю, що відповідає нейтральному заряду поверхні частинки.

На рис.10 приведені залежності середнього значення концентрації електронів, розраховані по моделі (крива 3), в якій не враховуються поверхневі процеси іонізації атомів і рекомбінації

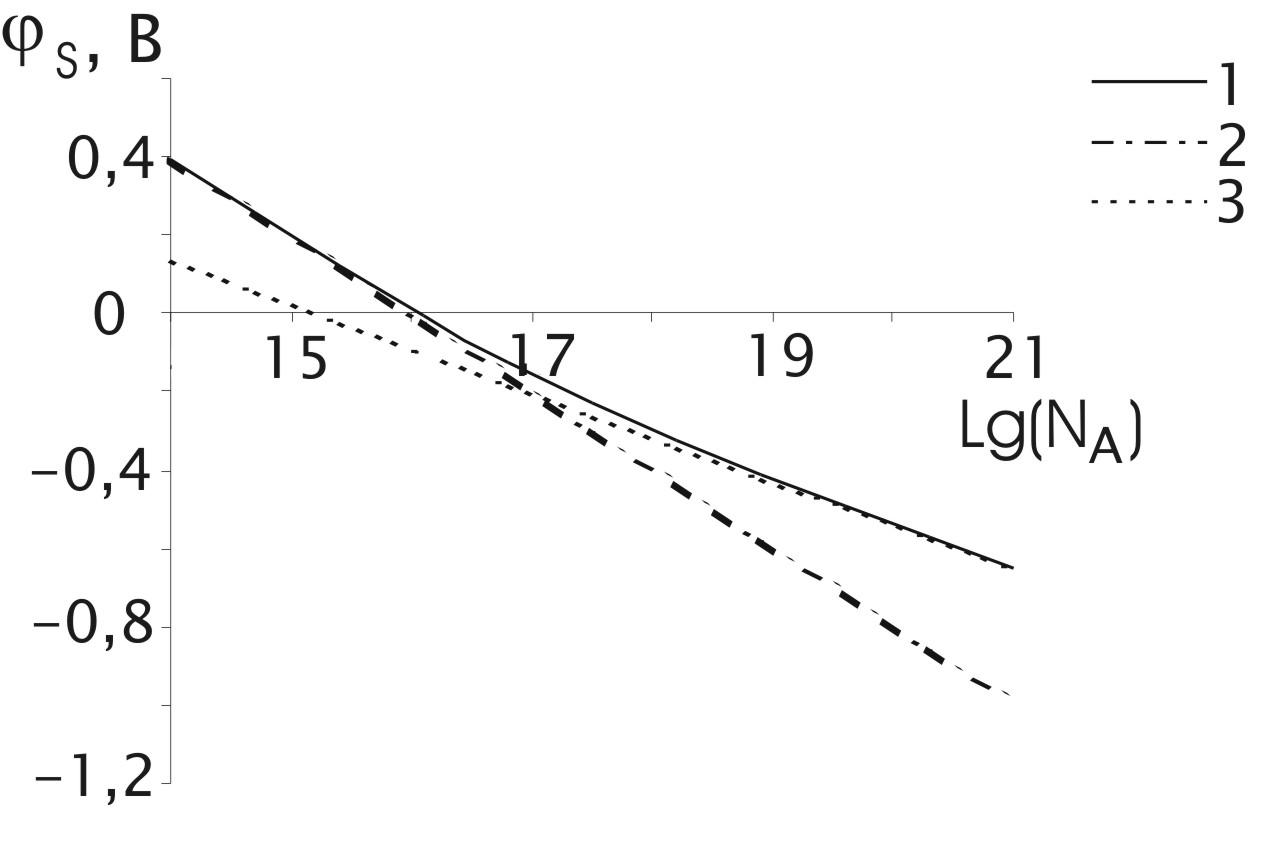
Рис.9. Залежність потенціалу поверхні частинки від концентрації домішки.

1 – загальний випадок;

2 – наближення малих концентрацій;

3 – наближення великих концентрацій.

іонів, і по представленій моделі (крива 2), а на рис.11 аналогічні залежності заряду частинок від концентрації атомів. Для порівняння на малюнку 10 показана залежність Саха (крива 1), що описує рівноважну іонізацію в газовій плазмі.

Як видно з графіків, обидві залежності, що описують іонізацію в пиловій плазмі, перетинають криву Саха, що відповідає нейтральному заряду частинок і із збільшенням концентрації атомів домішкиконцентрація електронів в пиловій плазмі стає нижче рівноважного значенні в аналогічній газовій плазмі. Відзначимо, що різні моделі дають різні результати. Урахування іонізаційно-рекомбінаційних процесів на поверхні частинок приводить до того, що частинки мають нейтральний заряд при вищих значеннях концентрації атомів.

рис 10. Залежність середнього значення концентрації електронів від

логарифма концентрації атомів цезію.

1 – розрахунок по рівнянню Саха;

2 - з урахуванням іонно - атомних процесів на поверхні частинки;

3 - з урахуванням тільки електронних процесів.

При низьких значеннях концентрації атомів іонізаційно - рекомбінаційні процеси на поверхні частинок приводять до істотнішої іонізації частинок, внаслідок чого підвищується концентрація вільних електронів і позитивний заряд частинок. Припускаючи постійність термоемісійного струму, можна зробити висновок про те, що зростання позитивного заряду частинок пов'язане з перенесенням позитивного заряду на частинку при рекомбінації іонів.

Очевидно, що рекомбінація іонів на поверхні частинок зміщує середній заряд частинок в позитивну сторону також і при великих концентраціях атомів.

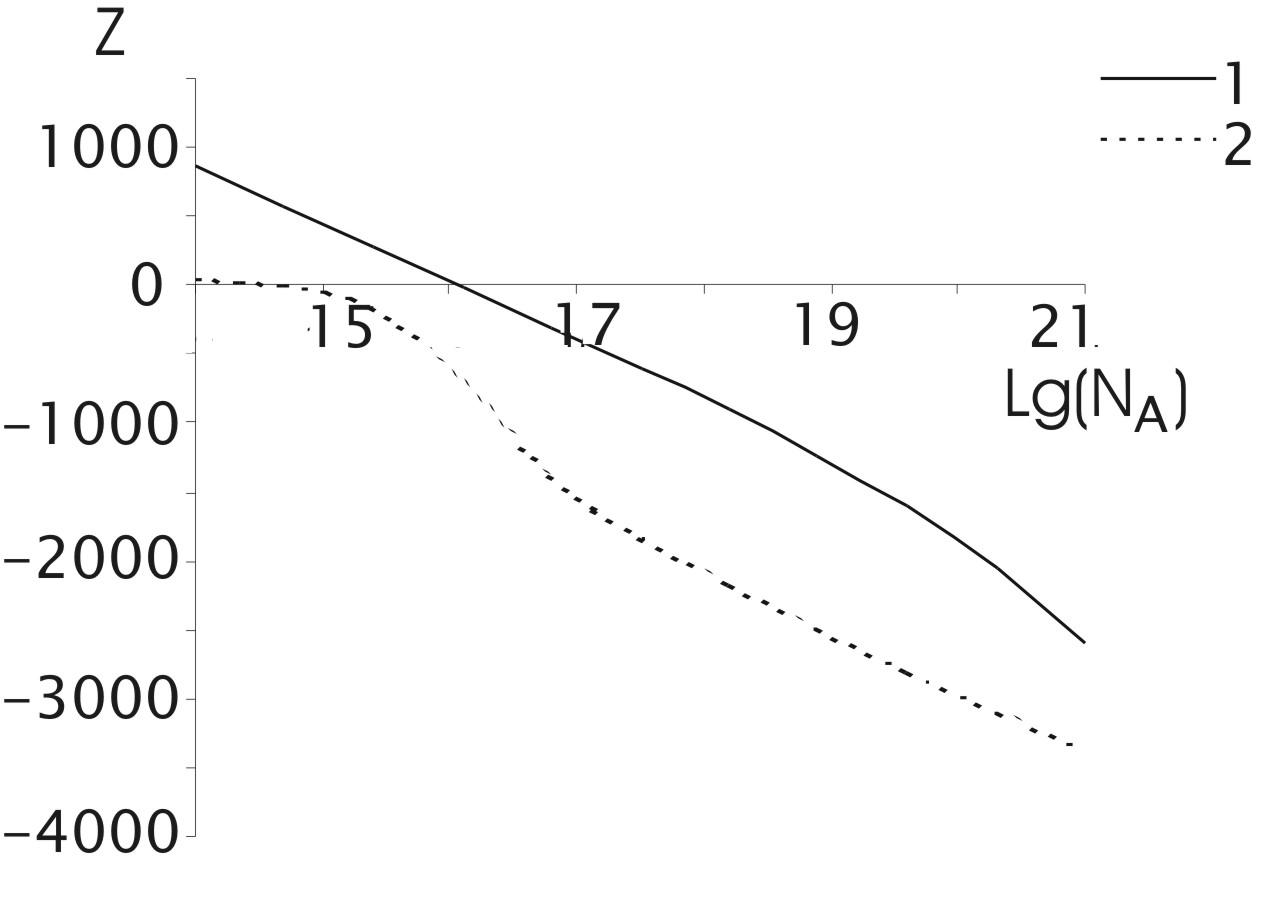
Рис. 11. Залежність середнього заряду частинок від логарифма концентрації атомів цезію.

1 – з урахуванням іонно - атомних процесів на поверхні частинки;

2 - з урахуванням тільки електронних процесів.

З іншого боку, при високих значеннях концентрації атомів ступінь іонізації домішки дуже низький і тому потік атомів на поверхню частинки істотно перевищить потік іонів. Тоді іонізація атомів на поверхні частинки могла б збільшити перенесення електронів на частинку. Проте, слід враховувати, що для поверхневої іонізації також як і для поверхневої рекомбінації іон і атом повинні мати деяку енергією активації, введення якої може змістити рівновагу на поверхні частинки, що приведе до зміни середнього заряду частинок і концентрації вільних електронів.

Таким чином, можна зробити висновок, що механізми придбання заряду поверхнею частинки залежать не тільки від поверхневих властивостей частинок, але і від таких характеристик навколишньої плазми, як її зарядний стан, ступінь іонізації і концентрація легкоіонізуючої домішки.