
- •Содержание
- •Задачи и упражнения
- •Задачи и упражнения
- •1. Найти приращение функции в произвольной точке , если приращение аргумента :
- •2. Используя определение производной функции, найти производные функций в произвольной точке :
- •3. Используя основные правила нахождения производных и таблицу производных, найти производные следующих функций:
Задачи и упражнения
1. Найти приращение функции в произвольной точке , если приращение аргумента :
1.1.
![]() ;
1.2.
;
1.2.
![]() ;
1.3.
;
1.3.
![]() ;
1.4.
;
1.4.
![]() .
.
2. Используя определение производной функции, найти производные функций в произвольной точке :
2.1.
![]() ;
2.2.
;
2.2.
![]() ;
2.3.
;
2.3.
![]() ;
2.4.
;
2.4.
![]() .
.
3. Используя основные правила нахождения производных и таблицу производных, найти производные следующих функций:
3.1.
![]() ;
3.2.
;
3.2.
![]() ;
3.3.
;
3.3.
![]() ;
;
3.4.
![]() ;
3.5.
;
3.5.
![]() ;
3.6.
;
3.6.
![]() ;
;
3.7.
 ;
3.8.
;
3.8.
![]() ;
3.9.
;
3.9.
![]() ;
;
3.10.
 ;
3.11.
;
3.11.
![]() ;
3.12.
;
3.12.
 ;
;
3.13.
![]() ;
3.14.
;
3.14.
![]() ;
3.15.
;
3.15.
![]() ;
;
3.16.
![]() ;
3.17.
;
3.17.
![]() ;
3.18.
;
3.18.
![]() ;
;
3.19.
![]() ;
3.20.
;
3.20.
![]() ;
3.21.
;
3.21.
![]() ;
;
3.22.![]() ;
3.23.
;
3.23.
![]() ;
3.24.
;
3.24.
![]() ;
;
3.25.
![]() ;
3.26.
;
3.26.
![]() ;
3.27.
;
3.27.
![]() ;
;
3.28.
 ;
3.29.
;
3.29.
 ;
3.30.
;
3.30.
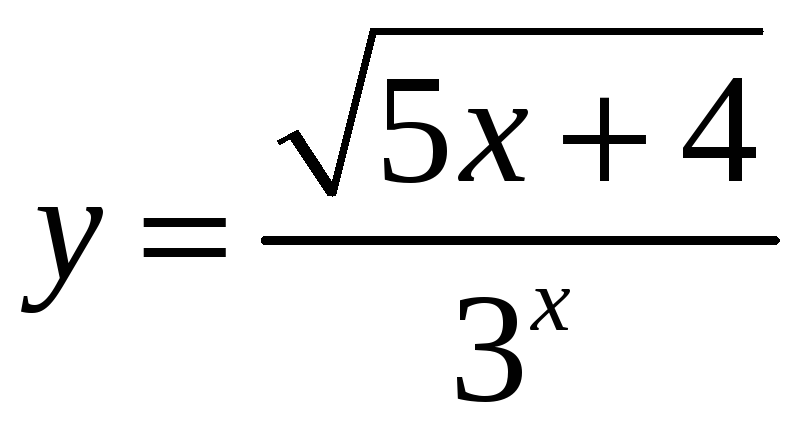 .
.
4. Найти
значение производной
![]() функции,
заданной неявно,
в точке
функции,
заданной неявно,
в точке
![]() :
:
4.1.
![]() ;
;
![]() ;
;
4.2.
 ;
;
![]() .
.
5. Найти
дифференциал
![]() функции
функции
![]() в точке с абсциссой
в точке с абсциссой
![]() :
:
5.1.
![]() ;
5.2.
;
5.2.
![]() ;
;
5.3.
![]() ;
5.4.
;
5.4.
![]() .
.
6. Найти производные второго порядка от следующих функций:
6.1.
![]() ;
6.2.
;
6.2.
![]() ;
6.3.
;
6.3.
![]() ;
6.4.
;
6.4.
![]() .
.
7. Найти
дифференциал второго порядка
![]() функции
функции
![]() в точке с абсциссой
в точке с абсциссой
![]() :
:
7.1.
![]() ;
7.2.
;
7.2.
![]() ,
,
![]() ;
;
7.3.
![]() .
.
8. Составить
уравнение касательной к графику функции
![]() в точке с абсциссой
в точке с абсциссой
![]() .
Построить в плоскости
.
Построить в плоскости
![]() кривую и касательную к ней.
кривую и касательную к ней.
8.1.
![]() ;
8.2.
;
8.2.
![]() ;
;
8.3.
![]() ;
8.4.
;
8.4.
![]() ;
;
8.5.
![]() ;
8.6.
;
8.6.
![]() .
.
9.
Используя
дифференциал первого порядка, найти
приближенное значение функции
![]() в точке
в точке
![]() .
.
9.1.
![]() ,
,
![]() ;
9.2.
;
9.2.
![]() ;
;
9.3.
![]() ;
9.4.
;
9.4.
![]() .
.
10. Вычислить пределы функций, используя правило Лопиталя.
10.1. ;
10.2.
;
10.2. ;
;
10.3. ;
10.4.
;
10.4. .
.
11. Исследовать
функцию
![]() на
монотонность и экстремумы.
на
монотонность и экстремумы.
11.1.![]() ;
11.2.
;
11.2.![]() ;
11.3.
;
11.3.![]() ;
11.4.
;
11.4.![]() ;
11.5.
;
11.5.![]() ;
11.6.
;
11.6.![]() ;
;
11.7.![]() ;
11.8.
;
11.8.![]() ;
11.9.
;
11.9.![]() ;
;
11.10.![]() ;
11.11.
;
11.11.![]() .
.
12. Найти интервалы выпуклости вверх и выпуклости вниз, точки перегиба графиков функций.
12.1. ;
12.2.
;
12.2.![]() ;
;
12.3.![]() ;
12.4.
;
12.4.
![]() .
.
13. Найти наименьшее и наибольшее значения функции на заданном промежутке. Решение проиллюстрировать графиком.
13.1.![]() ;
13.2.
;
13.2.![]() ;
;
13.3.![]() ;
13.4.
;
13.4.![]() .
.
14. Разложить
многочлен
![]() по натуральным степеням двучлена
по натуральным степеням двучлена
![]() по формуле Тейлора.
по формуле Тейлора.
15.
Представить функцию
![]() многочленом Тейлора второй степени в
окрестности
точки
многочленом Тейлора второй степени в
окрестности
точки
![]() .
.
16.
Представить функцию
![]() многочленом Тейлора второй степени в
окрестности точки
многочленом Тейлора второй степени в
окрестности точки
![]() .
Построить в одной системе координат
.
Построить в одной системе координат
![]() график данной функции и график полученного
многочлена Тейлора.
график данной функции и график полученного
многочлена Тейлора.
17. Провести полное исследование и построить графики следующих функций:
17.1.
![]() ;
17.2.
;
17.2.
 ;
17.3.
;
17.3.
![]() ;
;
17.4.
![]() ;
17.5.
;
17.5.
![]() ;
17.6.
;
17.6.
![]() ;
;
17.7.
 ;
17.8.
;
17.8.
 ;
17.9.
;
17.9.
 ;
;
17.10.
![]() ;
17.11.
;
17.11.
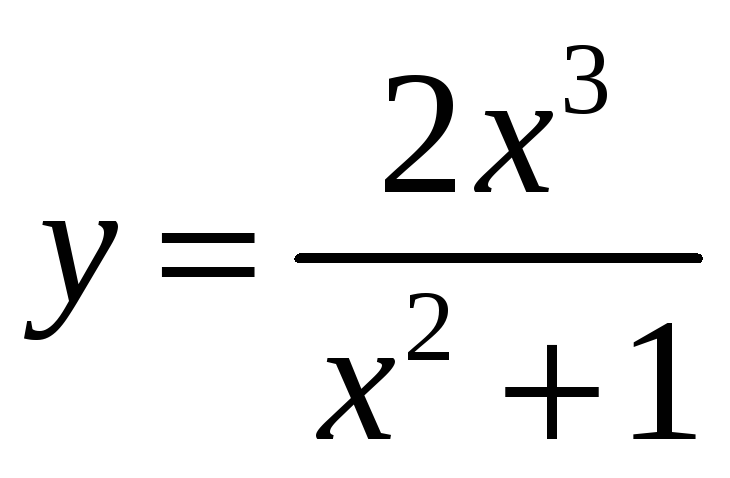 ;
17.12.
;
17.12.
![]() ;
;
17.13.
![]() ;
17.14.
;
17.14.
![]() ;
17.15.
;
17.15.
![]() ;
;
17.16.
![]() .
.
ОТВЕТЫ к задачам и упражнениям по теме «Производная»
1.1.
![]() ;
1.2.
;
1.2.
![]() ;
1.3.
;
1.3.
![]() ;
1.4.
;
1.4.
![]() ;
;
2.1.
![]() ;
2.2.
;
2.2.
![]() ;
2.3.
;
2.3.
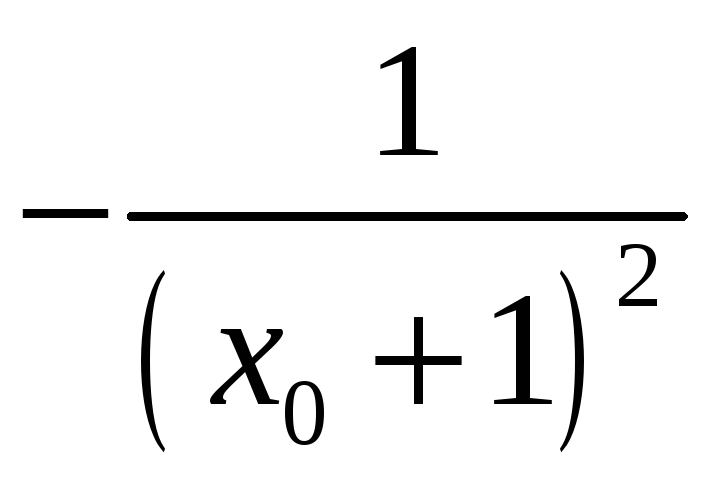 ;
2.4.
;
2.4.
 ;
;
3.1.
![]() ;
3.2.
;
3.2.
![]() ;
3.3.
;
3.3.
![]() ;
3.4.
;
3.4.
![]() ;
3.5.
;
3.5.
 ;
;
3.6.
 ;
3.7.
;
3.7.
 ;
3.8.
;
3.8.
![]() ;
3.9.
;
3.9.
![]() ;
;
3.10.
![]() ;
3.11.
;
3.11.
![]() ;
3.12.
;
3.12.
![]() ;
3.13.
;
3.13.
![]() ;
;
3.14.
![]() ;
3.15.
;
3.15.
![]() ;
3.16.
;
3.16.
![]() ;
3.17.
;
3.17.
![]() ;
;
3.18.
![]() ;
3.19.
;
3.19.
![]() ;
3.20.
;
3.20.
![]() ;
3.21.
;
3.21.
![]() ;
;
3.22.
![]() ;
3.23.
;
3.23.
![]() ;
3.24.
;
3.24.
 ;
3.25.
;
3.25.
 ;
;
3.26.
![]() ;
3.27.
;
3.27.
![]() ;
;
3.28.
 ;
3.29.
;
3.29.
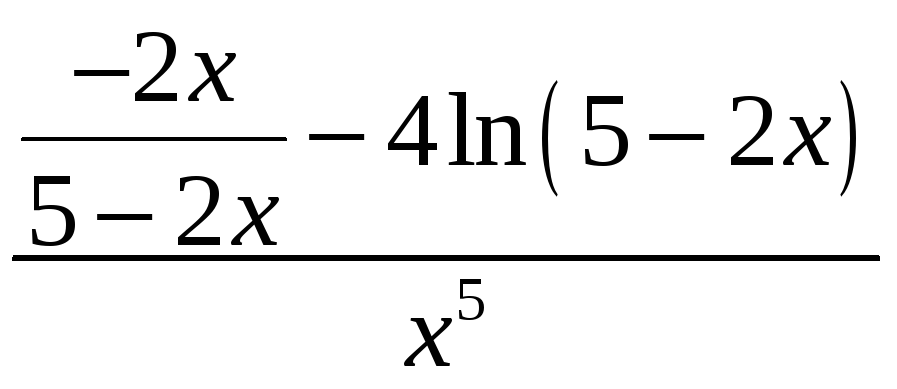 ;
;
3.30.
 ;
4.1.
;
4.1.
![]() ;
4.2.
;
4.2.
![]() ;
5.1.
;
5.1.
![]() ;
;
5.2.
![]() ;
5.3.
;
5.3.
![]() ;
5.4.
;
5.4.
![]() ;
6.1.
;
6.1.
![]() ;
6.2.
;
6.2.
![]() ;
6.3.
;
6.3.
 ;
6.4.
;
6.4.
![]() ;
;
7.1.
![]() ;
7.2.
;
7.2.
![]() ;
7.3.
;
7.3.
![]() ;
;
8.1.
![]() ;
8.2.
;
8.2.
![]() ;
8.3.
;
8.3.
![]() ;
8.4.
;
8.4.
![]() ;
8.5.
;
8.5.
![]() ;
;
8.6.
![]() ;
9.1.
;
9.1.
![]() ;
9.2.
;
9.2.
![]() ;
;
9.3.
![]() ;
9.4.
;
9.4.
![]() ;
10.1.
;
10.1.
![]() ;
10.2. 0; 10.3.
;
10.2. 0; 10.3.
![]() ;
;
10.4. 2;
11.1. возрастает
на
![]() ;
убывает на
;
убывает на
![]() ;
;
11.2. возрастает
на
![]() ;
убывает на
;
убывает на
![]() ;
;
![]() ;
;
11.3. возр.
на
![]() ;
убыв, на
;
убыв, на![]() ;
11.4.
возрастает на
;
11.4.
возрастает на
![]() ;
;
убывает на
![]() ;
;
11.5. убывает
на
![]() ;
экстремумов нет; 11.6.
возрастает
на
;
экстремумов нет; 11.6.
возрастает
на
![]() ;
убывает на
;
убывает на
![]() ;
;
![]() ;
11.7. убывает
на
;
11.7. убывает
на
![]() ;
экстремумов нет; 11.8.
возр. на
;
экстремумов нет; 11.8.
возр. на
![]() ;
убыв. на
;
убыв. на
![]() ;
экстремумов нет; 11.9.
возрастает
на
;
экстремумов нет; 11.9.
возрастает
на
![]() ;
экстремумов нет;
;
экстремумов нет;
11.10. возрастает
на
![]() ;
убывает на
;
убывает на
![]() ;
;
 ;
;
11.11. возрастает
на
![]() ;
убывает на
;
убывает на
![]() ;
;
![]() ;
;
12.1. график
функции направлен выпуклостью вверх
на
![]() ;
выпуклостью вниз на
;
выпуклостью вниз на
![]() ;
точка перегиба
;
точка перегиба
 ;
12.2. график
функции направлен выпуклостью вверх
на
;
12.2. график
функции направлен выпуклостью вверх
на
![]() ;
выпуклостью вниз на
;
выпуклостью вниз на
![]() ;
точка перегиба
;
точка перегиба
![]() ;
точка перегиба
;
точка перегиба
![]() ;
;
12.3. график
функции направлен выпуклостью вверх
на
![]() ;
выпуклостью вниз на
;
выпуклостью вниз на
![]() ;
точек перегиба
нет;
;
точек перегиба
нет;
12.4. график
функции направлен выпуклостью вверх
на
![]() ;
точек перегиба
нет;
;
точек перегиба
нет;
13.1.![]() ;
;
13.2.![]() ;
;
13.3.![]() ;
13.4.
;
13.4.![]() ;
;
14.
![]() ;
15.
;
15.
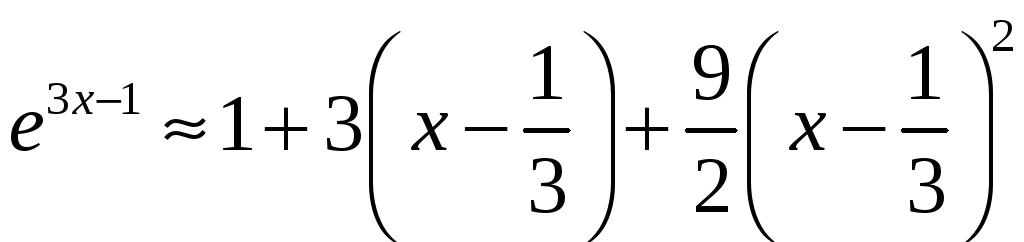
16.
![]() .
.
КОНТРОЛЬНОЕ ЗАДАНИЕ по теме «Производная»
1. Используя
определение производной функции, найти
производную функции
![]() в
точке
в
точке
![]() ,
(
,
(![]() -
произвольная точка области определе -
ния функции).
-
произвольная точка области определе -
ния функции).
2. Используя основные правила нахождения производных и таблицу производных, найти производные следующих функций:
2.1.![]() ;
2.2.
;
2.2.![]() ;
2.3.
;
2.3. .
.
3. Найти дифференциал первого и второго порядка
функции
![]() в точке
в точке
![]() .
.
4. Составить
уравнение касательной к графику функции
![]()
в точке
![]() .
Построить в плоскости
.
Построить в плоскости
![]() кривую и касательную к ней.
кривую и касательную к ней.
5. Используя
дифференциал первого порядка, найти
приближенное значение
![]() .
.
6. Вычислить предел функции, используя правило Лопиталя.
6.1.
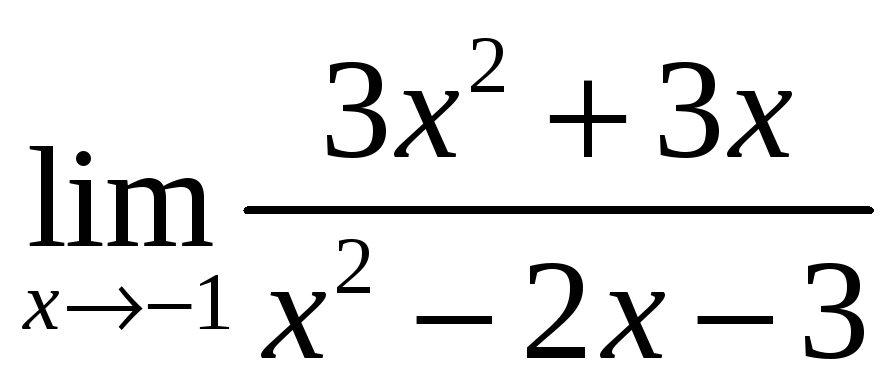 ;
6.2.
;
6.2.
 .
.
7. Исследовать
функцию
![]() на монотонность и экстремумы.
на монотонность и экстремумы.
8. Найти
интервалы выпуклости вверх, выпуклости
вниз и точки перегиба функции
![]() .
.
9. Найти
наибольшее и наименьшее значения функции
![]() на отрезке
на отрезке
![]() .
.
10. Представить
функцию
![]() многочленом Тейлора второй степени в
окрестности точки
многочленом Тейлора второй степени в
окрестности точки
![]() .
Построить в одной системе координат
.
Построить в одной системе координат
![]() график данной функции и график полученного
многочлена Тейлора.
график данной функции и график полученного
многочлена Тейлора.
11. Провести полное исследование функции и построить ее график.
11.1.
![]() ;
11.2.
;
11.2.
![]() ;
11.3.
;
11.3.
![]() .
.
ОТВЕТЫ к контрольному заданию по теме «Производная»
1.![]() ;
2.1.
;
2.1.
 ;
2.2.
;
2.2.![]() ;
;
2.3.
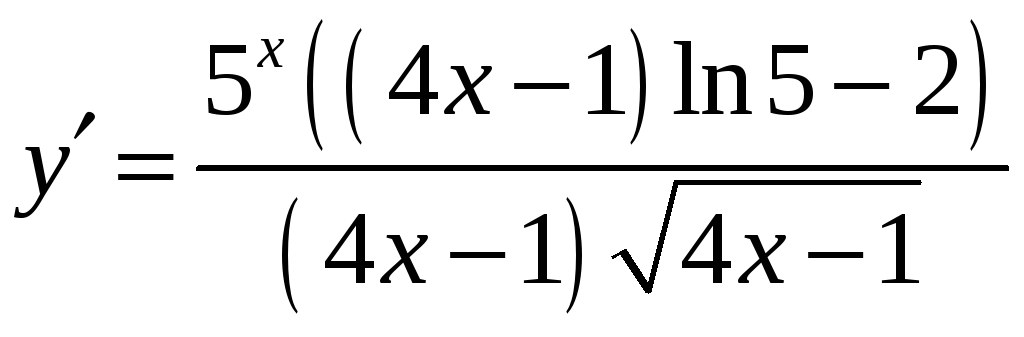 ;
;
3.
![]() ;
4.
;
4.
![]() ;
5.
;
5.
![]() ;
;
6.1. 0,75;
6.2. 1;
7. возрастает
на
![]() ;
;
убывает на
![]() ;
;
![]() ;
8. график
функции направлен выпуклостью вверх
на
;
8. график
функции направлен выпуклостью вверх
на
![]() ;
выпуклостью
вниз на
;
выпуклостью
вниз на
![]() ;
;
точка перегиба
![]() ;
9.
;
9.
![]() ;
;
![]() ;
;
10.
![]() .
.
ТЕСТ по теме «Производная»
К каждому их предложенных ниже заданий дано четыре варианта ответов. Один из предложенных ответов – правильный.
Выбрать правильный ответ.
В заданиях 1; 2 найти производную функции:
1.
![]() .
.
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
2.
![]() .
.
Варианты ответов:
а) ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.
В заданиях 3;
4 найти
значение производной функции
![]() в точке
в точке
![]() :
:
3.
![]() в точке
в точке
![]() .
.
Варианты ответов:
а) 1;
б)
![]() ;
в)
;
в)
![]() ;
г)
2.
;
г)
2.
4.
![]() в точке
в точке
![]() .
.
Варианты ответов:
а) 0,2;
б)
1; в)
1,2; г)
![]() .
.
5. Найти
дифференциал функции
 в точке
в точке
![]() .
.
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
0; г)
не существует.
;
в)
0; г)
не существует.
6. Составить
уравнение касательной к графику функции
![]() в точке
в точке
![]() .
.
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
7. Найти
интервалы, на которых функция
![]() монотонно убывает.
монотонно убывает.
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
8. Найти
абсциссу точки максимума функции
![]() .
.
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
1;
г)
;
в)
1;
г)
![]() .
.
9.
При каком значении параметра а график
функции
![]() имеет перегиб при
имеет перегиб при
![]() ?
?
Варианты ответов:
а)
![]() ;
б)
3;
в) 2;
г)
;
б)
3;
в) 2;
г)
![]() .
.
В заданиях 10; 11 вычислить предел функции, используя правило Лопиталя:
10.
 .
.
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
0;
г)
;
в)
0;
г)
![]() .
.
11.
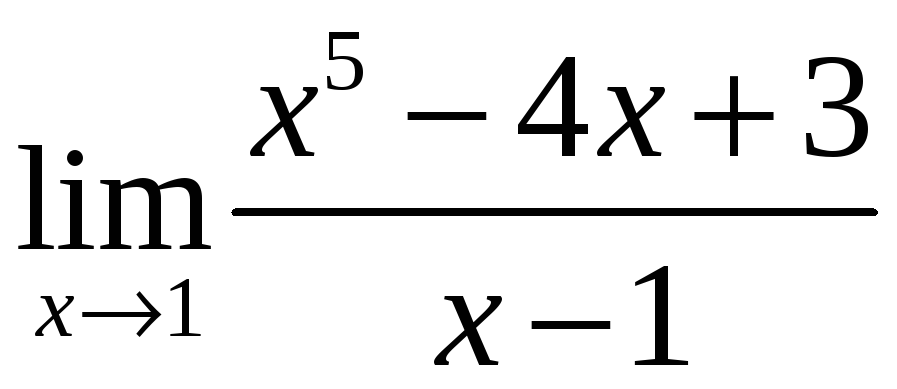 .
.
Варианты ответов:
а) 1;
б)
![]() ;
в)
;
в)
![]() ;
г)
5.
;
г)
5.
Правильный ответ:
1.
![]() ;
2.
;
2.
 ;
3.
;
3.
![]() ;
;
4. 1,2;
5.
![]() ;
6.
;
6.
![]() ;
;
7.
![]() ;
8.
;
8.
![]() ;
9.
;
9.
![]() ;
;
10.
![]() ;
11.
1.
;
11.
1.
